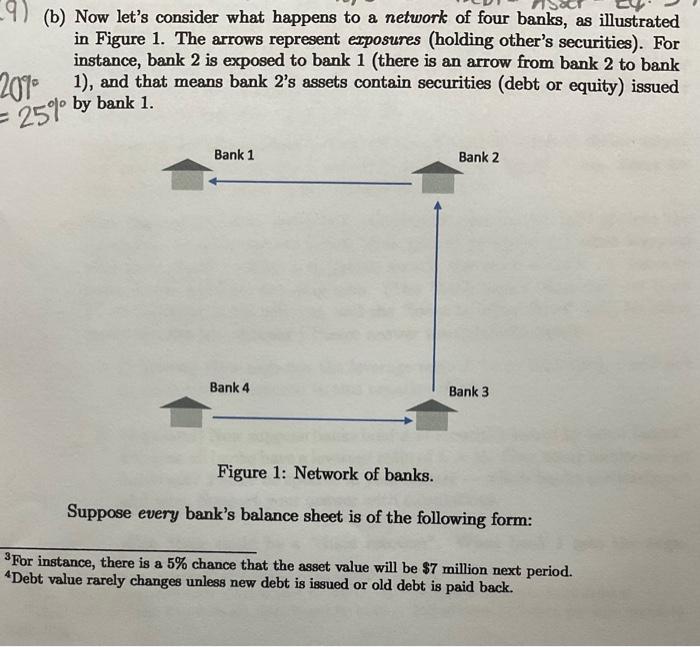
(b) Now let's consider what happens to a network of four banks, as illustrated in Figure 1. The arrows represent exposures (holding other's securities). For instance, bank 2 is exposed to bank 1 (there is an arrow from bank 2 to bank 1), and that means bank 2's assets contain securities (debt or equity) issued 25 by bank 1. Figure 1: Network of banks. Suppose every bank's balance sheet is of the following form: 3For instance, there is a 5% chance that the asset value will be $7 million next period. 4 Debt value rarely changes unless new debt is issued or old debt is paid back. That is, 80% of bank 2 's asoets are securities issued by bank 1 , and the remaining 20% are loons made to other firms (non-banks). This immediately implies that the bealth of bank 1 impacts bank 2 . If bank 1 goes bankrupt, the securitics (debt or equity) issued by benk 1 may go down in value, which will lead bank 2 to also suffer a loss in its assets, which may then trigger bank 2 to go benkrupt as well. Recall how investors are paid in bankruptcy. 5 if a bank goes bankrupt, then its equity becomes worthless, and its debt bolders get all remaining asset valwe with a possble "haircut". For ingtance, suppose a bank has leverage L=10 (so equity is 1/L=1/10=10% of total assets). Suppose the bunk's asset value declines by 30%, so it goes bankrupt, its equity becomes worthless, and its debt is now worth 90h14y=27 as much as before. 6 So the holders of the bank's equity suffer a loes of 100% (all lostl), and the holders of its debt suffer a proportional loes of 197=92 22.2%. Suggestion: for all questions below, you don't need to think in dollar vulaes, but only noed to think about vulues in proportional terms - e-g. loans are 20% of total asect value, in the balance sheet above. Now that we nre done describing background information, let's go into the questions. In all questions beiow, your goal is to figure out what heppens after (only) bank 1 suffers a negative shock: the value of bank 1 's "loans to other firme" saddenly becomes zero. (The "bank-issued socurities" on bank 1 balance shoet is not affected, and the "loans to other firms" held by other benks are alio not affected.) Please answer the questions below. i. ( 1 point) How high can the leverige ratio L be so that baink 1 will not go bankrupt in responae to this negative shock? i1. (2 points) Now suppose banks hold debt socurities insued by other banks? 7 Suppose all banks bave a leverage ratio of L=15. How many banks will go banlcrupt? Please be specific in your antower - which banks are bankrupt and why. Support your answer with calculations. Hint. there conld be a "chain reaction". When bank 1 gets the nera- SYou tikely have enconstered thin biefly in an asoounting elass. "The 70% of rennining smet value in used to pyy the debt holdern in a peoportional frahion. bank 2 , ete. (b) Now let's consider what happens to a network of four banks, as illustrated in Figure 1. The arrows represent exposures (holding other's securities). For instance, bank 2 is exposed to bank 1 (there is an arrow from bank 2 to bank 1), and that means bank 2's assets contain securities (debt or equity) issued 25 by bank 1. Figure 1: Network of banks. Suppose every bank's balance sheet is of the following form: 3For instance, there is a 5% chance that the asset value will be $7 million next period. 4 Debt value rarely changes unless new debt is issued or old debt is paid back. That is, 80% of bank 2 's asoets are securities issued by bank 1 , and the remaining 20% are loons made to other firms (non-banks). This immediately implies that the bealth of bank 1 impacts bank 2 . If bank 1 goes bankrupt, the securitics (debt or equity) issued by benk 1 may go down in value, which will lead bank 2 to also suffer a loss in its assets, which may then trigger bank 2 to go benkrupt as well. Recall how investors are paid in bankruptcy. 5 if a bank goes bankrupt, then its equity becomes worthless, and its debt bolders get all remaining asset valwe with a possble "haircut". For ingtance, suppose a bank has leverage L=10 (so equity is 1/L=1/10=10% of total assets). Suppose the bunk's asset value declines by 30%, so it goes bankrupt, its equity becomes worthless, and its debt is now worth 90h14y=27 as much as before. 6 So the holders of the bank's equity suffer a loes of 100% (all lostl), and the holders of its debt suffer a proportional loes of 197=92 22.2%. Suggestion: for all questions below, you don't need to think in dollar vulaes, but only noed to think about vulues in proportional terms - e-g. loans are 20% of total asect value, in the balance sheet above. Now that we nre done describing background information, let's go into the questions. In all questions beiow, your goal is to figure out what heppens after (only) bank 1 suffers a negative shock: the value of bank 1 's "loans to other firme" saddenly becomes zero. (The "bank-issued socurities" on bank 1 balance shoet is not affected, and the "loans to other firms" held by other benks are alio not affected.) Please answer the questions below. i. ( 1 point) How high can the leverige ratio L be so that baink 1 will not go bankrupt in responae to this negative shock? i1. (2 points) Now suppose banks hold debt socurities insued by other banks? 7 Suppose all banks bave a leverage ratio of L=15. How many banks will go banlcrupt? Please be specific in your antower - which banks are bankrupt and why. Support your answer with calculations. Hint. there conld be a "chain reaction". When bank 1 gets the nera- SYou tikely have enconstered thin biefly in an asoounting elass. "The 70% of rennining smet value in used to pyy the debt holdern in a peoportional frahion. bank 2 , ete