Background Facts

This information is to provide context for your data analysis and recommendations. Consider your group to be a team of consultants hired by Organix Cereals to analyze the data provided and report your findings formally to the company.

Company: Organix Cereals (a fictional company) is a small producer of specialty organic breakfast cereal. Its signature product is Gluten-Free Organic Crispies, sold directly online to consumers. The company sells approximately 4 million boxes annually.

Box label weight: 623 grams

Price per box: $6.00

Cost of goods sold (per box): $4.00 (based on historical mean weight of 625 grams)

Company Standards: In the automated packaging process, equipment is set to fill boxes with a mean weight of 625 grams and a standard deviation of 6 grams. This is the company standard for the box weights. As a small, independent producer of breakfast cereals, Organix uses older equipment and technology in its packaging process. Accordingly, the process results in boxes that are not always packed with exactly 623 grams (weight stated on the label).

The company sets the equipment to a target weight slightly higher than the weight stated on the box label to avoid penalties imposed by government inspectors if the box weights do not meet the government standards, and to ensure that customers receive the amount of cereal for which they pay. This is a common industry practice.

Government Standards: Failure to meet government standards can result in fines of $200,000 or more, litigation, and negative publicity for the company and its brand. The government is not concerned if the company is overfilling boxes.

1.Penalties can be assessed against a company when any individual package weighs less than the Maximum Allowable Variation (MAV). The Maximum Allowable Variation (MAV) is the limit of reasonable variation for an individual package based on the NIST Handbook 133.The MAV is 23.5 grams below the declared box label weight of 623 grams. The lowest allowable weight, LMAV, is found by taking the label weight minus the MAV.

2.The company can also be penalized if the average package weight does not at least meet the declared box label weight of 623 grams.

Data: The company recently took a random sample of 500 boxes of their signature cereal and measured their exact weights. The goals of this internal audit were to determine whether (1.) the company is meeting the targets set by management, and (2.) the company is in compliance with government regulations. The data that resulted from this sample can be found on the Excel workbook labeled Capstone Project Data SS2021.

Analysis: Three templates are provided to guide your analysis. Your group must submit all three completed templates along with the final report in BlackBoard. The questions in the templates include the minimum requirements for your analysis in this project. Your group may choose to do additional statistical and business analysis beyond the minimum requirements in the templates.

For Template 1, you will use the data on the tab labeled Cereal Weights. This data will also be used for the first part of Template 2. Also for Template 2 you will use data found on the tab labeled Weights after Adjustment. For Template 3 you will use the data found on the tab labeled Weights and Speeds.

As you perform your calculations, continue to round data to four decimal places.

I need help with how to describe: I solved the above table.

1. Does the data contain any outliers? If yes, should those outliers be left in the data set for analysis or removed? Explain.

2. Using Excel, create and insert a frequency distribution and histogram of the box weights. Use 10 classes to build the frequency distribution.

3. Based on (a.) the descriptive statistics, (b.) the histogram, and (c.) the empirical rule, does it appear that the box weights follow a normal distribution with a symmetric bell-shaped curve? Justify your response with your data analysis.

4. Assuming the package weights are normally distributed, convert the MAV value to a z-score using the formula z = (LMAV mean)/standard deviation. What is the probability that any individual package weight will fall below the LMAV of 599.5 grams? Does this pose a risk to the company?

5. Based on your analysis, should management have any concerns about the packaging process being out of compliance with the government standards? Explain

6. Based on your analysis, should management have any concerns about the packaging process from a business perspective? Explain.

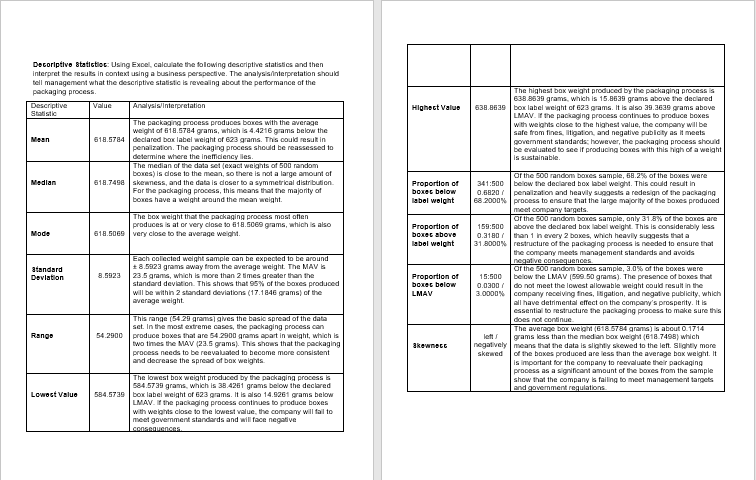
Highest Value Decoriptivo Staticos: Using Excel, calculate the folowing descriptive statistics and then Interpret the results in context using a business perspective. The analysis interpretation should tell management what the descriptive statistic is revealing about the performance of the packaging process. Descriptive Value Analysis interpretation Statistic The packaging process produces boxes with the average weight of 618.5784 grams, which is 4.4216 grams below the Mean 618.5784 declared box label weight of 623 grams. This could result in penalization. The packaging process should be reassessed to determine where the inefficiency lies. The median of the data set (exact weights of 500 random boxes) is dose to the mean, so there is not a large amount of Median 618.7490 skewness, and the data is doser to a symmetrical distribution For the packaging process, this means that the majority of boxes have a weight around the mean weight The box weight that the packaging process most often produces is at or very close to 618.5069 grams, which is also Mode 618.506 very close to the average weight. The highest box weight produced by the packaging process is 638.8639 grams which is 15.8639 grams above the declared 638.8636 box label weight of 623 grams. It is also 29.3636 grams above LMAV. I the packaging process continues to produce boxes with weights close to the highest value, the company will be safe from fines litigation and negative publicity as it meets government standards: however, the packaging process should be evaluated to see if producing boxes with this high of a weight is sustainable Proportion of boxes below label weight Proportion of boxes above label wolght Standard Dovlation Proportion of boxec below LMAV or the 500 random bones sample, 68.2% of the boxes were 341:500 below the declared box label weight. This could result in 0.68201 penalization and heavily suggests a redesign of the packaging 68 2000% process to ensure that the large majority of the boxes produced meet company targets. or the 500 random bones sample, only 31.8% of the boxes are 159:500 above the declared box label weight. This is considerably less 0.31807 than 1 in every 2 boxes, which heavily suggests that a 31.8000% restructure of the packaging process is needed to ensure that the company meets management standards and avoids negative consequences or the 500 random bones sample, 3.0% of the boxes were 15:500 below the LMAV 599 50 grams). The presence of boxes that 0.0300/ do not meet the lowest allowable weight could result in the 3.0000% company receiving fines, Itigation, and negative publicity, which all have detrimental effect on the comparw's prosperity. It is essential to restructure the packaging process to make sure this does not continue The average box weight (618_5784 gram) is about 0.1714 left grams less than the median box weight (618.7498) which negatively means that the data is slightly skewed to the left. Slightly more skewed of the boxes produced are less than the average box weight. It is important for the company to reevaluate their packaging process as a significant amount of the boxes from the sample show that the company is failing to meet management targets and government regulations Each collected weight sample can be expected to be around + 8.5923 grams away from the average weight. The MAVIS 8.5923 23.5 grams, which is more than 2 times greater than the standard deviation. This shows that 95% of the boxes produced will be within 2 standard deviations (17.1846 grams) of the average weight This range (54 29 grams gives the basic spread of the data set. In the most extreme cases, the packaging process can 54.2900 produce boxes that are 54.2900 grams apart in weight, which is two times the MAV (23.5 grams). This shows that the packaging process needs to be reevaluated to become more consistent and decrease the spread of box weights. The lowest box weight produced by the packaging process is 584.5739 grams which is 38.4261 grams below the declared 584.573 box label weight of 623 grams. It is also 14.5261 grams below LMAV. If the packaging process continues to produce boxes with weights close to the lowest value, the company will fail to meet government standards and will face negative CASA Range Skewnect Lowoct Value Highest Value Decoriptivo Staticos: Using Excel, calculate the folowing descriptive statistics and then Interpret the results in context using a business perspective. The analysis interpretation should tell management what the descriptive statistic is revealing about the performance of the packaging process. Descriptive Value Analysis interpretation Statistic The packaging process produces boxes with the average weight of 618.5784 grams, which is 4.4216 grams below the Mean 618.5784 declared box label weight of 623 grams. This could result in penalization. The packaging process should be reassessed to determine where the inefficiency lies. The median of the data set (exact weights of 500 random boxes) is dose to the mean, so there is not a large amount of Median 618.7490 skewness, and the data is doser to a symmetrical distribution For the packaging process, this means that the majority of boxes have a weight around the mean weight The box weight that the packaging process most often produces is at or very close to 618.5069 grams, which is also Mode 618.506 very close to the average weight. The highest box weight produced by the packaging process is 638.8639 grams which is 15.8639 grams above the declared 638.8636 box label weight of 623 grams. It is also 29.3636 grams above LMAV. I the packaging process continues to produce boxes with weights close to the highest value, the company will be safe from fines litigation and negative publicity as it meets government standards: however, the packaging process should be evaluated to see if producing boxes with this high of a weight is sustainable Proportion of boxes below label weight Proportion of boxes above label wolght Standard Dovlation Proportion of boxec below LMAV or the 500 random bones sample, 68.2% of the boxes were 341:500 below the declared box label weight. This could result in 0.68201 penalization and heavily suggests a redesign of the packaging 68 2000% process to ensure that the large majority of the boxes produced meet company targets. or the 500 random bones sample, only 31.8% of the boxes are 159:500 above the declared box label weight. This is considerably less 0.31807 than 1 in every 2 boxes, which heavily suggests that a 31.8000% restructure of the packaging process is needed to ensure that the company meets management standards and avoids negative consequences or the 500 random bones sample, 3.0% of the boxes were 15:500 below the LMAV 599 50 grams). The presence of boxes that 0.0300/ do not meet the lowest allowable weight could result in the 3.0000% company receiving fines, Itigation, and negative publicity, which all have detrimental effect on the comparw's prosperity. It is essential to restructure the packaging process to make sure this does not continue The average box weight (618_5784 gram) is about 0.1714 left grams less than the median box weight (618.7498) which negatively means that the data is slightly skewed to the left. Slightly more skewed of the boxes produced are less than the average box weight. It is important for the company to reevaluate their packaging process as a significant amount of the boxes from the sample show that the company is failing to meet management targets and government regulations Each collected weight sample can be expected to be around + 8.5923 grams away from the average weight. The MAVIS 8.5923 23.5 grams, which is more than 2 times greater than the standard deviation. This shows that 95% of the boxes produced will be within 2 standard deviations (17.1846 grams) of the average weight This range (54 29 grams gives the basic spread of the data set. In the most extreme cases, the packaging process can 54.2900 produce boxes that are 54.2900 grams apart in weight, which is two times the MAV (23.5 grams). This shows that the packaging process needs to be reevaluated to become more consistent and decrease the spread of box weights. The lowest box weight produced by the packaging process is 584.5739 grams which is 38.4261 grams below the declared 584.573 box label weight of 623 grams. It is also 14.5261 grams below LMAV. If the packaging process continues to produce boxes with weights close to the lowest value, the company will fail to meet government standards and will face negative CASA Range Skewnect Lowoct Value