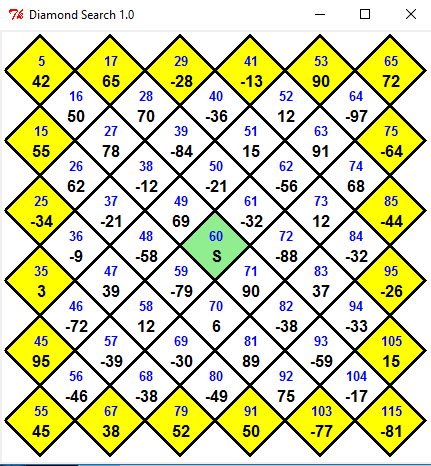
Background: Finding the lowest cost path through a graph is a common challenge in many applications. While it can be an expensive process in general, often constraints of the graph structure simplify the search. In this project, well examine exiting a diamond grid (shown tilted 45 degrees counterclockwise below). The weights between points are randomly generated integers between -99 and 99, inclusive. Non-participating array cells (the padding) have weights set to 10,000. Note that the linearized array offset is shown in blue in each square. The goal is to find the minimum cost path between the center and any exit edge where cost is the sum of all weights encountered along the path. All paths must have a length of five squares not counting the center square. The problem is considerably more difficult if this path requirement is relaxed.

Strategy: Unlike many function only programming tasks where a solution can be quickly envisioned and implemented, this task requires a different strategy.

Before writing any code, reflect on the task requirements and constraints. Mentally explore different approaches and algorithms, considering their potential performance and costs. The metrics of merit are static code length, dynamic execution time, and storage requirements. There are often trade offs between these parameters. Sometimes back of the envelope calculations (e.g., how many comparisons will be performed) can help illuminate the potential of an approach.

the following is the Shell COde

/* D i a m o n d S e a r c h Student Name:Surafel Argaw Date: Feb 14 2017

ECE 2035 Project 1-1

This program finds the shortest path out of a diamond of weighted squares. */

#include #include

/* Example from Project description: int Array[121] = { 10000, 10000, 10000, 10000, 10000, -99, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, -49, -37, 83, 10000, 10000, 10000, 10000, 10000, 10000, 10000, -64, 19, 67, -82, -2, 10000, 10000, 10000, 10000, 10000, -30, -37, 64, -68, 92, 40, 2, 10000, 10000, 10000, 27, -70, 52, 79, -77, -31, -41, -77, -81, 10000, 80, -73, -8, -59, 53, 0, -47, 46, -32, 98, -98, 10000, 13, -99, -47, -60, -14, -45, 80, 15, 69, 10000, 10000, 10000, -9, 8, -88, 69, 54, 12, 53, 10000, 10000, 10000, 10000, 10000, -21, 3, -61, -43, 29, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 45, -34, -85, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 59, 10000, 10000, 10000, 10000, 10000 }; */

#define ArraySize 121

int main(int argc, char *argv[]) { int Array[ArraySize]; int Length, MinCost = 10000; int Load_Mem(char *, int *);

if (argc != 2) { printf("usage: P1-1 valuefile "); exit(1); } Length = Load_Mem(argv[1], Array); if (Length != ArraySize) { printf("valuefile does not contain valid data. "); exit(1); }

/* Your diamond search code goes here */

int a=0; int b=0; int col=0; int row=0; int c=0; int cj=0; int ck=0; int cost[121]; for(a=0; a=10000) cost[a]=0; b=((row+1)*11)+col; c=(row*11)+(col+1); cj=cost[a]+Array[b]; ck=cost[a]+Array[c];

printf("cost Mat-> cur:(%d,%d):[%d], row+1: [%d], col+1: [%d] ",row,col, cost[a],cj,ck );

if (cjcost[u]) MinCost=cost[u]; else MinCost=MinCost; } /* include this print statement. */ printf("The shortest path cost is [%d] ", MinCost); return 0; printf(" "); printf(" "); }

/* This routine loads in up to ArraySize newline delimited integers from a named file in the local directory. The values are placed in the passed integer array. The number of input integers is returned. */

int Load_Mem(char *InputFileName, int IntArray[]) { int N, Addr, Value, NumVals; FILE *FP;

FP = fopen(InputFileName, "r"); if (FP == NULL) { printf("%s could not be opened; check the filename ", InputFileName); return 0; } else { for (N=0; N

the second picture is the Shell code for the C programming

Diamond Search 1.0 29 53 65 -28 -13 90 72 42 52 64 28 40 70 -36 97 50 75 27 39 51 -84 15 91 -64 55 78 50 74 26 38 62 -1 21 -56 68 37 49 61 73 25 -34 21 69 -32 12 84 36 48 -88 -32 -58 71 83 95 35 47 59 -79 90 37 -26 39 70 82 94 46 58 -38 -33 -72 105 69 81 93 -39 -30 89 -59 1 95 104 92 56 68 -46 -38 -49 75 -17 103 115 55 67 79 52 50 77 -81 45 38 5 32 71 19 2 82 16 26 15 Diamond Search 1.0 29 53 65 -28 -13 90 72 42 52 64 28 40 70 -36 97 50 75 27 39 51 -84 15 91 -64 55 78 50 74 26 38 62 -1 21 -56 68 37 49 61 73 25 -34 21 69 -32 12 84 36 48 -88 -32 -58 71 83 95 35 47 59 -79 90 37 -26 39 70 82 94 46 58 -38 -33 -72 105 69 81 93 -39 -30 89 -59 1 95 104 92 56 68 -46 -38 -49 75 -17 103 115 55 67 79 52 50 77 -81 45 38 5 32 71 19 2 82 16 26 15