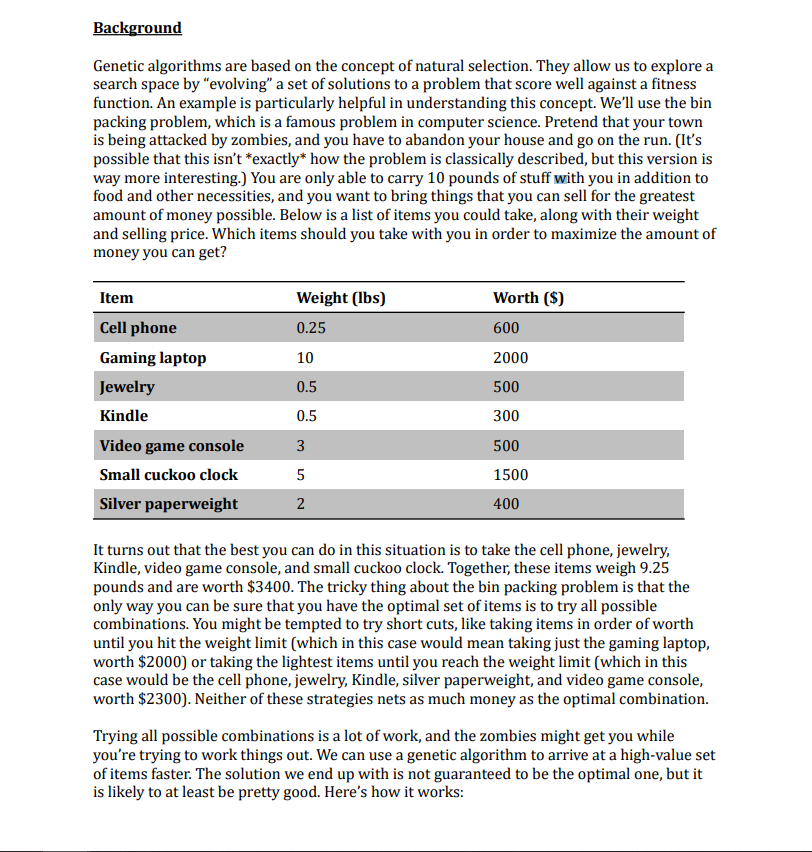
Background Genetic algorithms are based on the concept of natural selection. They allow us to explore a search space by "evolving" a set of solutions to a problem that score well against a fitness function. An example is particularly helpful in understanding this concept. We'll use the bin packing problem, which is a famous problem in computer science. Pretend that your town is being attacked by zombies, and you have to abandon your house and go on the run. (It's possible that this isn't *exactly* how the problem is classically described, but this version is way more interesting.) You are only able to carry 10 pounds of stuff with you in addition to food and other necessities, and you want to bring things that you can sell for the greatest amount of money possible. Below is a list of items you could take, along with their weight and selling price. Which items should you take with you in order to maximize the amount of money you can get? Worth ($) 600 Item Cell phone Gaming laptop Jewelry Kindle Video game console Small cuckoo clock Silver paperweight Weight (lbs) 0.25 10 0.5 0.5 2000 500 300 3 500 5 1500 2 400 It turns out that the best you can do in this situation is to take the cell phone, jewelry, Kindle, video game console, and small cuckoo clock. Together, these items weigh 9.25 pounds and are worth $3400. The tricky thing about the bin packing problem is that the only way you can be sure that you have the optimal set of items is to try all possible combinations. You might be tempted to try short cuts, like taking items in order of worth until you hit the weight limit (which in this case would mean taking just the gaming laptop, worth $2000) or taking the lightest items until you reach the weight limit (which in this case would be the cell phone, jewelry, Kindle, silver paperweight, and video game console, worth $2300). Neither of these strategies nets as much money as the optimal combination. Trying all possible combinations is a lot of work, and the zombies might get you while you're trying to work things out. We can use a genetic algorithm to arrive at a high-value set of items faster. The solution we end up with is not guaranteed to be the optimal one, but it is likely to at least be pretty good. Here's how it works: Problem Representation For our problem, we will represent an individual chromosome as a sequence of seven Item objects that correspond to the seven items we could possibly take with us. The Item class will contain fields for the type of item, its weight and value, and a boolean field called "included. False indicates we should leave that item behind, and true indicates we should take it with us. For example, if a chromosome has items with these included field values: TFFETTF it means we should take the cell phone, video game console, and small cuckoo clock (the first, fifth and sixth items in the table). Next, we need to develop some way to measure the "fitness" of each of our virtual organisms. In our problem, a set of items is better if it is worth more, provided that it weighs 10 pounds or less. We can therefore use the following as our fitness function: fitness(itemset) = 0 if weight(itemset) > 10; worth(itemset) otherwise where weight(itemset) equals the total weight of all of the items in the set and worth itemset) equals the total worth of all of the items in the set. Crossover and Mutation The two main operations in evolutionary computing are crossover and mutation. Crossover works like this: Randomly choose two parents from the population. Let's say these: Parent 1: TFTETTE Parent 2: TTTFETT Those two parents will create a child whose DNA is related to the parents? It works like this: for each of the seven genes in the chromosome, we will randomly pick a number between 1 and 10 and use it to choose which parents' value the child will get. If the random number is 1 through 5, we will use Parent l's included value for the child; if it is 6 through 10, we'll use Parent 2's. Let's assume our seven random numbers are: 1 4 10 3 6 6 9 Then the child's set of item included fields would be: Child: TFTFFIT Mutation is even simpler: we choose a single individual from our population and again generate a random number between 1 and 10 for each nucleotide. Mutation generally happens more rarely than reproduction, so if the random number is 1, we will flip that gene in the individual; otherwise, we will leave it the same. Let's assume our seven random numbers are: 5 1 7 8 9 2 7 and the chosen individual's included values are: TTFTTTF Then after mutation, that individual now looks like this (with the second gene flipped from a T to a F): TFFITTE Running the Genetic Algorithm Ok, now we have all of the pieces in place, and we can apply the genetic algorithm we've developed to our bin packing problem by following the steps below. 1. Create a set of ten random individuals to serve as the initial population 2. Add each of the individuals in the current population to the next generation 3. Randomly pair off the individuals and perform crossover to create a child and add it to the next generation as well. 4. Randomly choose ten percent of the individuals in the next generation and expose them to mutation 5. Sort the individuals in the next generation according to their fitness 6. Clear out the current population and add the top ten of the next generation back into the population 7. Repeat steps 2 through 6 twenty times 8. Sort the population and display the fittest individual to the console Implementation For this project, you will need to implement the following three classes. Your code must conform to this specification exactly (i.e. your classes and methods must be named as shown below and you must have the same method signatures). public class Item private final String name A label for the item, such as "Jewelry" or "Kindle" private final double weight The weight of the item in pounds private final int value The value of the item rounded to the nearest dollar private boolean included Indicates whether the item should be taken or not public Item(String name, double weight, int value) Initializes the Item's fields to the values that are passed in; the included field is initialized to false public Item(Item other) Initializes this item's fields to the be the same as the other item's public double getWeight() public int getValue() public boolean isIncluded() Getter for the item's fields (you don't need a getter for the name) public void setIncluded (boolean included) Setter for the item's included field (you don't need setters for the other fields) public String toString() Displays the item in the form ( lbs, $) public class Chromosome extends ArrayList implements Comparable private static Random rng Used for random number generation public Chromosome() This no-arg constructor can be empty public Chromosome (ArrayList items) Adds a copy of each of the items passed in to this Chromosome. Uses a random number to decide whether each item's included field is set to true or false. public Chromosome crossover (Chromosome other) Creates and returns a new child chromosome by performing the crossover operation on this chromosome and the other one that is passed in (i.e. for each item, use a random number to decide which parent's item should be copied and added to the child). public void mutate() Performs the mutation operation on this chromosome (i.e. for each item in this chromosome, use a random number to decide whether or not to flip it's included field from true to false or vice versa). public int getFitness() Returns the fitness of this chromosome. If the sum of all of the included items' weights are greater than 10, the fitness is zero. Otherwise, the fitness is equal to the sum of all of the included items' values. public int compareTo (Chromosome other) Returns -1 if this chromosome's fitness is greater than the other's fitness, +1 if this chromosome's fitness is less than the other one's, and 0 if their fitness is the same. public String toString() Displays the name, weight and value of all items in this chromosome whose included value is true, followed by the fitness of this chromosome. public class GeneticAlgorithm public static ArrayList readData(String filename) throws FileNotFoundException Reads in a data file with the format shown below and creates and returns an ArrayList of Item objects. item1_label, item1_weight, iteml_value item2_label, item2_weight, item2_value public static ArrayList initialize Population ArrayList items, int population Size) Creates and returns an ArrayList of population Size Chromosome objects that each contain the items, with their included field randomly set to true or false. public static void main(String[] args) throws FileNotFoundException Reads the data about the items in from a file called items.txt and performs the steps described in the Running the Genetic Algorithm section above. Background Genetic algorithms are based on the concept of natural selection. They allow us to explore a search space by "evolving" a set of solutions to a problem that score well against a fitness function. An example is particularly helpful in understanding this concept. We'll use the bin packing problem, which is a famous problem in computer science. Pretend that your town is being attacked by zombies, and you have to abandon your house and go on the run. (It's possible that this isn't *exactly* how the problem is classically described, but this version is way more interesting.) You are only able to carry 10 pounds of stuff with you in addition to food and other necessities, and you want to bring things that you can sell for the greatest amount of money possible. Below is a list of items you could take, along with their weight and selling price. Which items should you take with you in order to maximize the amount of money you can get? Worth ($) 600 Item Cell phone Gaming laptop Jewelry Kindle Video game console Small cuckoo clock Silver paperweight Weight (lbs) 0.25 10 0.5 0.5 2000 500 300 3 500 5 1500 2 400 It turns out that the best you can do in this situation is to take the cell phone, jewelry, Kindle, video game console, and small cuckoo clock. Together, these items weigh 9.25 pounds and are worth $3400. The tricky thing about the bin packing problem is that the only way you can be sure that you have the optimal set of items is to try all possible combinations. You might be tempted to try short cuts, like taking items in order of worth until you hit the weight limit (which in this case would mean taking just the gaming laptop, worth $2000) or taking the lightest items until you reach the weight limit (which in this case would be the cell phone, jewelry, Kindle, silver paperweight, and video game console, worth $2300). Neither of these strategies nets as much money as the optimal combination. Trying all possible combinations is a lot of work, and the zombies might get you while you're trying to work things out. We can use a genetic algorithm to arrive at a high-value set of items faster. The solution we end up with is not guaranteed to be the optimal one, but it is likely to at least be pretty good. Here's how it works: Problem Representation For our problem, we will represent an individual chromosome as a sequence of seven Item objects that correspond to the seven items we could possibly take with us. The Item class will contain fields for the type of item, its weight and value, and a boolean field called "included. False indicates we should leave that item behind, and true indicates we should take it with us. For example, if a chromosome has items with these included field values: TFFETTF it means we should take the cell phone, video game console, and small cuckoo clock (the first, fifth and sixth items in the table). Next, we need to develop some way to measure the "fitness" of each of our virtual organisms. In our problem, a set of items is better if it is worth more, provided that it weighs 10 pounds or less. We can therefore use the following as our fitness function: fitness(itemset) = 0 if weight(itemset) > 10; worth(itemset) otherwise where weight(itemset) equals the total weight of all of the items in the set and worth itemset) equals the total worth of all of the items in the set. Crossover and Mutation The two main operations in evolutionary computing are crossover and mutation. Crossover works like this: Randomly choose two parents from the population. Let's say these: Parent 1: TFTETTE Parent 2: TTTFETT Those two parents will create a child whose DNA is related to the parents? It works like this: for each of the seven genes in the chromosome, we will randomly pick a number between 1 and 10 and use it to choose which parents' value the child will get. If the random number is 1 through 5, we will use Parent l's included value for the child; if it is 6 through 10, we'll use Parent 2's. Let's assume our seven random numbers are: 1 4 10 3 6 6 9 Then the child's set of item included fields would be: Child: TFTFFIT Mutation is even simpler: we choose a single individual from our population and again generate a random number between 1 and 10 for each nucleotide. Mutation generally happens more rarely than reproduction, so if the random number is 1, we will flip that gene in the individual; otherwise, we will leave it the same. Let's assume our seven random numbers are: 5 1 7 8 9 2 7 and the chosen individual's included values are: TTFTTTF Then after mutation, that individual now looks like this (with the second gene flipped from a T to a F): TFFITTE Running the Genetic Algorithm Ok, now we have all of the pieces in place, and we can apply the genetic algorithm we've developed to our bin packing problem by following the steps below. 1. Create a set of ten random individuals to serve as the initial population 2. Add each of the individuals in the current population to the next generation 3. Randomly pair off the individuals and perform crossover to create a child and add it to the next generation as well. 4. Randomly choose ten percent of the individuals in the next generation and expose them to mutation 5. Sort the individuals in the next generation according to their fitness 6. Clear out the current population and add the top ten of the next generation back into the population 7. Repeat steps 2 through 6 twenty times 8. Sort the population and display the fittest individual to the console Implementation For this project, you will need to implement the following three classes. Your code must conform to this specification exactly (i.e. your classes and methods must be named as shown below and you must have the same method signatures). public class Item private final String name A label for the item, such as "Jewelry" or "Kindle" private final double weight The weight of the item in pounds private final int value The value of the item rounded to the nearest dollar private boolean included Indicates whether the item should be taken or not public Item(String name, double weight, int value) Initializes the Item's fields to the values that are passed in; the included field is initialized to false public Item(Item other) Initializes this item's fields to the be the same as the other item's public double getWeight() public int getValue() public boolean isIncluded() Getter for the item's fields (you don't need a getter for the name) public void setIncluded (boolean included) Setter for the item's included field (you don't need setters for the other fields) public String toString() Displays the item in the form ( lbs, $) public class Chromosome extends ArrayList implements Comparable private static Random rng Used for random number generation public Chromosome() This no-arg constructor can be empty public Chromosome (ArrayList items) Adds a copy of each of the items passed in to this Chromosome. Uses a random number to decide whether each item's included field is set to true or false. public Chromosome crossover (Chromosome other) Creates and returns a new child chromosome by performing the crossover operation on this chromosome and the other one that is passed in (i.e. for each item, use a random number to decide which parent's item should be copied and added to the child). public void mutate() Performs the mutation operation on this chromosome (i.e. for each item in this chromosome, use a random number to decide whether or not to flip it's included field from true to false or vice versa). public int getFitness() Returns the fitness of this chromosome. If the sum of all of the included items' weights are greater than 10, the fitness is zero. Otherwise, the fitness is equal to the sum of all of the included items' values. public int compareTo (Chromosome other) Returns -1 if this chromosome's fitness is greater than the other's fitness, +1 if this chromosome's fitness is less than the other one's, and 0 if their fitness is the same. public String toString() Displays the name, weight and value of all items in this chromosome whose included value is true, followed by the fitness of this chromosome. public class GeneticAlgorithm public static ArrayList readData(String filename) throws FileNotFoundException Reads in a data file with the format shown below and creates and returns an ArrayList of Item objects. item1_label, item1_weight, iteml_value item2_label, item2_weight, item2_value public static ArrayList initialize Population ArrayList items, int population Size) Creates and returns an ArrayList of population Size Chromosome objects that each contain the items, with their included field randomly set to true or false. public static void main(String[] args) throws FileNotFoundException Reads the data about the items in from a file called items.txt and performs the steps described in the Running the Genetic Algorithm section above