Based on the information in the attached images, answer this tenth question.

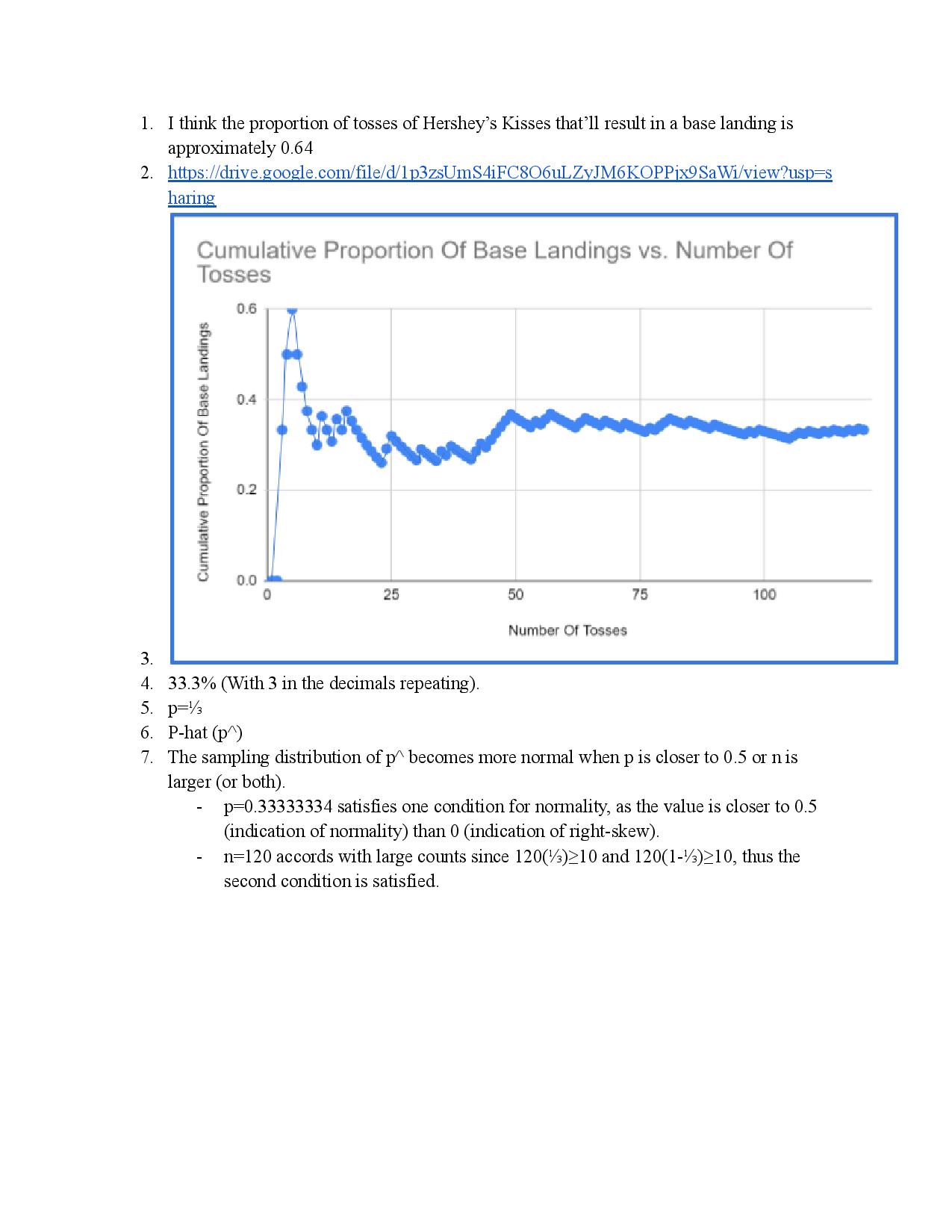
10. There is no way to know whether the confidence interval you constructed actually "catches" the true proportion p of times that your Hershey's Kiss will land on its base. What we can say is that the method you used will succeed in capturing the unknown population parameter about 95% of the time. Likewise, we expect that about 95% of all the confidence intervals drawn by the members of your class will capture p. Would it be unusual to find out that one of your classmates' confidence intervals did not contain the true proportion p? Explain with words and a numerical calculation.

1. I think the proportion of tosses of Hershey's Kisses that'll result in a base landing is approximately 0.64 2. https://drive.google.com/file/d/1p3zsUmS4iFC806ulZyJM6KOPPjx9 SaWi/view?usp=s haring Cumulative Proportion Of Base Landings vs. Number Of Tosses 0.6 0.4 Cumulative Proportion Of Base Landings 0.2 0.0 25 50 75 100 Number Of Tosses W 4. 33.3% (With 3 in the decimals repeating). 5. p=1/3 6. P-hat (p) 7. The sampling distribution of p becomes more normal when p is closer to 0.5 or n is larger (or both) p=0.33333334 satisfies one condition for normality, as the value is closer to 0.5 (indication of normality) than 0 (indication of right-skew) n=120 accords with large counts since 120(1/3)210 and 120(1-1/3)210, thus the second condition is satisfied8. Since n=120 satisfies the 10% condition [120