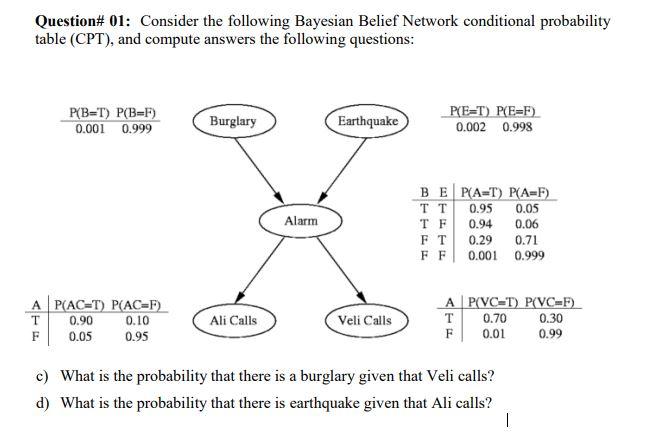
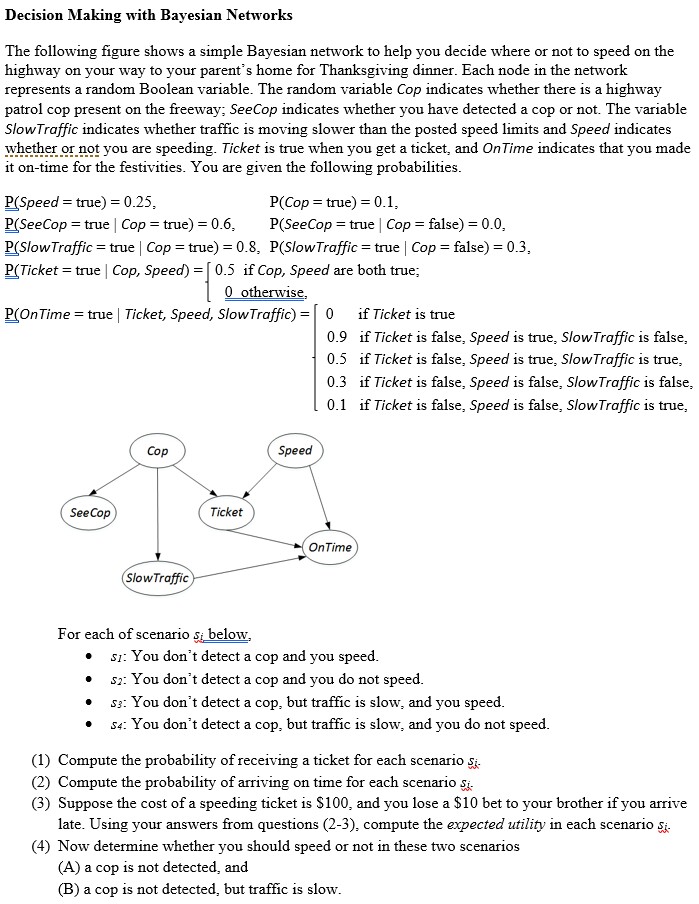
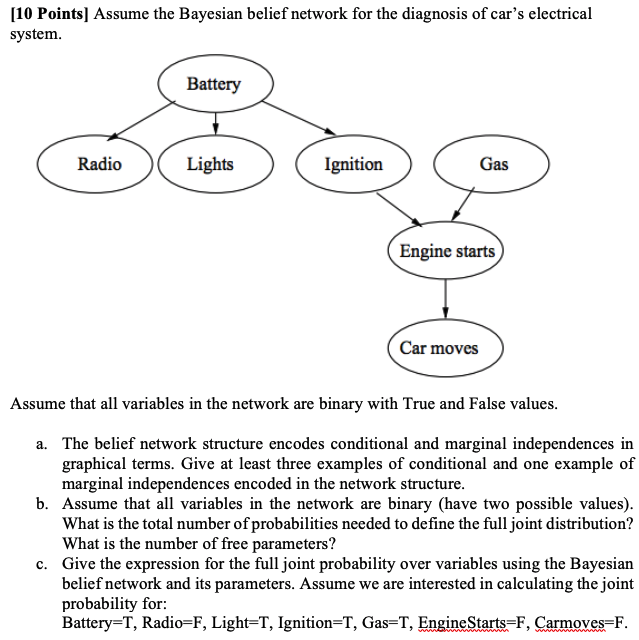
Bayesian Networks, Netica (12+14+22+3+1x 10+ 7 = 40 marks) Expand the Bayes Net you developed in the BN tutorial (available on moodle under the name SmokeAlarm.dne) to include three more events: Smoke (you can see smoke in your apartment), Evacu- ation (your apartment building is evacuated), and Report (the local newspaper writes a report about the evacuation of your apartment). The probability of smoke when there is fire is 0.95, the probability of smoke when there is no fire is 0.05. When your apartment building has a fire alarm, there is a 0.9 probability that there will be an evacuation, but there is never an evacuation when there is no fire alarm. If there is an evacuation, there is a 0.7 probability that the newspaper will write a report on it, and if there is no evacuation there is a 0.9 probability that the newspaper won't report it. (a) Add the necessary nodes and edges to your BN, and input the corresponding conditional prob- ability tables. Justify your expanded network and CPTS. A BN without justification will receive no marks. (b) Use Netica on the expanded BN to answer the following questions: i. What is the marginal probability that your smoke detector has been tampered with? ii. What is the marginal probability that there will be a news report tomorrow? iii. Let's assume that you have observed that there is smoke in your apartment. What is the posterior probability that there will be a news report tomorrow? iv. Let's assume that you have observed that there was no fire, and that there was a news report about your apartment. What is the posterior probability that your smoke detector has been tampered with? v. Let's assume that you have observed that there is no smoke in your apartment. What is the posterior probability that your smoke detector has been tampered with? What conditional independence property could help you here? vi. Let's assume that you have observed that there has been a news report about your apart- ment, and there is no smoke in your apartment. What is the posterior probability that your smoke detector has been tampered with? Given that the news report was observed, why does observing the absence of smoke affect your belief of whether or not your smoke alarm was tampered with? vii. Let's assume that you have observed that there was no fire, that there was a news report about your apartment, and that there is smoke in your apartment. What is the posterior probability that your smoke detector has been tampered with? How does observing whether or not there is smoke affect your belief of whether or not your smoke detector has been tampered with? Why? 5. Bayesian Belief Network Consider the following Bayesian network consisting of five Boolean random variables A, B, C, D, E. A D B E a) Given the above Bayesian network derive a formula each to compute the probability of: (1) A and E are true, and B, C, D are false; (2) D given information about A and E. b) Assume that in addition to being given the above Bayesian network, you are also told that: (1) P(E|B,C,D) = P(EID) (2) P(D|A,B,C) = P(D|B,C) (3) P(C|A,B) = P(CIA) What changes does this additional information allow you to make to the above Bayesian network? Explain why you can make these changes and draw the resulting Bayesian network. 5. Bayesian Belief Network Consider the following Bayesian network consisting of five Boolean random variables A, B, C, D, E. A D B E a) Given the above Bayesian network derive a formula each to compute the probability of: (1) A and E are true, and B, C, D are false; (2) D given information about A and E. b) Assume that in addition to being given the above Bayesian network, you are also told that: (1) P(E|B,C,D) = P(EID) (2) P(D|A,B,C) = P(D|B,C) (3) P(C|A,B) = P(CIA) What changes does this additional information allow you to make to the above Bayesian network? Explain why you can make these changes and draw the resulting Bayesian network. Question# 01: Consider the following Bayesian Belief Network conditional probability table (CPT), and compute answers the following questions: P(B-T) P(B-F) 0.001 0.999 A P(AC-T) P(AC-F) T 0.90 0.10 F 0.05 0.95 Burglary Ali Calls Alarm Earthquake Veli Calls P(E=T) P(E=F) 0.002 0.998 BE|P(A=T) P(A=F) TT 0.95 0.05 TF 0.94 0.06 FT 0.29 0.71 FF 0.001 0.999 A| P(VC=T) P(VC=F) T 0.70 0.30 F 0.01 0.99 c) What is the probability that there is a burglary given that Veli calls? d) What is the probability that there is earthquake given that Ali calls? I Bayesian Belief Networks: An Example CPT: Conditional Probability Table Bayesian Belief Network Sprinkler Grass wet PRILO FANT F F 044 TON W Rain STAGI SPRINKLER MAIN T F F T 0.01 0.99 COMISIE F Derivation of the probability of a particular n combination of values of X, from CPT: P(x,...,x) = II P(xi Parents (Y;)) i=1 Bayesian Belief Networks: An Example Pr(R-T|G-T) = SPRINT SPRINKLER RANT F F 0.4 0.6 T 0.00 0.99 SMINKLER MAT I 23 10 02 23 01 GRASSWET F T T BAN GRASS WET SPRINKLER FANT F SPRINKLER F 0.0 1.0 T The joint probability function: Pr(G, S, R) = Pr(G | S, R) Pr(S | R) Pr(R) The model can answer the question like: what is the probability that it is raining, given the grass is wet? The corresponding conditional probability function: GMASSWET 0.8 0.2 T 0.59 0.00 shows the conditional probability for each possible combination of its parents F 0.9 T 0.99 0.01 GRASS WET SPRINKLER KAN T F F T Pr(G=T, R=T) Esrr Pr(G-T, S.R=T') Pr(GT) s,Rr.F) Pr(G=T, S, R) Bayesian Belief Networks: An Example PAIN 1.0 F0.0 T 0.8 0.2 MAIN T F 0.2 48 MAIN T F 0.2 08 Let's calculate the conditional probability: Pr(R=T|G=T) = Pr(G-T,R=T) Estr. Pr(G=T, S, R=T) ERIT,F) Pr(G-T, S, R) Pr(G-T) Next we need to calculate: Pr(G= T) which is a sum of 4 probabilities 0.0019877 0.15847 891 Finally: Pr(RT | G=T) = 0.00198TTT +0.288TTF +0.1584TFT +0.0TFF 2491 Pr(GT, ST, R = T) = Pr(G=T|S=T,R=T) Pr(S = T | R = T) Pr(R = T) = 0.99 0.01 x 0.2 = 0.00198. Now we need to do this: Pr(G = T, S = F, R= T) 35.77%. 2. Suppose each random variable takes three states, i.e., A can take values in {ao, ai, a2), B can take values in {bo, b,b2} and so on. What is the minimum number of parameters to exactly express the above model, i.e., to express the joint distributions p(A, B, C, D, E, F) (2.5 marks)? Please also justify your answer (2.5 marks). (In total 5 marks) 3. Check whether the following statements are true. If you think the statements are true, then type T, otherwise type F. Please just type five characters for the five questions in order. For example, if you think the first four are true and the last is false, then simply type TTTTF. We also need you to justify your answer in the last bullet. A and B are independent (0.5 mark) -A and B are conditionally independent given D (0.5 mark) A and E are conditionally independent given D (0.5 mark) - E and F are independent (0.5 mark) -E and F are conditionally independent given D (0.5 mark). Use the expression of joint distribution to justify your answer, i.e., either prove the independency or show it does not hold (2.5 marks). Hint: there is no need to consider all random variables in the Bayesian network. 4. Suppose each random variable only takes two states, i.e., A can take values in {ao, a1}, B can take values in {bo, bi} and so on. Suppose the (conditional) probability tables of this model are as follows. Decision Making with Bayesian Networks The following figure shows a simple Bayesian network to help you decide where or not to speed on the highway on your way to your parent's home for Thanksgiving dinner. Each node in the network represents a random Boolean variable. The random variable Cop indicates whether there is a highway patrol cop present on the freeway; SeeCop indicates whether you have detected a cop or not. The variable Slow Traffic indicates whether traffic is moving slower than the posted speed limits and Speed indicates whether or not you are speeding. Ticket is true when you get a ticket, and On Time indicates that you made it on-time for the festivities. You are given the following probabilities. P(Speed = true) = 0.25, P(Cop=true) = 0.1, P(SeeCop = true | Cop = true) = 0.6, P(SeeCop=true | Cop= false) = 0.0 P(Slow Traffic = true | Cop=true) = 0.8, P(SlowTraffic = true | Cop = false) = 0.3, P(Ticket = true | Cop, Speed) = [0.5 if Cop, Speed are both true; 0 otherwise, = true | Ticket, Speed, Slow Traffic) = 0 P(On Time: See Cop Cop . (Slow Traffic Ticket For each of scenario si below. Speed if Ticket is true 0.9 if Ticket is false, Speed is true, Slow Traffic is false, 0.5 if Ticket is false, Speed is true, Slow Traffic is true, 0.3 if Ticket is false, Speed is false, Slow Traffic is false, 0.1 if Ticket is false, Speed is false, Slow Traffic is true, OnTime S1: You don't detect a cop and you speed. 52: You don't detect a cop and you do not speed. 53: You don't detect a cop, but traffic is slow, and you speed. 54: You don't detect a cop, but traffic is slow, and you do not speed. (1) Compute the probability of receiving a ticket for each scenario i. (2) Compute the probability of arriving on time for each scenario Si. (3) Suppose the cost of a speeding ticket is $100, and you lose a $10 bet to your brother if you arrive late. Using your answers from questions (2-3), compute the expected utility in each scenario si- (4) Now determine whether you should speed or not in these two scenarios (A) a cop is not detected, and (B) a cop is not detected, but traffic is slow. [10 Points] Assume the Bayesian belief network for the diagnosis of car's electrical system. Radio Battery Lights Ignition Gas Engine starts Car moves Assume that all variables in the network are binary with True and False values. a. The belief network structure encodes conditional and marginal independences in graphical terms. Give at least three examples of conditional and one example of marginal independences encoded in the network structure. b. Assume that all variables in the network are binary (have two possible values). What is the total number of probabilities needed to define the full joint distribution? What is the number of free parameters? c. Give the expression for the full joint probability over variables using the Bayesian belief network and its parameters. Assume we are interested in calculating the joint probability for: Battery=T, Radio=F, Light-T, Ignition=T, Gas-T, EngineStarts-F, Carmoves=F.