Question: Below are the questions: Below are the Header and Class file for problem number 2 1. (10 points) The price of an item that you
Below are the questions:


Below are the Header and Class file for problem number 2
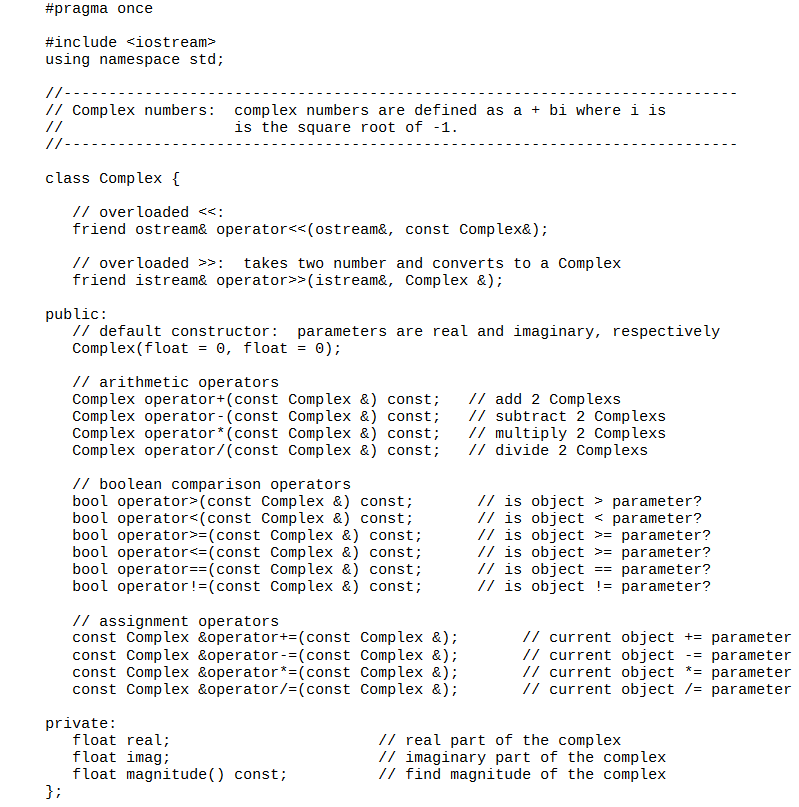



1. (10 points) The price of an item that you want to buy is given by two integers as priceDollars dollars and priceCents cents. You pay for it in cash by giving the clerk payDollars dollars and payCents cents. Write specifications (documentation) for a method that computes the change, if any, that you should receive. The correct change should be passed back in two method parameters as changeDollars and changeCents (that are passed by reference). Include a statement of purpose, the pre-and postconditions, and a description of the parameters. Be precise in the relationship between the inputs and outputs (don't just say, the correct change is computed"). Do not write code to implement the function. Just write the specifications. Do not using floating point; money is not subject to round-off error. 2. (10 points) Write a method to implement operator for the Complex class from Lecture 3. This method should result in the number having one added to the real component and return the new value of the number. This is the prefix version of the operator, so it would be used like this: Complex b = a; Write the code that would be in the cpp file. The header file contains: Complex &operator+ 0); // increments a Complex number by one FYI: The postfix version is similar, but uses a dummy int parameter to distinguish itself from the prefix version. The postfix version also returns by value, instead of reference. 3. (12 points) Consider an abstract data type (ADT) for polynomials (in a single variable x) whose operations include the following: int degree // Returns the degree of the polynomial. int coefficient(int power) // Returns the coefficient of the power term. void changeCoefficient(int newCoefficient, int power) I/Replaces the coefficient of the power term with newCoefficient For this problem, consider only polynomials whose exponents are nonnegative integers. For example, p = 4x5 +7x3-X2 +9 The following examples demonstrate the ADT operations on the above polynomial. p.degree) is 5 (the highest power of a term with a nonzero coefficient) p.coefficient(3) is 7 (note that the coefficient of a missing term is implicitly 0) p.changeCoefficient(-3,7) produces the polynomial p=-3x7 + 4x + 7x3 - x2 + 9 Using these ADT operations, write C++ statements to perform the following tasks for an arbitrary polynomial q. 1. Display the coefficient of the term that has the highest power to the console output. 2. Decrease the coefficient of the x2 term by 3. 3. Compute the sum of two polynomials q and r. Place the result in a third polynomials that has been previously initialized to zero. 4.(12 points) Write a template function that takes as a parameter a vector of objects of some unknown class and two objects obj1 and obj2 of the same class. Modify the input vector to replace every instance of obji in the vector with obj2. If no instances of obj1 are found, add a new element at the end of the vector containing obj2. The function is not a member of any class (Recall that you can access vectors like arrays, but they have useful methods like sies and push_baek Vector declarations look like this: vectorcsontype varians Vectors are also covered further in the book in Section A8 - page 737) 5. (10 points) Write a recursive method that returns the number of 1s in the binary representation of n (an integer parameter to your method). Use the fact that the number of ones in nequals the number of 1s in the binary representation of /2, plus 1.in is odd. (Note that you don't add 1 ton/2 You add one to the number of 1s in the binary representation of 1/2) The answer for 25 would be 3, since the binary representation is 11001 For negative numbers, return the number of ones in the absolute value 6. (16 points) This problem considers several ways to computex" for integers x and n20. a Write an iterative function power to computex" for n 20. b. Write a recursive function power to computexe" by using the following recursive formulation x=1 =x*x+1 ifn> 0 c. Write a recursive function power to computex" by using the following recursive formulation x = 1 X = (/22 ifn >0 and n is even x=x*(x-1122 ifn >O and n is odd Make only one recursive call each time through the function, so that it operates efficiently. d. What is the running time of each of the above algorithms as function of n? Use Big-O notation and justify your answer. 7.(12 points) Prove using induction: na + 2n is divisible by 3 for alln>0. 8. (12 points) Let Fin) be the Fibonacci sequence. Prove using induction F(i) - F(n+2) - 1 for alln>0. (The sum of the first n Fibonacci numbers is equal to Fin+2) - 1 Use F(1)= F2) = 1) 9.(6 points) Which of the following functions are in? (Remember that Big-O notation provides an upper bound only) a. na/10 b. 15n-1 c6n2 +12n+8 d. n logn - 10 en/tin-2-in-3)) t2n #pragma once #include using namespace std; // ----- - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // Complex numbers: complex numbers are defined as a + bi where is the square root of -1. //--------- class Complex { // over loaded >: takes two number and converts to a Complex friend istream& operator>>(istream&, Complex &); public: // default constructor: parameters are real and imaginary, respectively Complex(float = 0, float = 0); // arithmetic operators Complex operator+(const Complex & const; Complex operator-(const Complex & const; Complex operator*(const Complex & const; Complex operator/(const Complex & const; // add 2 Complexs // subtract 2 Complexs // multiply 2 Complexs // divide 2 Complexs // boolean comparison operators bool operator>(const Complex & const; bool operator=(const Complex & const; bool operator parameter? // is object = parameter? // is object >= parameter? // is object == parameter? // is object != parameter? // assignment operators const Complex &operator+=(const Complex &); const Complex &operator-=(const Complex &); const Complex &operator*=(const Complex &); const Complex &operator/=(const Complex &); // current object += parameter Il current object -= parameter // current object *= parameter // current object /= parameter private: float real; float imag; float magnitude // real part of the complex // imaginary part of the complex // find magnitude of the complex const; #include #include "Complex.h" 1 .- ---------- Complex ---------- // default constructor: parameters are numerator and denominator respectively Complex:: Complex(float r, float i) { real = r; imag = i; //----- ------- -- + --------------------- // over loaded +: addition of 2 Complexs, current object and parameter Complex Complex:: operator+(const Complex& a) const { Complex sum; sum. real = a.real + real; sum. imag = a.imag + imag; return sum; // -- // over Loaded - subtraction of 2 Complexs, current object and parameter Complex Complex:: operator-(const complex& s) const { Complex sub; sub.real = real - s.real; sub.imag = imag - s.imag; return sub; // // overloaded *: multiplication of 2 Complexs, current object and parameter Complex Comp lex:: operator*(const Complex& m) const { Complex mult; mult.real = m.real i real - m.imag * imag; mult.imag = m. real timag + real * m.imag; return mult; //-- ------------- ------ // over loaded /: division of 2 Complexs, current object and parameter, division by zero terminates prog Complex Complex:: operator/(const Complex& v) const { Complex div; if (v.real != || v. imag != 0) { // make sure new denominator != zero float denom = v.real i v.real + v.imag * v.imag; div.real = (real * v.real + imag * v.imag) / denom; div.imag = (imag * v.real - real * v.imag) / denom; else { cout : true if current object magnitude is > parameter, otherwise false bool Complex:: operator>(const complex& r) const { return magnitude(> r.magnitude(); - - - - - - - - - - - - - - - - - - - - // -- ---- // over loaded <: true if current object is parameter otherwise false bool complex: operator complex r const return magnitude .................------------------>= ----------- // over loaded : true if current object is >= parameter, otherwise false bool Complex:: operator>=(const complex& r) const { return!(*this r); // ------------ ------------------ == ----------------------- // over Loaded == true if current object is == parameter, otherwise false bool Complex:: operator==(const complex& r) const { return (real == r.real && imag == r. imag); // --- --- --------- - --- ------------- // over loaded != true if current object is != parameter, otherwise false bool Complex::operator !=(const complex& r) const { return!(*this == n); // over loaded +=: current object = current object + parameter const Complex& Complex:: operator+=(const complex& a) { *this = *this + a; return *this; // ----------- // over Loaded -=: current object = current object - parameter const complex& Complex::operator -=(const complex& a) { *this = *this - a; return this; //------------- // over loaded :=: current object = current object * parameter const complex& Complex:: operatort=(const complex& a) { *this = *this * a; return this; //--- ------------ = ---------------- // over Loaded /= current object = current object / parameter const complex& Complex::operator/=(const complex& a) { *this = *this / a; return "this; // ------ - // over Loaded = 0) output r.real > ---------------------- // over loaded >>: takes 2 ints as numerator and denominator, does no 11 error checking, standard c casting between floats, char, etc occurs istream& operator>>(istream &input, Complex &r) { input >> r.real >> r.imag; return input; // -------------------------------- magnitude ---------------------------- // compute magnitude of float and cast it into template float type float Complex::magnitude() const { return float(sqrt(real real + imag imag)); 1. (10 points) The price of an item that you want to buy is given by two integers as priceDollars dollars and priceCents cents. You pay for it in cash by giving the clerk payDollars dollars and payCents cents. Write specifications (documentation) for a method that computes the change, if any, that you should receive. The correct change should be passed back in two method parameters as changeDollars and changeCents (that are passed by reference). Include a statement of purpose, the pre-and postconditions, and a description of the parameters. Be precise in the relationship between the inputs and outputs (don't just say, the correct change is computed"). Do not write code to implement the function. Just write the specifications. Do not using floating point; money is not subject to round-off error. 2. (10 points) Write a method to implement operator for the Complex class from Lecture 3. This method should result in the number having one added to the real component and return the new value of the number. This is the prefix version of the operator, so it would be used like this: Complex b = a; Write the code that would be in the cpp file. The header file contains: Complex &operator+ 0); // increments a Complex number by one FYI: The postfix version is similar, but uses a dummy int parameter to distinguish itself from the prefix version. The postfix version also returns by value, instead of reference. 3. (12 points) Consider an abstract data type (ADT) for polynomials (in a single variable x) whose operations include the following: int degree // Returns the degree of the polynomial. int coefficient(int power) // Returns the coefficient of the power term. void changeCoefficient(int newCoefficient, int power) I/Replaces the coefficient of the power term with newCoefficient For this problem, consider only polynomials whose exponents are nonnegative integers. For example, p = 4x5 +7x3-X2 +9 The following examples demonstrate the ADT operations on the above polynomial. p.degree) is 5 (the highest power of a term with a nonzero coefficient) p.coefficient(3) is 7 (note that the coefficient of a missing term is implicitly 0) p.changeCoefficient(-3,7) produces the polynomial p=-3x7 + 4x + 7x3 - x2 + 9 Using these ADT operations, write C++ statements to perform the following tasks for an arbitrary polynomial q. 1. Display the coefficient of the term that has the highest power to the console output. 2. Decrease the coefficient of the x2 term by 3. 3. Compute the sum of two polynomials q and r. Place the result in a third polynomials that has been previously initialized to zero. 4.(12 points) Write a template function that takes as a parameter a vector of objects of some unknown class and two objects obj1 and obj2 of the same class. Modify the input vector to replace every instance of obji in the vector with obj2. If no instances of obj1 are found, add a new element at the end of the vector containing obj2. The function is not a member of any class (Recall that you can access vectors like arrays, but they have useful methods like sies and push_baek Vector declarations look like this: vectorcsontype varians Vectors are also covered further in the book in Section A8 - page 737) 5. (10 points) Write a recursive method that returns the number of 1s in the binary representation of n (an integer parameter to your method). Use the fact that the number of ones in nequals the number of 1s in the binary representation of /2, plus 1.in is odd. (Note that you don't add 1 ton/2 You add one to the number of 1s in the binary representation of 1/2) The answer for 25 would be 3, since the binary representation is 11001 For negative numbers, return the number of ones in the absolute value 6. (16 points) This problem considers several ways to computex" for integers x and n20. a Write an iterative function power to computex" for n 20. b. Write a recursive function power to computexe" by using the following recursive formulation x=1 =x*x+1 ifn> 0 c. Write a recursive function power to computex" by using the following recursive formulation x = 1 X = (/22 ifn >0 and n is even x=x*(x-1122 ifn >O and n is odd Make only one recursive call each time through the function, so that it operates efficiently. d. What is the running time of each of the above algorithms as function of n? Use Big-O notation and justify your answer. 7.(12 points) Prove using induction: na + 2n is divisible by 3 for alln>0. 8. (12 points) Let Fin) be the Fibonacci sequence. Prove using induction F(i) - F(n+2) - 1 for alln>0. (The sum of the first n Fibonacci numbers is equal to Fin+2) - 1 Use F(1)= F2) = 1) 9.(6 points) Which of the following functions are in? (Remember that Big-O notation provides an upper bound only) a. na/10 b. 15n-1 c6n2 +12n+8 d. n logn - 10 en/tin-2-in-3)) t2n #pragma once #include using namespace std; // ----- - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // Complex numbers: complex numbers are defined as a + bi where is the square root of -1. //--------- class Complex { // over loaded >: takes two number and converts to a Complex friend istream& operator>>(istream&, Complex &); public: // default constructor: parameters are real and imaginary, respectively Complex(float = 0, float = 0); // arithmetic operators Complex operator+(const Complex & const; Complex operator-(const Complex & const; Complex operator*(const Complex & const; Complex operator/(const Complex & const; // add 2 Complexs // subtract 2 Complexs // multiply 2 Complexs // divide 2 Complexs // boolean comparison operators bool operator>(const Complex & const; bool operator=(const Complex & const; bool operator parameter? // is object = parameter? // is object >= parameter? // is object == parameter? // is object != parameter? // assignment operators const Complex &operator+=(const Complex &); const Complex &operator-=(const Complex &); const Complex &operator*=(const Complex &); const Complex &operator/=(const Complex &); // current object += parameter Il current object -= parameter // current object *= parameter // current object /= parameter private: float real; float imag; float magnitude // real part of the complex // imaginary part of the complex // find magnitude of the complex const; #include #include "Complex.h" 1 .- ---------- Complex ---------- // default constructor: parameters are numerator and denominator respectively Complex:: Complex(float r, float i) { real = r; imag = i; //----- ------- -- + --------------------- // over loaded +: addition of 2 Complexs, current object and parameter Complex Complex:: operator+(const Complex& a) const { Complex sum; sum. real = a.real + real; sum. imag = a.imag + imag; return sum; // -- // over Loaded - subtraction of 2 Complexs, current object and parameter Complex Complex:: operator-(const complex& s) const { Complex sub; sub.real = real - s.real; sub.imag = imag - s.imag; return sub; // // overloaded *: multiplication of 2 Complexs, current object and parameter Complex Comp lex:: operator*(const Complex& m) const { Complex mult; mult.real = m.real i real - m.imag * imag; mult.imag = m. real timag + real * m.imag; return mult; //-- ------------- ------ // over loaded /: division of 2 Complexs, current object and parameter, division by zero terminates prog Complex Complex:: operator/(const Complex& v) const { Complex div; if (v.real != || v. imag != 0) { // make sure new denominator != zero float denom = v.real i v.real + v.imag * v.imag; div.real = (real * v.real + imag * v.imag) / denom; div.imag = (imag * v.real - real * v.imag) / denom; else { cout : true if current object magnitude is > parameter, otherwise false bool Complex:: operator>(const complex& r) const { return magnitude(> r.magnitude(); - - - - - - - - - - - - - - - - - - - - // -- ---- // over loaded <: true if current object is parameter otherwise false bool complex: operator complex r const return magnitude .................------------------>= ----------- // over loaded : true if current object is >= parameter, otherwise false bool Complex:: operator>=(const complex& r) const { return!(*this r); // ------------ ------------------ == ----------------------- // over Loaded == true if current object is == parameter, otherwise false bool Complex:: operator==(const complex& r) const { return (real == r.real && imag == r. imag); // --- --- --------- - --- ------------- // over loaded != true if current object is != parameter, otherwise false bool Complex::operator !=(const complex& r) const { return!(*this == n); // over loaded +=: current object = current object + parameter const Complex& Complex:: operator+=(const complex& a) { *this = *this + a; return *this; // ----------- // over Loaded -=: current object = current object - parameter const complex& Complex::operator -=(const complex& a) { *this = *this - a; return this; //------------- // over loaded :=: current object = current object * parameter const complex& Complex:: operatort=(const complex& a) { *this = *this * a; return this; //--- ------------ = ---------------- // over Loaded /= current object = current object / parameter const complex& Complex::operator/=(const complex& a) { *this = *this / a; return "this; // ------ - // over Loaded = 0) output r.real > ---------------------- // over loaded >>: takes 2 ints as numerator and denominator, does no 11 error checking, standard c casting between floats, char, etc occurs istream& operator>>(istream &input, Complex &r) { input >> r.real >> r.imag; return input; // -------------------------------- magnitude ---------------------------- // compute magnitude of float and cast it into template float type float Complex::magnitude() const { return float(sqrt(real real + imag imag))









