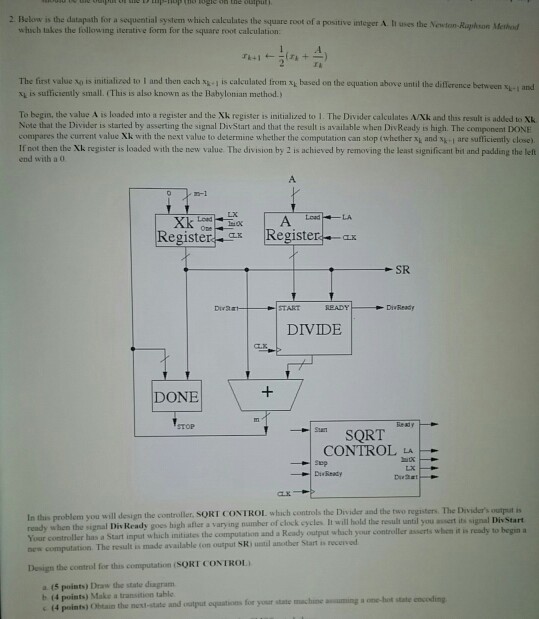
Below is the datapath for a sequential system which calculates the squareroot of a positive integer A h uses the Newton-Radisson Method which takes the following iterative form for the squareroot calculation: The first value x_0 is initialized to l and then each x_k-1 is calculated from X_k based on the equation above until the difference between X_L-1. and X_L is sufficiently small. (This is also known as the Babylonian method.) To begin, the value A is loaded into a register and the Xk register is initialized to 1 The Divider calculates A/Xk and this result is added to Xk Note that the Divider is started by asserting the signal Distort and that the result is available when DivReady is high. The component DONE compares the current value X_k with the next value to determine whether the computation can stop (whether X_k and X_k-1 are sufficiently close). If not, then the Xk register is loaded with the new value The division by 2 is achieved by removing the least significant bit and padding the left Register ax DIVIDE DONE Ready SORT CONTROL LA In this problem you will design the controller, SORT which controls the Divider and the two registers. The Dividers output is signal DiviReady goes high after a varying number of clock cycles It will hold the result until you assert its signal Distort controller asserts when Tool began ready when the and a Ready output your controller has a which the computation received new computation. The result is made available on output ski until another is Design the control for this computation (SORT CONTROL) a. Draw the state diagram b Make a table equations for your the Brachiated assuming a one-hot state encoding c. obtain the next-state and output Below is the datapath for a sequential system which calculates the squareroot of a positive integer A h uses the Newton-Radisson Method which takes the following iterative form for the squareroot calculation: The first value x_0 is initialized to l and then each x_k-1 is calculated from X_k based on the equation above until the difference between X_L-1. and X_L is sufficiently small. (This is also known as the Babylonian method.) To begin, the value A is loaded into a register and the Xk register is initialized to 1 The Divider calculates A/Xk and this result is added to Xk Note that the Divider is started by asserting the signal Distort and that the result is available when DivReady is high. The component DONE compares the current value X_k with the next value to determine whether the computation can stop (whether X_k and X_k-1 are sufficiently close). If not, then the Xk register is loaded with the new value The division by 2 is achieved by removing the least significant bit and padding the left Register ax DIVIDE DONE Ready SORT CONTROL LA In this problem you will design the controller, SORT which controls the Divider and the two registers. The Dividers output is signal DiviReady goes high after a varying number of clock cycles It will hold the result until you assert its signal Distort controller asserts when Tool began ready when the and a Ready output your controller has a which the computation received new computation. The result is made available on output ski until another is Design the control for this computation (SORT CONTROL) a. Draw the state diagram b Make a table equations for your the Brachiated assuming a one-hot state encoding c. obtain the next-state and output