Build a linear optimization routine that returns the most cost efficient method to supply the processing sites with biomass. the solution should indicate how much biomass will be drawn from each forest, how much biomass will be processed at each site, and the objective function value.

- I believe solver is what is needed just not sure how to do it.

- Thank you for the help

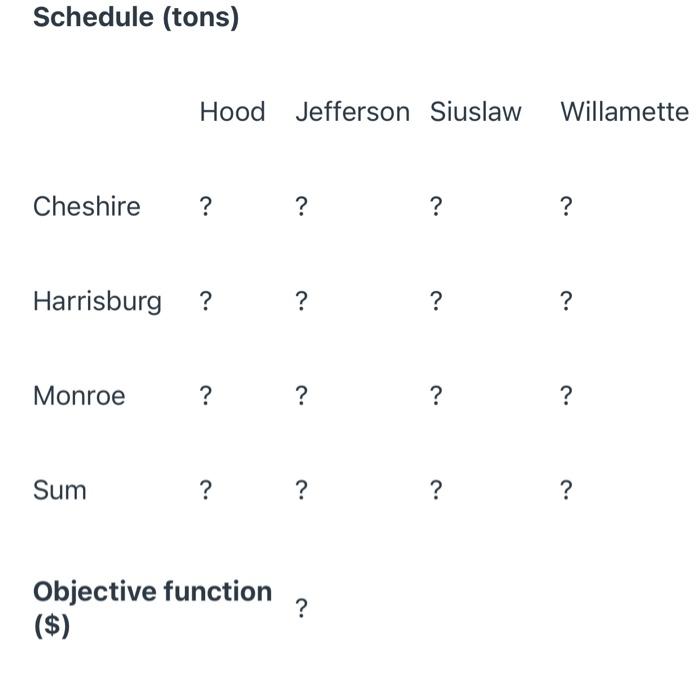
An organization manages four forests named Hood, Jefferson, Siuslaw, and Willamette. The organization also operates three biomass processing sites named Cheshire, Harrisburg, and Monroe that process biomass from the forests. The maximum biomass production capacity (supply) from each forest in tons per month is listed below. Forest Biomass (tons/month). Hood 85 Jefferson 95 Siuslaw 80 Willamette 70 The minimum amount of biomass (demand) in tons per month that is necessary for each processing site to maintain operations is listed below. Processing site Biomass processing monthly requirement (tons/month). Cheshire 65 Harrisburg 75 Monroe 80 The cost ($) of transporting biomass from the forests to the processing sites per ton is listed below. From: Hood Jefferson Siuslaw Willamette To: Cheshire 270 220 170 195 Harrisburg 245 195 270 270 Monroe 170 195 270 320 Build a linear optimization routine that returns the most cost efficient method to supply the processing sites with biomass. Your solution should clearly indicate how much biomass will be drawn from each forest, how much biomass will be processed at each site, and the objective function value. Your worksheet should be labeled Problem 1. Schedule (tons) Hood Jefferson Siuslaw Willamette Cheshire ? ? ? ? ? Harrisburg ? ? ? ? Monroe ? ? ? ? Sum ? ? ? ? Objective function ($) ? An organization manages four forests named Hood, Jefferson, Siuslaw, and Willamette. The organization also operates three biomass processing sites named Cheshire, Harrisburg, and Monroe that process biomass from the forests. The maximum biomass production capacity (supply) from each forest in tons per month is listed below. Forest Biomass (tons/month). Hood 85 Jefferson 95 Siuslaw 80 Willamette 70 The minimum amount of biomass (demand) in tons per month that is necessary for each processing site to maintain operations is listed below. Processing site Biomass processing monthly requirement (tons/month). Cheshire 65 Harrisburg 75 Monroe 80 The cost ($) of transporting biomass from the forests to the processing sites per ton is listed below. From: Hood Jefferson Siuslaw Willamette To: Cheshire 270 220 170 195 Harrisburg 245 195 270 270 Monroe 170 195 270 320 Build a linear optimization routine that returns the most cost efficient method to supply the processing sites with biomass. Your solution should clearly indicate how much biomass will be drawn from each forest, how much biomass will be processed at each site, and the objective function value. Your worksheet should be labeled Problem 1. Schedule (tons) Hood Jefferson Siuslaw Willamette Cheshire ? ? ? ? ? Harrisburg ? ? ? ? Monroe ? ? ? ? Sum ? ? ? ? Objective function ($)