Business Intelligence from Big Data

Prescriptive Analytics: Optimization and Simulation

Multi-Part Question on Linear Programming

***YOU MUST USE MICROSOFT EXCEL TO DO THIS PROBLEM.

For dollar amount, answer in two (2) decimal points (e.g. 35.32). For quantity, answer in whole number (e.g. 4567). Blackwood Manufacturing has two production plants, one is in Henderson and the other one is in Sun Valley. The company is specialized in making gel ink rollerball pens. Once the products are manufactured, they are shipped to their close-by warehouses for storage. The first warehouse is located in the city of Las Vegas and can store up to 375 lots. The second warehouse is located in the city of Reno and can store up to 700 lots. The shipping cost per lot among the locations are given in the two tables below.

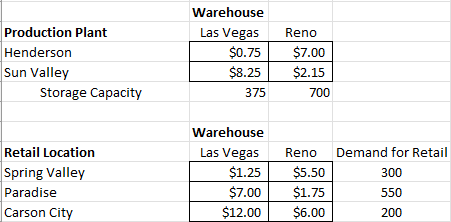
The products from the two warehouse locations then can be requested to be shipped to different retail locations. Blackwood has three retail stores, one is in Spring Valley, one is in Paradise and one is in Carson City. The demands for the three locations are 300, 550 and 200.

For each of these parts, you either fill in the blank (i.e. _) or select an answer from options provided (i.e. [option 1 OR option 2]) to you. The company is interesting in saving costs. Use Excel Solver to model the above problem and answer the following:

1. The total shipping cost from the plants to the warehouses is _.
2. The total shipping cost from the warehouses to the retail locations is _.
3. The overall total shipping costs is _.
4. The number of lots shipped from Las Vegas warehouse to the retail location in Paradise is _.
5. The number of lots left in the Las Vegas warehouse is _.
6. The number of lots left in the Reno warehouse is _.

If you can change the capacity of one of the warehouses (e.g. add 1 unit to the right-hand-side), which one would you recommend to change in this problem that would most benefit the company? (7) [Las Vegas OR Reno]. This is because the shadow price for the constraint is (8) [zero, positive, OR negative] which means that the company (9) [loses OR saves] (10) _ dollars for every additional unit added to the right-hand-side, up to (11) _ maximum quantity. Otherwise, we need to solve for a new solution.

If you must increase the demand of one of the retail locations (e.g. add 1 unit to the right-hand-side), which one would you recommend the company to avoid increasing in this problem that would most benefit the company? (12) [Spring Valley, Paradise, OR Carson City]. This is because the shadow price for the constraint is (13) [negative, zero, OR positive] which means that the company (14) [saves OR loses] (15) _ dollars for every additional unit added to the right-hand-side.

NOTE: - You should have 2 sets of decision variables: the quantities being shipped from production plants to the two warehouses and the quantities being shipped from the warehouses to the retail locations. (Hint: use a comma to separate the 2 sets of decision variables in the By changing variable cells in Solver Parameters). - Quantities shipped to the warehouse must be met, no more or less. - At the minimum, demands from the different retail locations must be met. - Quantities shipped from the different warehouses cannot be more than their available quantities.

\begin{tabular}{|c|c|c|c|} \hline & Warehouse & & \\ \hline Production Plant & Las Vegas & Reno & \\ \hline Henderson & \begin{tabular}{l} $0.75 \\ \end{tabular} & $7.00 & \\ \hline Sun Valley & $8.25 & $2.15 & \\ \hline \multirow[t]{2}{*}{ Storage Capacity } & 375 & 700 & \\ \hline & Warehouse & & \\ \hline Retail Location & Las Vegas & Reno & Demand for Retail \\ \hline Spring Valley & $1.25 & $5.50 & 300 \\ \hline Paradise & $7.00 & $1.75 & 550 \\ \hline Carson City & $12.00 & $6.00 & 200 \\ \hline \end{tabular}