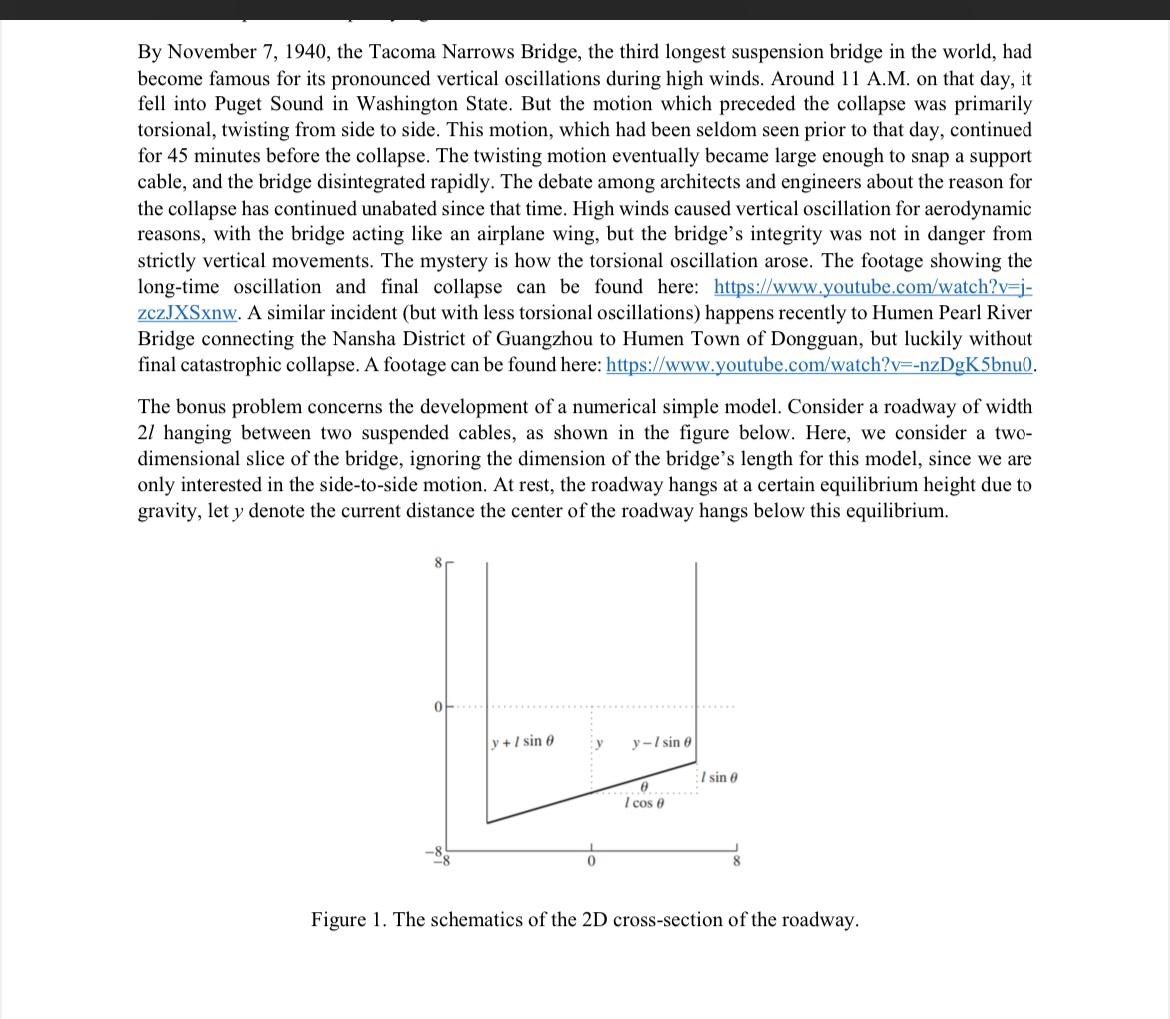
By November 7, 1940, the Tacoma Narrows Bridge, the third longest suspension bridge in the world, had become famous for its pronounced vertical oscillations during high winds. Around 11A.M. on that day, it fell into Puget Sound in Washington State. But the motion which preceded the collapse was primarily torsional, twisting from side to side. This motion, which had been seldom seen prior to that day, continued for 45 minutes before the collapse. The twisting motion eventually became large enough to snap a support cable, and the bridge disintegrated rapidly. The debate among architects and engineers about the reason for the collapse has continued unabated since that time. High winds caused vertical oscillation for aerodynamic reasons, with the bridge acting like an airplane wing, but the bridge's integrity was not in danger from strictly vertical movements. The mystery is how the torsional oscillation arose. The footage showing the long-time oscillation and final collapse can be found here: zczJXSxnw. A similar incident (but with less torsional oscillations) happens recently to Humen Pearl River Bridge connecting the Nansha District of Guangzhou to Humen Town of Dongguan, but luckily without final catastrophic collapse. A footage can be found here: https://www.youtube.com/watch? v=-nzDgK 5bnu0. The bonus problem concerns the development of a numerical simple model. Consider a roadway of width 2l hanging between two suspended cables, as shown in the figure below. Here, we consider a twodimensional slice of the bridge, ignoring the dimension of the bridge's length for this model, since we are only interested in the side-to-side motion. At rest, the roadway hangs at a certain equilibrium height due to gravity, let y denote the current distance the center of the roadway hangs below this equilibrium. Figure 1. The schematics of the 2D cross-section of the roadway. Two suspension cables are stretched ylsin and y+lsin from equilibrium (c.f. Figure 1), respectively. Hooke's law postulates a linear response, meaning that the restoring force the cables apply will be proportional to the deviation, namely, f(y)=Ky. Due to the fact that the bridge material is non-homogenous and does not behave linearly, thus, here we use a non-linear restoring forcing term: f(y)=(K/a)(ev1). Assume that a linear viscous damping term, dy ' is given that is proportional to the translational velocity, where d is the damping coefficient and y is the translational velocity of the bridge. The Newton second law results in two ODEs for y and , respectively: y=dymaK[ea(ylsin)1+ea(y+lsin)1]=d+l3cosmaK[ea(ylsin)ea(y+lsin)] (1) Derive using Newton second law for the two ODEs for y and . (2) As the equations stand, the state y=y===0 is an equilibrium. Now turn on the wind. Assume that the wind forcing term is 0.2Wsint to be added to the right-hand side of the y equation, where W is the wind speed in km/hr. This adds a strictly vertical oscillation to the bridge. Useful estimates for the physical constants can be made. The mass of a one-foot length of roadway was about 2500kg, and the spring constant K has been estimated at 1000N. The roadway was about 12 meters wide. For this simulation, the damping coefficient was set at d=0.01, and the Hooke's nonlinearity coefficient a=0.2. An observer counted 38 vertical oscillations of the bridge in one minute shortly before the collapse - set =2(38/60). These coefficients are only guesses, but they suffice to show ranges of motion that tend to match photographic evidence of the bridge's final oscillations. Run tacoma.m with wind speed W=80km/hr and initial conditions y=y==0,=0.001. The bridge is stable in the torsional dimension if small disturbances in die out; unstable if they grow far beyond original size. Which occurs for this value of W ? (3) Replace the Trapezoid Method by fourth-order Runge-Kutta to improve accuracy. Also, add new figure windows to plot y(t) and (t). (4) The system is torsionally stable for W=50km/hr. Find the magnification factor for a small initial angle. That is, set (0)=104 and find the ratio of the maximum angle (t),0t