By Octave, Who can help me?

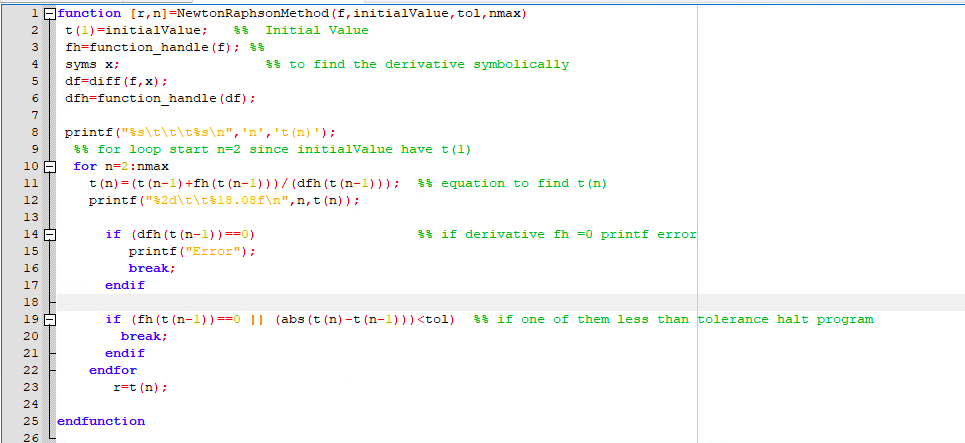
Computing - Newton-Raphson Method In this lab you will write a routine which implements the Newton-Raphson Method. Your m-file will accept as input a function, an initial value, a tolerance and a max number of iterations, and will output an estimate for the root within the tolerance, or an error message if the max number of iterations has been reached. Since the m-file accepts only the function and not its derivative, the m-file will need to compute the derivative symbolically. 1. (80 points) At the command line type pkg load symbolic but do not type in syms initpython as we did last time. Initialize a symbolic variable r: syms x and then follow the instructions below to write an m-file implementing the Newton-Raphson Method, run it, and drop a single properly-named diary file in Moodle. Name the m-file NewtonRaphsonMethod.m. (a) Your m-file must accept as input 1) a symbolic function f defined as (note - no anonymous functions this time - no @) f=x*3-2*x*2-6 2) an initial value, 3) a tolerance (use 10-8) and 4) the max number of iterations (use nmax = 100). The output (left unprinted by use of the semicolon) will be the approximate root and the number of iterations needed to calculate it. (b) Since x is a symbolic variable, our iterates will be t(1), t(2), .... In the m-file, below the function definition line and the documentation see Problem 2), initialize t: t(1)-initialvalue; (c) To make way for computing f(tn) we type fh=function_handle(f) so that f(tn) can be computed as fh(t(n)). (d) To find the derivative symbolically in the m-file we type syms x and df-diff(f,x), and similarly to fh we type dfh=function_handle(af). (e) Now we are ready for the loop. We start the loop at n = 2 since we already have t(1). In each iteration of the loop we i. check to see if dfh(t(n-1))==0 and if so print a clearly explained error message, otherwise ii. assign a value to In according to Equation 2.3.1, iii. check whether In is an actual root, and check whether En is an ap- proximate root using abs(t(n)-t (n-1)), and iv. generate a printed row of values of n and xn from your loop by us- ing appropriate printf statements taking into account the specified tolerance, as part of a table with column headers. (f) After the routine exits the loop for whichever reason, assign r = t(n) for the output and perform the usual n = nmax check. Remember that n = nmax does not necessarily mean that we don't have a good approximation! So, calculate f(a) for the user's sake and include a final printf statement "The best approximation to within is for which f(r) =." (g) Test your program on these benchmark functions and initial values: i. f with f(x) = r - 2.2 - 6, Xo = 2 ii. f with f(x) = I-COSI, 10 = 2 iii. f with f(x)=r', zo=1 iv. (Two initial values) f with f(1) = (1 - 2)2 - Inx, = 1.3, 30 = 3.3 v. (Two initial values) f with f(x) = 6-3-2 +5 cos -7, 10 = 1.6, 10 = 1.5 vi. f with f(x) = x + cos r, 10 = /2+.01, Xo = /2-.01 MO 1 Q function (r, n] =NewtonRaphsonMethod(f, initialValue, tol, nmax) t(1)=initialValue; $$ Initial Value fh=function_handle(f); $$ syms x; $$ to find the derivative symbolically df=diff(f,x); dfh=function_handle (df); 10 11 printf("%s\t\t\tss ", 'n','t (n)'); *% for loop start n=2 since initialValue have t(1) for n=2 : nmax t(n)=(t (n-1) +fh (t (n-1)))/(dfh (t (n-1))); $$ equation to find tan) printf("%d\t\t$18.08 ", n, t(n)); 1 *$ if derivative fh =0 printf error if (dfh(t (n-1))==0) printf("Error"); break; endif $$ if one of them less than tolerance halt program ET if (fh(t (n-1))==0 || (abs(t (n)-t (n-1)))