C++ code (xcode mac equivalent) to the following assignment below. Read carefully and follow instructions on page.

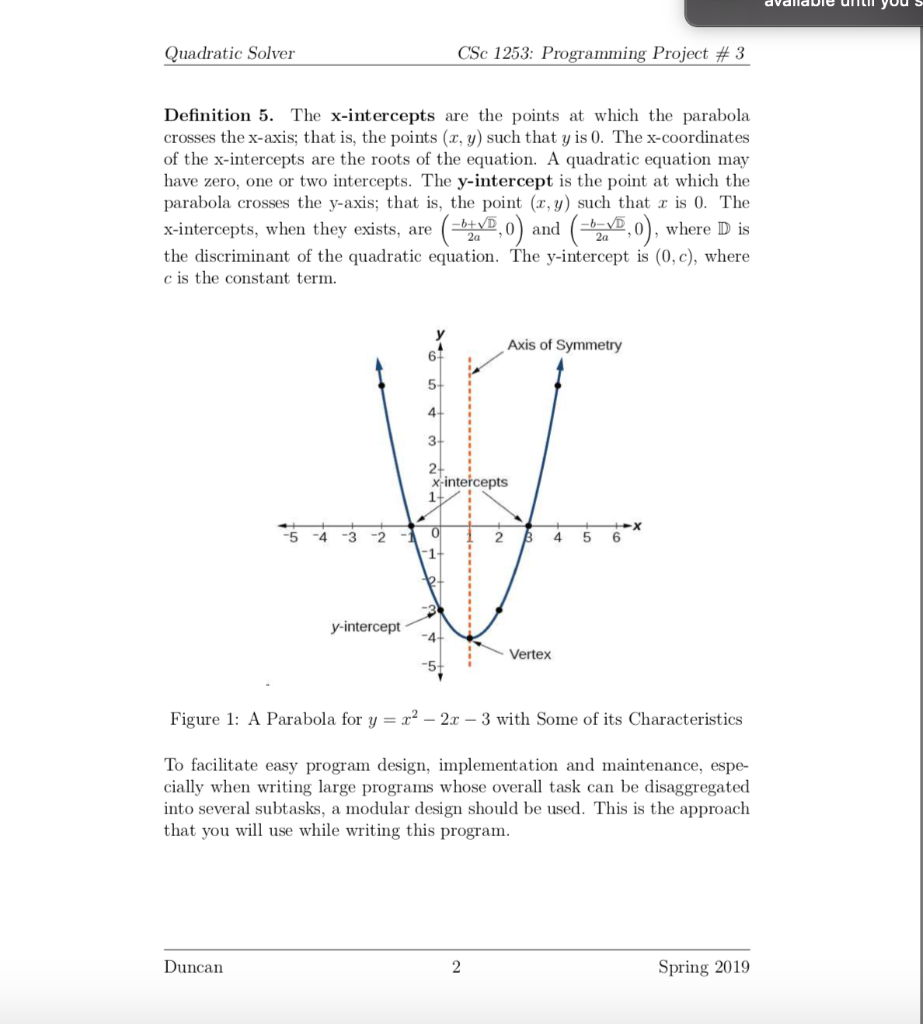
Quadratic Solver CSc 1253: Programming Project # 3 Solving Quadratic Equations Out: 2/26 Due: 3/11 by 11:50 PM Learning Objectives Modular Programming, Implementing Value-returning Functions, and Implementing Void Functions Definition 1. A Quadratic Equation is a second-order polynomial equa tion in a single variable r ar2 + br + c = 0 with a f 0. a is referred to as the coefficient of the quadratic term, b, the coefficient of the linear term. and c, the constant term. Because a quadratic equation is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has two solutions. These solutions may both be real or complex Definition 2. The quantity D=b2-4ac is called the discriminant of a quadratic equation Definition 3. The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. Given any horizontal line that intersects the parabola at two points, both points are equidistant from the axis of symmetry. The axis of symmetry of a parabola is the vertica line Definition 4. A vertex of a parabola is the point at which it crosses the axis of symmetry. It is the lowest point (minimm when the parabola is concave upward and the highest point (maximum) when it is concave downward. The vertex of a parabola is the point ( 2 -c Duncan Spring 2019 Quadratic Solver CSc 1253: Programming Project # 3 Definition 5. The x-intercepts are the points at which the parabola crosses the x-axis; that is, the points (x, y) such that y is 0. The x-coordinates of the x-intercepts are the roots of the equation. A quadratic equation may have zero, one or two intercepts. The y-intercept is the point at which the parabola crosses the y-axis; that is, the point (x, y) such that r is 0. The x-intercepts, when they exists, are the discriminant of the quadratic equation. The y-intercept is (0, c), where c is the constant term. 2here D is Axis of Symmetry 6 x-intercepts 5 4 3 2 2 4 5 6 y intercept 4 Vertex Figure 1: A Parabola for y r2-2r - 3 with Some of its Characteristics To facilitate easy program design, implementation and maintenance, espe- cially when writing large programs whose overall task can be disaggregated into several subtasks, a modular design should be used. This is the approach that you will use while writing this program Duncan Spring 2019