C language ICS 103

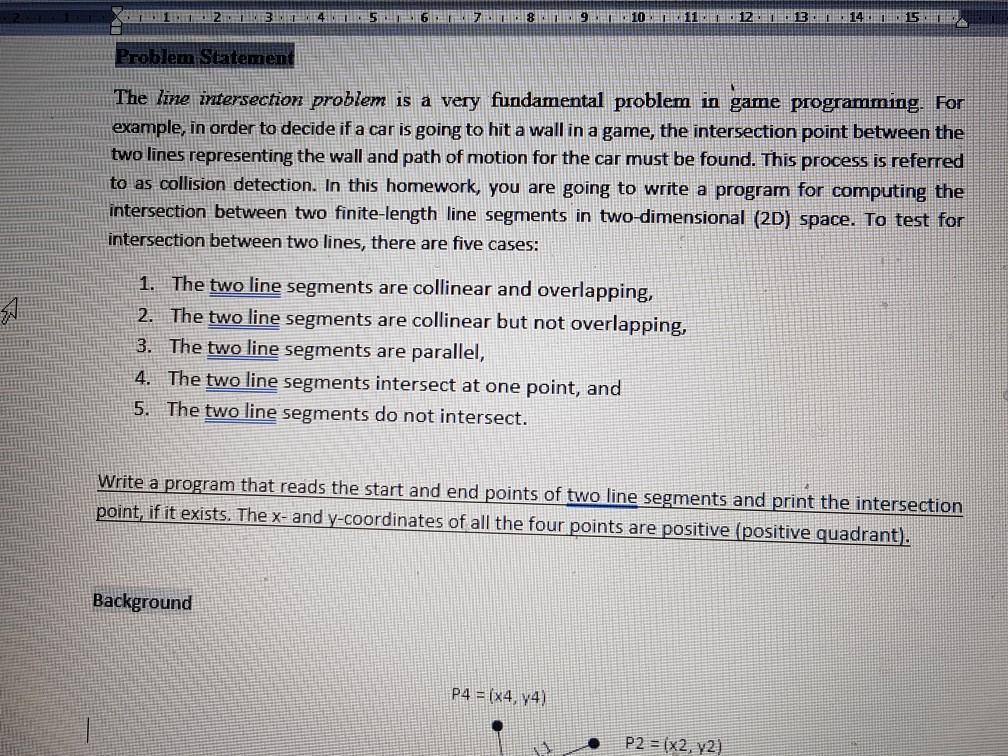
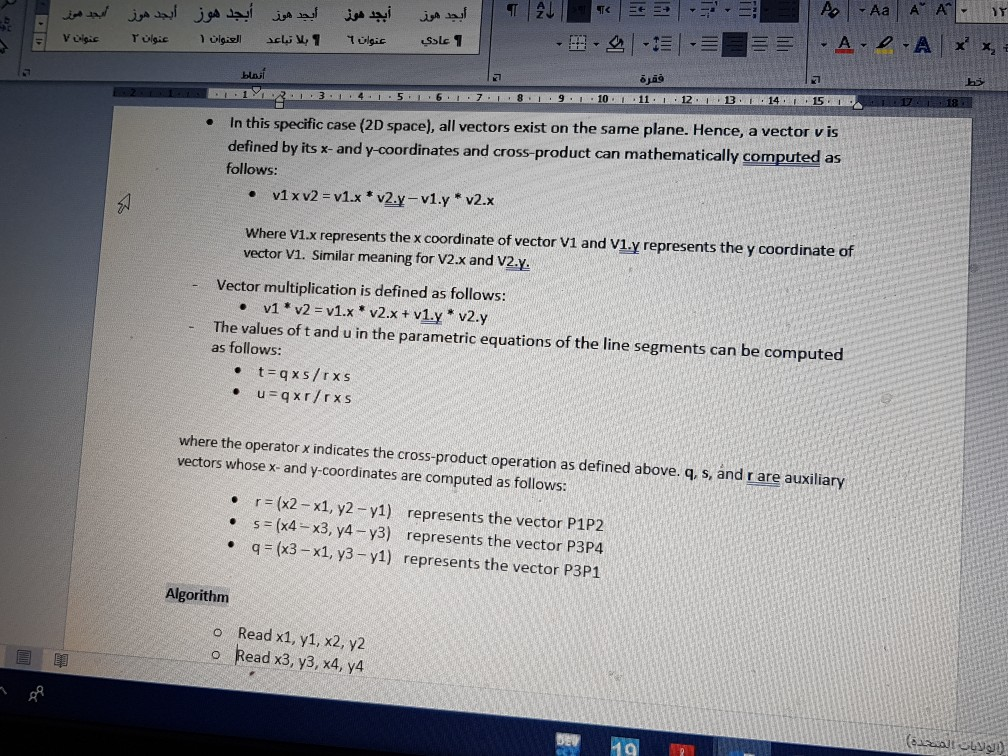
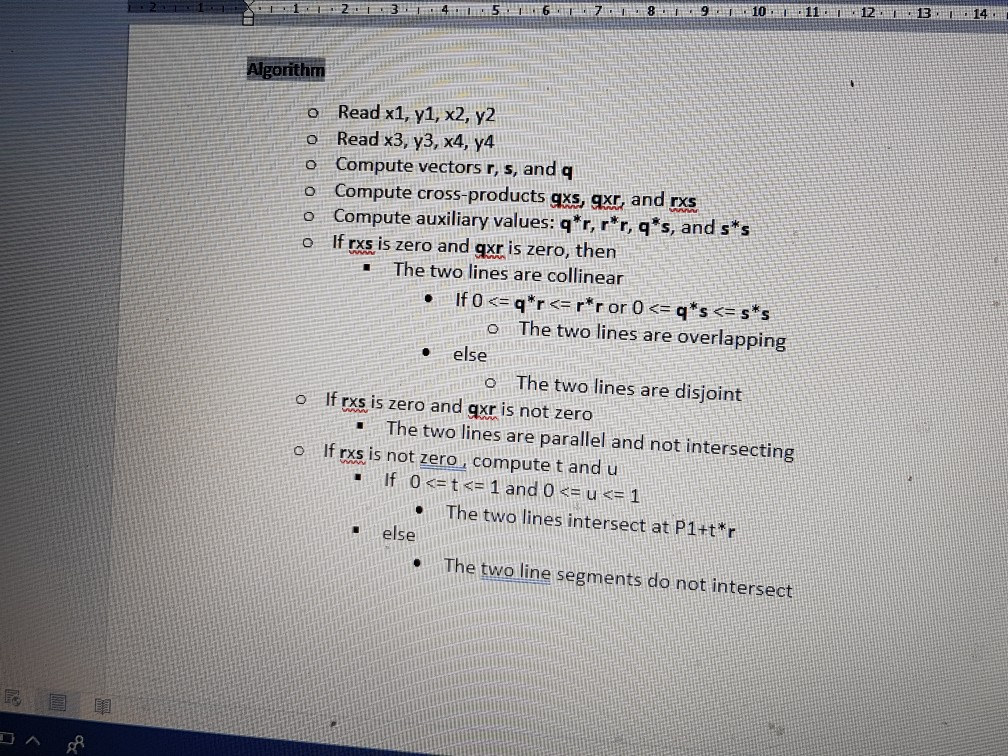
12EB 15 lerm Statem The line intersection problem is a very fundamental problem in game programming. For example, in order to decide if a car is going to hit a wall in a game, the intersection point between the two lines representing the wall and path of motion for the car must be found. This process is referred to as collision detection. In this homework, you are going to write a program for computing the intersection between two finite -length line segments in two-dimensional (2D) space. To test for intersection between two lines, there are five cases: 1. The two line segments are collinear and overlapping 2. The two line segments are collinear but not overlapping, 3. The two line segments are parallel 4. The two line segments intersect at one point, anc 5. The two line segments do not intersect Write a program that reads the start and end points of two line segments and print the intersection point if it exists. The x and y-coordinates of all the four points are positive (positive quadrant). Background P4 -(x4, y4) P2 = (x2, y2 in P4 (x4, y4) P2 = (x2, y2) L2 P3 (x3, y3 The two line segments lie in the positive quadrant. Therefore, the x- and y-coordinates of their end points are all positive. In the example above, the two line segments L1 and 12 can mathematically characterized using the following two parametric equations respectively: 11(x, y) (x1, y1)+t (x2-x1, y2 y1) 12t%, y) (x3, y3) + u*(x4- x3, y4-y3) where t e [O11 and u e [0.1]. The points P1(xl, y1) and P2(x2, y2) are the end points for line 1 (11) The points P3(x3, y3) and P4lx4, y4) are the end points for line 2 (12) A 2D vector is defined by two points. For example, a vector v whose tail is at the origin and its head at point (5, 7 is represented as follows . (5,7 12 3 14 15 101 11 In this specific case (2D space), all vectors exist on the same plane. Hence, a vector v is defined by its x- and y-coordinates and cross-product can mathematically computed as follows: . Where V1.x represents the x coordinate of vector V1 and v1.y represents the y coordinate of vector V1. Similar meaning for V2.x and V2y. Vector multiplication is defined as follows: v1 v2 v1.x v2.x + v1y v2.y The values of t and u in the parametric equations of the line segments can be computed as follows: - where the operator x indicates the cross-product operation as defined above. q, s, nd r are auxiliary vectors whose x- and y-coordinates are computed as follows: . r (x2 -x1, y2 y1) represents the vector P1P2 (x4 x3, y4 -y3) represents the vector P3P4 .q (x3-x1, y3 -y1) represents the vector P3P1 Algorithm o Readx1, y1, x2, y2 o Read x3, y3, x4, y4 10 11 12 13 5 6 89 Algorithm o Read x1, y1, x2, y2 o Read x3, y3, x4, y o Compute vectors r, s, and q o Compute cross-products gxs, gxr, and rxs o Compute auxiliary values: q'r, r*r, q's, and ss o If rxs is zero and gxr is zero, then The two lines are collinear o The two lines are overlapping else o The two lines are disjoint If rxs is zero and gxr is not zero o .The two lines are parallel and not intersectinig o If rxs is not zero compute t and u If 0