Question: C++ -------------- --------------------------------------------------- main.cpp source code ------------------------------------------------------------------------------------------------ Overview In the source code file provided: complete the missing subroutine for calculating the mean of the integer
C++ --------------



--------------------------------------------------- main.cpp source code ------------------------------------------------------------------------------------------------
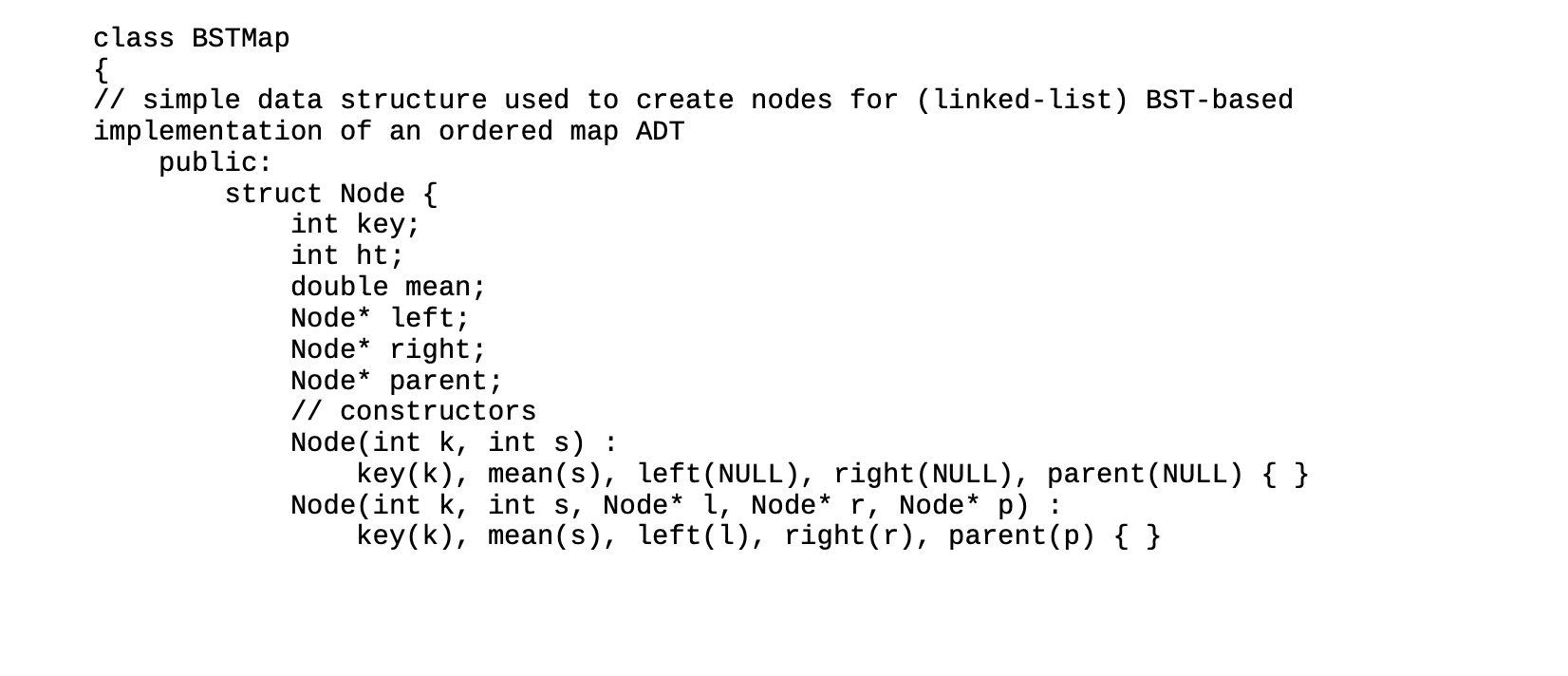







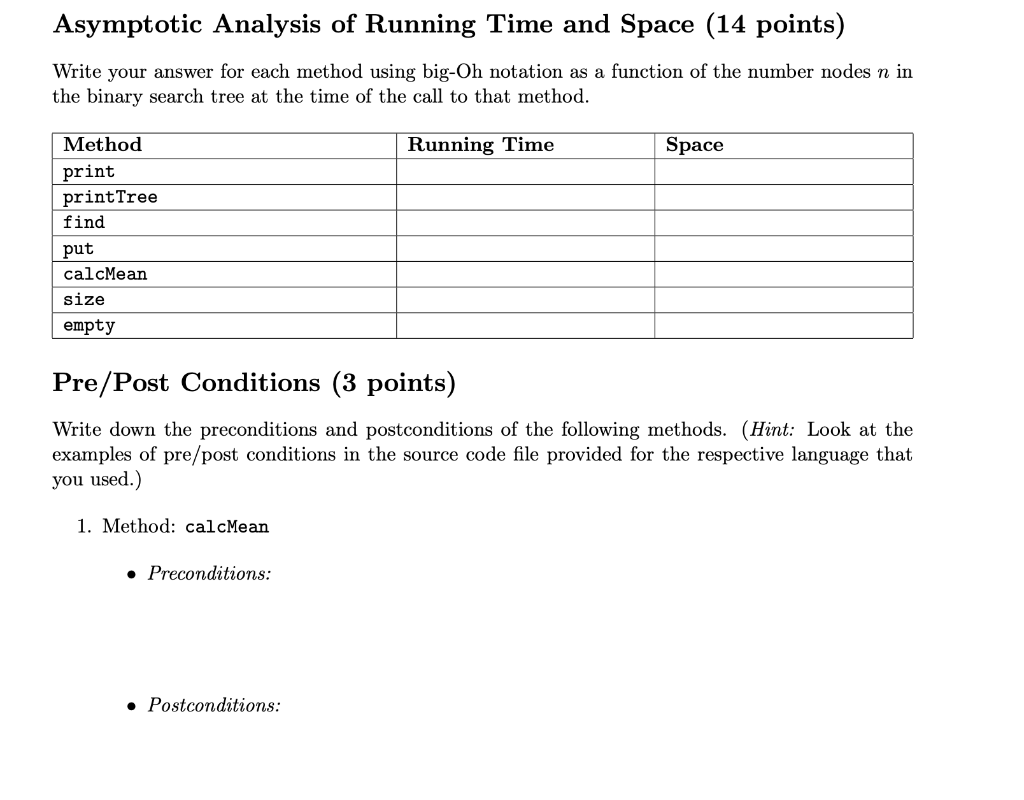
Overview In the source code file provided: complete the missing subroutine for calculating the mean of the integer keys in a binary search tree. In the memo file provided: - write down the preconditions and postconditions of those operations provide a worst-case running time and space, using big-Oh notation as function of the number of nodes n in the BST, which roughly characterizes the input size of certain methods used in the implementation Program Implementation In class we briefly reviewed binary search trees (BSTs). Although BSTs have some drawbacks from an algorithmic standpoint, they are still a great starting point for building more sophisticated data structures, which we will learn about soon. In this first project, you are asked to implement an algorithm which, given a BST with integer keys, computes the mean of all entries in the tree (and every sub-tree). The mean of a (sub) tree rooted at Node s is defined as the mean of all the integer keys contained in that sub-tree, including s. The Node object has a member called mean whose purpose is to hold the calculated mean of the sub-tree rooted at that Node. Source Code Details We will provide the source code for the BST implementation in three languages: C++, Java, and Python. This program constructs the relevant data structures for your algorithm implementations and handles input/output. However, the source will be missing the implementation for an important function. We expect you to complete the following function: calcMean: Calculates the mean of all keys contained in the (sub) tree rooted at s and saves the result to s.mean. This calculation is done for every Node in the (sub) tree. You are allowed to add additional functions, member variables, or even new classes, in order to aid in your implementation. You may also modify existing functions, but this should not be necessary to complete the program. You are not allowed to modify the input/output logic, or add extra input/output to the program, as this may interfere with the grading process. Input File Format and Sample File Use a file named input.txt, which is assumed to be located in the same subdirectory where the program is executed, to debug, test, and evaluate your implementation. Input File Format Each line in the input file can represent a single command to the program or multiple commands depending on the context. put Inserts a node into the BST for each key provided, but only if a node with that key doesn't already exist. mean Calculates the mean of all keys in every subtree in the BST, starting from the root print Display the current BST using a preorder/infix parenthetic representation: [, ] () print Tree Display the current BST using a representation which reflects the structure of the tree: right_child key:mean root key:mean left_child key:mean Sample Input File input.txt and Sample Output The following input file: put 12 6 20 2 9 15 22 mean printTree should produce the following output: put 12 6 20 2 9 15 22 mean printTree 22:22.00 20:19.00 15:15.00 12:12.29 9:9.00 6:5.67 2:2.00 Asymptotic Analysis of Running Time and Space (14 points) Write your answer for each method using big-Oh notation as a function of the number nodes n in the binary search tree at the time of the call to that method. Running Time Space Method print printTree find put calcMean size empty Pre/Post Conditions (3 points) Write down the preconditions and postconditions of the following methods. (Hint: Look at the examples of pre/post conditions in the source code file provided for the respective language that you used.) 1. Method: calcMean Preconditions: Postconditions: #include #include #include #include #include #include #include #include #include #include #include using namespace std; // Utility functions void loadFile(string fname, fstream& file) { file.open(fname.c_str(); if (file.fail() { cout key ":" mean left); cout right); cout printTree(s->right, space); cout key mean printTree(s->left, space); } // INPUT: a key k, as an integer // OUTPUT: a 2-element array, where // element o is w, the node with key k, if k is already in the ordered map, or NULL otherwise; and // element 1 is z, the parent of node w, or NULL if wis NULL or the root // or the last node visited while trying to find a node with key k in the BST BSTMap:: Node** BSTMap: :find(int k) const { Node* W = root; Node* z = NULL; // use BST property to determine where the node should be while (w && (w->key != k)) { z = w; // look in left or right subtree depending on key ordering W = (W->key > k) ? W->left : w->right; } Node** WAndz = new Node* [2]; WAndz[0] = w; WAndz[1] = z; return wAndz; } // INPUT: an integer key // OUTPUT: if k is already in the ordered map, then output the node containing k // otherwise, output the new node in the tree with the corresponding key k. // POSTCONDITION: a node with key k exists in the BST // if the BST was empty, then the new node becomes the root of the BST (and thus its only node) BSTMap:: Node* BSTMap::put(int k) { Node** wAndz = find(k); Node* W = WAndz[0]; Node* z = WAndZ[1]; // memory leak? delete wAndz; // already found if (w) { // usually would overwrite value but this BST doesn't have values return w; } // not found, then create new node and update tree Node* X = new Node(k, O, NULL, NULL, 2); if (z) { if (z->key > k) z->left = x; else z->right X; } else root = x; n++; if (n == 1) root = x; return x; } // INPUT: a pointer to a Node in the trees // PRECONDITION: memo // POSTCONDITION: memo void BSTMap::calcMean (Node* s) { // your code here } // OUTPUT: size of the tree int BSTMap: :size() const { return n; } // OUTPUT: true if the tree is empty; false otherwise bool BSTMap:: empty() const { return (!root); } int main() { string inputFilename = "input.txt"; string line; BSTMap B; // open input file fstream inputFile; loadFile(inputFilename, inputFile); while (getline(inputFile, line) { // trim whitespace // echo input cout tokens; while (getline(liness, token, ')). { // trim whitespace token.erase(token.find_last_not_of(" \t") + 1); tokens. push_back(token); } if (tokens.size() > 0) { // first token is the command command = tokens[0]; } else { command = ""; } == if (command "put") { // insert a node for each key specified for (unsigned int i = 1; i Inserts a node into the BST for each key provided, but only if a node with that key doesn't already exist. mean Calculates the mean of all keys in every subtree in the BST, starting from the root print Display the current BST using a preorder/infix parenthetic representation: [, ] () print Tree Display the current BST using a representation which reflects the structure of the tree: right_child key:mean root key:mean left_child key:mean Sample Input File input.txt and Sample Output The following input file: put 12 6 20 2 9 15 22 mean printTree should produce the following output: put 12 6 20 2 9 15 22 mean printTree 22:22.00 20:19.00 15:15.00 12:12.29 9:9.00 6:5.67 2:2.00 Asymptotic Analysis of Running Time and Space (14 points) Write your answer for each method using big-Oh notation as a function of the number nodes n in the binary search tree at the time of the call to that method. Running Time Space Method print printTree find put calcMean size empty Pre/Post Conditions (3 points) Write down the preconditions and postconditions of the following methods. (Hint: Look at the examples of pre/post conditions in the source code file provided for the respective language that you used.) 1. Method: calcMean Preconditions: Postconditions: #include #include #include #include #include #include #include #include #include #include #include using namespace std; // Utility functions void loadFile(string fname, fstream& file) { file.open(fname.c_str(); if (file.fail() { cout key ":" mean left); cout right); cout printTree(s->right, space); cout key mean printTree(s->left, space); } // INPUT: a key k, as an integer // OUTPUT: a 2-element array, where // element o is w, the node with key k, if k is already in the ordered map, or NULL otherwise; and // element 1 is z, the parent of node w, or NULL if wis NULL or the root // or the last node visited while trying to find a node with key k in the BST BSTMap:: Node** BSTMap: :find(int k) const { Node* W = root; Node* z = NULL; // use BST property to determine where the node should be while (w && (w->key != k)) { z = w; // look in left or right subtree depending on key ordering W = (W->key > k) ? W->left : w->right; } Node** WAndz = new Node* [2]; WAndz[0] = w; WAndz[1] = z; return wAndz; } // INPUT: an integer key // OUTPUT: if k is already in the ordered map, then output the node containing k // otherwise, output the new node in the tree with the corresponding key k. // POSTCONDITION: a node with key k exists in the BST // if the BST was empty, then the new node becomes the root of the BST (and thus its only node) BSTMap:: Node* BSTMap::put(int k) { Node** wAndz = find(k); Node* W = WAndz[0]; Node* z = WAndZ[1]; // memory leak? delete wAndz; // already found if (w) { // usually would overwrite value but this BST doesn't have values return w; } // not found, then create new node and update tree Node* X = new Node(k, O, NULL, NULL, 2); if (z) { if (z->key > k) z->left = x; else z->right X; } else root = x; n++; if (n == 1) root = x; return x; } // INPUT: a pointer to a Node in the trees // PRECONDITION: memo // POSTCONDITION: memo void BSTMap::calcMean (Node* s) { // your code here } // OUTPUT: size of the tree int BSTMap: :size() const { return n; } // OUTPUT: true if the tree is empty; false otherwise bool BSTMap:: empty() const { return (!root); } int main() { string inputFilename = "input.txt"; string line; BSTMap B; // open input file fstream inputFile; loadFile(inputFilename, inputFile); while (getline(inputFile, line) { // trim whitespace // echo input cout tokens; while (getline(liness, token, ')). { // trim whitespace token.erase(token.find_last_not_of(" \t") + 1); tokens. push_back(token); } if (tokens.size() > 0) { // first token is the command command = tokens[0]; } else { command = ""; } == if (command "put") { // insert a node for each key specified for (unsigned int i = 1; i

















