c++

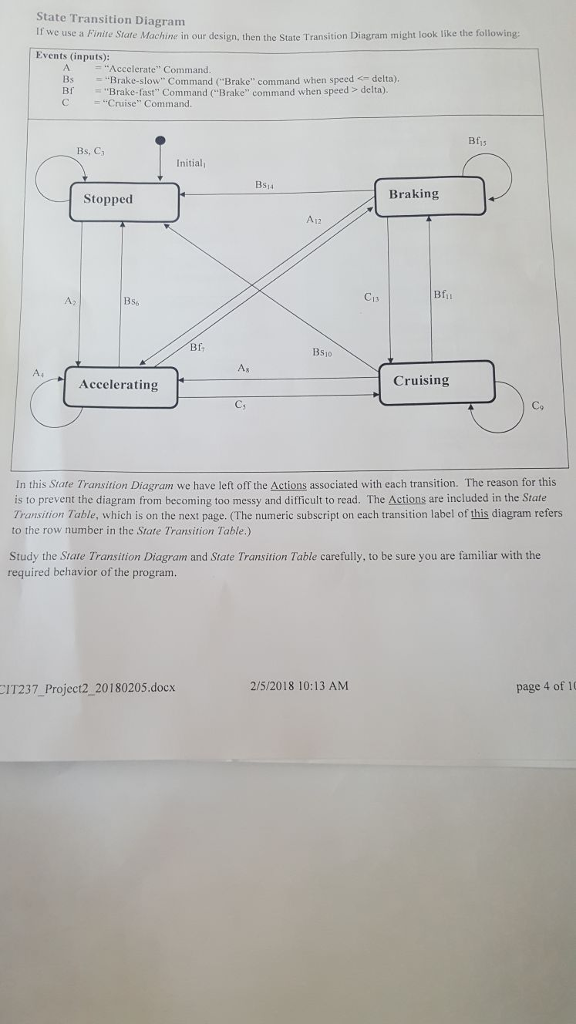
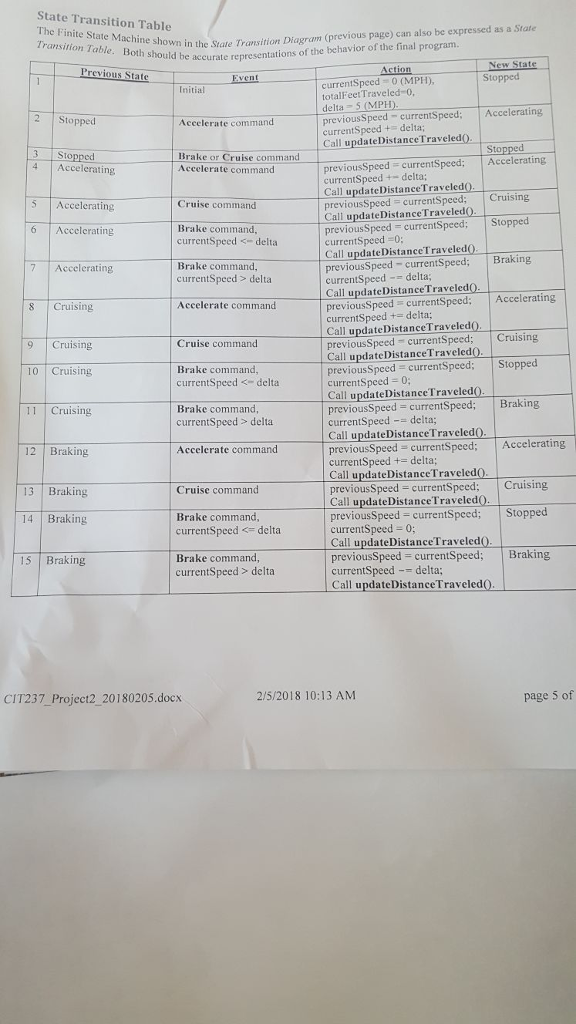
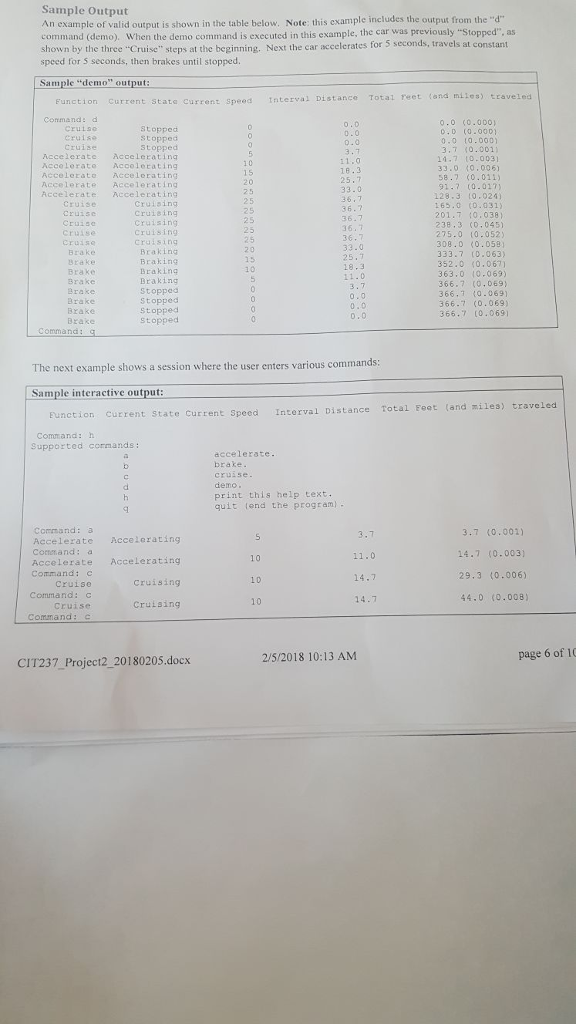
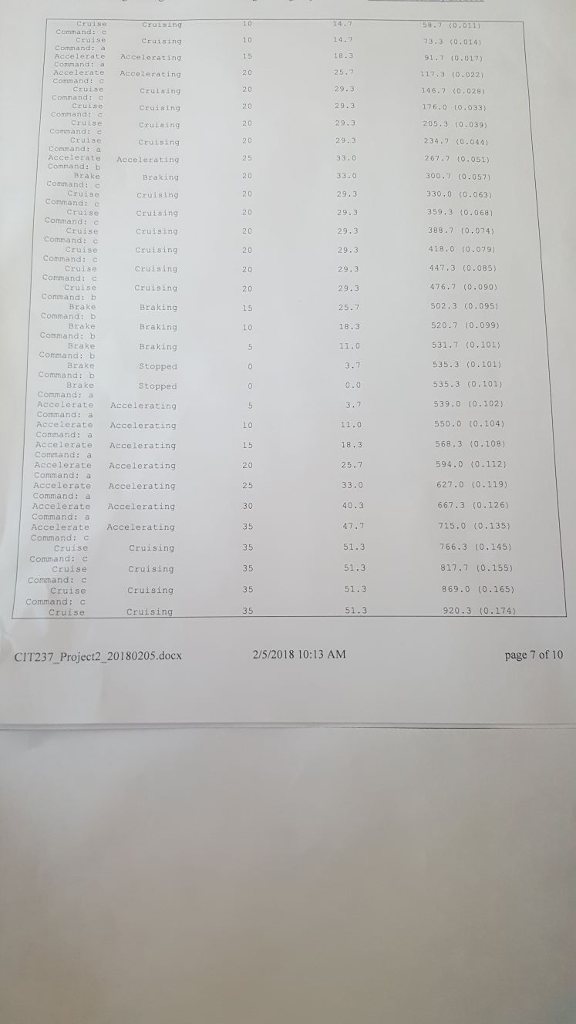
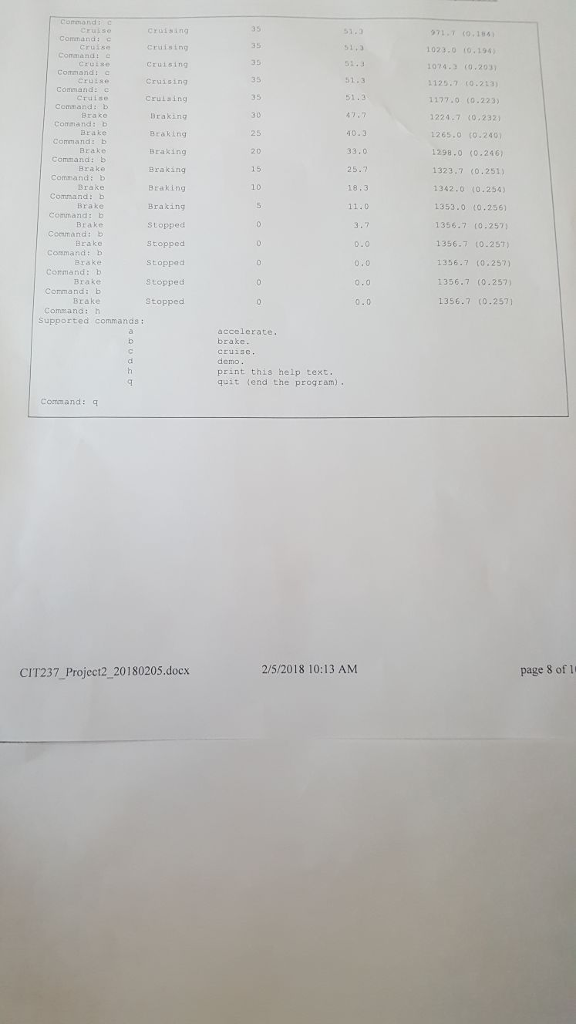
Overview Automobile Speed/Distance Application Program This programming project involves creating a C++ program which simulates the speed of a car distance traveled over a period of time. This should be an interactive program w the user and produces text output on the console. Each command entered by the user and calculates the hich accepts keyboa rd input from For example, the a" (accelerate) command should increase the speed by 5 miles per hour (MPH) over nd. Similarly, the "b" (brake) command should decrease the speed by 5 MPH over a time a time interval of 1 seco of 1 second, and the "e" (cruise) command should keep the speed constant for 1 second. All of these operations include calculation of how far the car travels during the I second interval, and the total distance aveled since the program started. A separate "d" (demo) command outputs a sequence of steps, similar to that in the sample data, simply by executing the other operations in a predetermined sequence. This document discusses the requirements for the program, as well as possible implementation details. Be sure you understand this document before you begin coding your final solution. General Discussion of the Project Imagine a car which starts out "Stopped", at some initial position. We could say that the car is at "position zero and its current speed is zero Miles-per-hour. If the driver of the car does nothing, then the car will remain at its initial position. However, if the driver steps on the gas pedal, the car will "accelerate": its speed will increase by some amount. Now that the car is moving, its position will change over time. How much will the position change? This depends on the speed, and how much time has clapsed. It turns out that a car moving at a constant speed of 25 miles per hour (36.7 feet per second) will travel 367 feet in 1o seconds. (Multiply 36.7 feet per second times 10 seconds.) But what if the speed is not constant? In this case we need to know the average speed over the specified time interval. If the speed changes at a constant rate, perhaps 5 miles-per-hour each second, then the average the speed at the beginning of the time interval (previousSpeed), plus the speed at the end of the time interval speed is (currentspeed), divided by 2: averagespeed = (previousSpeed + currentSpeed) / 2; averages peedFeet PerSeco nd-averagespeed * 5280,0/3600.0; interva ! Fee tTraveled averageSpeedFeetPerSecond * time Interval; = - For convenience, we can keep the timeInterval value fixed at one second. The calculations described above mention speed in "miles per hour" and distance in "feet". This is deliberate, fo aesthetic reasons: people are accustomed to thinking of the speed of a car in "miles per hour", at least in the United States. Yet, if we were to express the distance traveled over a few seconds in miles, th would be tiny fractions of a mile, and would therefore not be intuitively appropriate to the person using the en the numbers 2/5/2018 10:13 AM page 1 o CIT237_Project2 20180205.docx Overview Automobile Speed/Distance Application Program This programming project involves creating a C++ program which simulates the speed of a car distance traveled over a period of time. This should be an interactive program w the user and produces text output on the console. Each command entered by the user and calculates the hich accepts keyboa rd input from For example, the a" (accelerate) command should increase the speed by 5 miles per hour (MPH) over nd. Similarly, the "b" (brake) command should decrease the speed by 5 MPH over a time a time interval of 1 seco of 1 second, and the "e" (cruise) command should keep the speed constant for 1 second. All of these operations include calculation of how far the car travels during the I second interval, and the total distance aveled since the program started. A separate "d" (demo) command outputs a sequence of steps, similar to that in the sample data, simply by executing the other operations in a predetermined sequence. This document discusses the requirements for the program, as well as possible implementation details. Be sure you understand this document before you begin coding your final solution. General Discussion of the Project Imagine a car which starts out "Stopped", at some initial position. We could say that the car is at "position zero and its current speed is zero Miles-per-hour. If the driver of the car does nothing, then the car will remain at its initial position. However, if the driver steps on the gas pedal, the car will "accelerate": its speed will increase by some amount. Now that the car is moving, its position will change over time. How much will the position change? This depends on the speed, and how much time has clapsed. It turns out that a car moving at a constant speed of 25 miles per hour (36.7 feet per second) will travel 367 feet in 1o seconds. (Multiply 36.7 feet per second times 10 seconds.) But what if the speed is not constant? In this case we need to know the average speed over the specified time interval. If the speed changes at a constant rate, perhaps 5 miles-per-hour each second, then the average the speed at the beginning of the time interval (previousSpeed), plus the speed at the end of the time interval speed is (currentspeed), divided by 2: averagespeed = (previousSpeed + currentSpeed) / 2; averages peedFeet PerSeco nd-averagespeed * 5280,0/3600.0; interva ! Fee tTraveled averageSpeedFeetPerSecond * time Interval; = - For convenience, we can keep the timeInterval value fixed at one second. The calculations described above mention speed in "miles per hour" and distance in "feet". This is deliberate, fo aesthetic reasons: people are accustomed to thinking of the speed of a car in "miles per hour", at least in the United States. Yet, if we were to express the distance traveled over a few seconds in miles, th would be tiny fractions of a mile, and would therefore not be intuitively appropriate to the person using the en the numbers 2/5/2018 10:13 AM page 1 o CIT237_Project2 20180205.docx