C PROGRAMMING QUESTION. H im having trouble writing a c program to solve the linear convection equation in 1D. I have coded it in python and the code is below for reference. I am trying to rewrite it in C without any luck. Any help would be greatly appreciated

THIS IS THE WORKING PYTHON CODE TO HELP WITH THE C PROGRAM
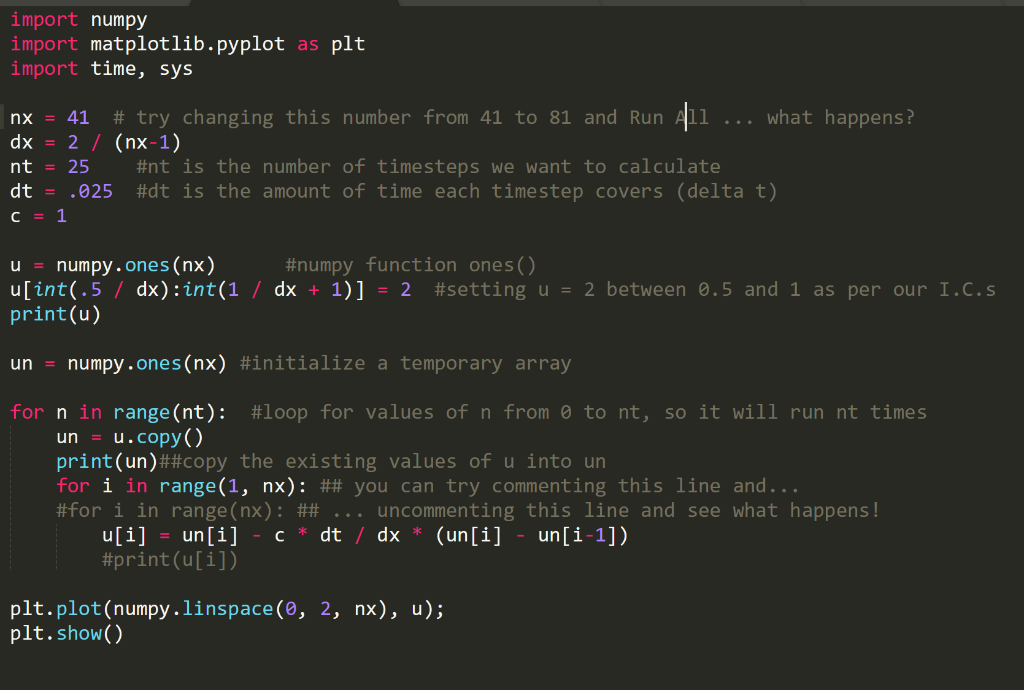
The 1-D Linear Convection equation is the simplest, most basic model that can be used to learn something about CFD. It is surprising that this little equation can teach us so much! Here it is: da + c ot = 0 With given initial conditions (understood as a wave), the equation represents the propagation of that initial wave with speed c, without change of shape. Let the initial condition be u(x, 0) = ug(x). Then the exact solution of the equation is u(x, t) = u((x ct). We discretize this equation in both space and time, using the Forward Difference scheme for the time derivative and the Backward Difference scheme for the space derivative. Consider discretizing the spatial coordinate x into points that we index from i = 0 to N, and stepping in discrete time intervals of size At. From the definition of a derivative (and simply removing the limit), we know that: u(x) u(x + 4x) x Our discrete equation, then, is: in + 1 u u - u? to = 0 At x Where n and n + 1 are two consecutive steps in time, while i 1 and are two neighboring points of the discretized x coordinate. If there are given initial conditions, then the only unknown in this discretization is u? + 1. We can solve for our unknown to get an equation that allows us to advance in time, as follows: u" + 1 = c) = u? CA (u" " - 1) import numpy import matplotlib.pyplot as plt import time, sys nx = 41 # try changing this number from 41 to 81 and Run 411 what happens? dx = 2 / (nx-1) nt = 25 #nt is the number of timesteps we want to calculate dt = .825 #dt is the amount of time each timestep covers (delta t) C = 1 u = numpy.ones (nx) #numpy function ones() u[int(.5 / dx): int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s print(u) un = numpy.ones(nx) #initialize a temporary array for n in range(nt): #loop for values of n from 0 to nt, so it will run nt times un = u.copy() print(un)##copy the existing values of u into un for i in range(1, nx): ## you can try commenting this line and... #for i in range(nx): ## ... uncommenting this line and see what happens! u[i] = un[i] - c + dt | dx (un[i] - un[i-1]) #print(u[i]) plt.plot(numpy.linspace(0, 2, nx), u); plt.show() The 1-D Linear Convection equation is the simplest, most basic model that can be used to learn something about CFD. It is surprising that this little equation can teach us so much! Here it is: da + c ot = 0 With given initial conditions (understood as a wave), the equation represents the propagation of that initial wave with speed c, without change of shape. Let the initial condition be u(x, 0) = ug(x). Then the exact solution of the equation is u(x, t) = u((x ct). We discretize this equation in both space and time, using the Forward Difference scheme for the time derivative and the Backward Difference scheme for the space derivative. Consider discretizing the spatial coordinate x into points that we index from i = 0 to N, and stepping in discrete time intervals of size At. From the definition of a derivative (and simply removing the limit), we know that: u(x) u(x + 4x) x Our discrete equation, then, is: in + 1 u u - u? to = 0 At x Where n and n + 1 are two consecutive steps in time, while i 1 and are two neighboring points of the discretized x coordinate. If there are given initial conditions, then the only unknown in this discretization is u? + 1. We can solve for our unknown to get an equation that allows us to advance in time, as follows: u" + 1 = c) = u? CA (u" " - 1) import numpy import matplotlib.pyplot as plt import time, sys nx = 41 # try changing this number from 41 to 81 and Run 411 what happens? dx = 2 / (nx-1) nt = 25 #nt is the number of timesteps we want to calculate dt = .825 #dt is the amount of time each timestep covers (delta t) C = 1 u = numpy.ones (nx) #numpy function ones() u[int(.5 / dx): int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s print(u) un = numpy.ones(nx) #initialize a temporary array for n in range(nt): #loop for values of n from 0 to nt, so it will run nt times un = u.copy() print(un)##copy the existing values of u into un for i in range(1, nx): ## you can try commenting this line and... #for i in range(nx): ## ... uncommenting this line and see what happens! u[i] = un[i] - c + dt | dx (un[i] - un[i-1]) #print(u[i]) plt.plot(numpy.linspace(0, 2, nx), u); plt.show()








