C Programming

You are the newly appointed captain of the HMS Knot Lost, and you need to help your crew back to land. Using your superior astronomy skills you have determined where you are in the ocean with respect to land. As we all know the shore line you are looking to reach can be modeled using parabola in the 2D plane. You know the function that models the parabola and the x y location of the ship currently. Your crew is tired and hungry, so you need to determine the smallest distance needed to travel to reach any part of the shore line. You decided that the program you will make will be able to help many ship quickly in the event of a complete fleet catastrophe.

Input Specification

The input will begin with an integer q (q 100,000), number of shore/ship pairs. The next q lines will each contain 5 space separated integers, a, b, c, x, and y (1 a 10,000; -10,000 b, c, x₀, y₀ 10,000), representing a different ship scenario. The ship is located at the point (x₀, y₀). The shoreline will be modeled by the parabola f(x) = ax²+bx+c. You are guaranteed that the y₀ ax₀²+bx₀+c.

Output Specification

For each shore/ship pair output the closest distance between the ship and the shore. You do not need to specify the exact point. Answers with at most 0.000001 absolute or relative error will be treated as correct.

For example if the correct answer is 1 billion, then answers between 1,000,001,000 and 999,999,000 inclusive, would be accepted.

Input Output Example

Input	Output
1 1 -4 3 8 2	4.12310562562
3 1 1 1 0 -2 1 0 -1 4 1 4 -10 25 10 10	2.78820252986 2.45853984495 12.3308676174

Explanation Case 1

The ship is at the point (8,2) and the parabola shore is the equation (1)*x²+(-4)*x+(3)

The closest point is at (4, 3). The distance of which is sqrt(4*4 + 1*1) = sqrt(17) which is approximately 4.1231056562.

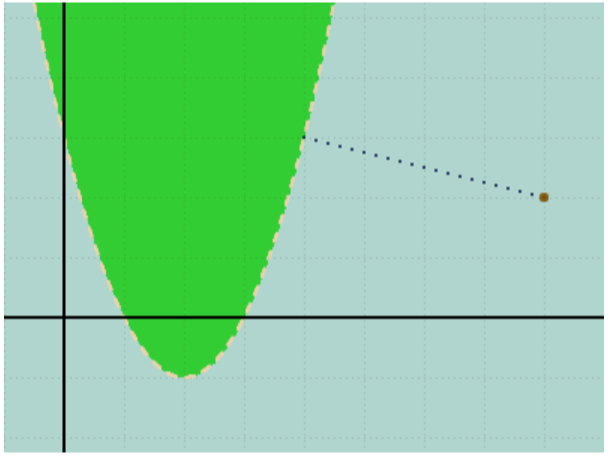
Note the parabola above is x²-4x+3

Case 2

The parabola is x²+x+1

For the first scenario the closest point on the parabola is at approximately (-0.42321621055638575 0.7558957503213213)

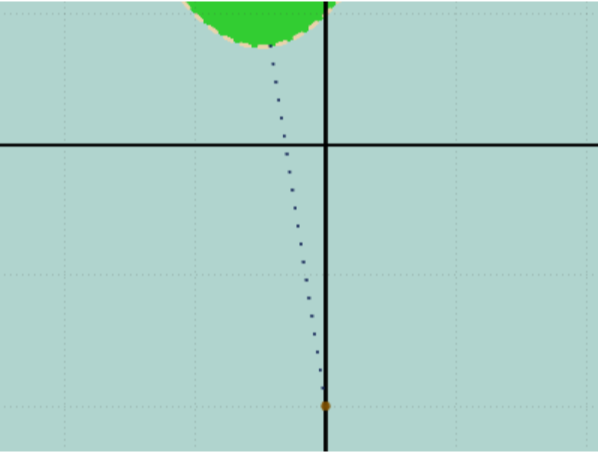
The parabola is x²-1

For the second scenario the closest point on the parabola is at approximately (1.647426664594562, 1.714014615217164)

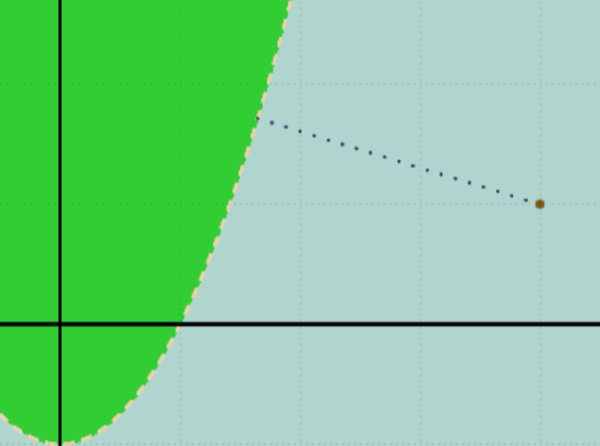
The parabola is 4x²-10x+25

For the final scenario of the second case the landing point is at approximately (1.3724127232591357, 18.80993949926287)

Advice

Solve the problem of the shortest distance by trying points on the parabola. Different points the on the parabola will have different distances to the ships location. Compute the distances based on these points and search for the optimum point using the ternary search.

Requirements

Has a function for finding the distance to the parabola based on a given x value

Searches until the range of the search area is small enough for an accurate answer

Your program will be tested on 10 test cases

You must use a logarithmic search

Transcribed image text