C++

You will practice writing and timing iterative and recursive versions of the same function. You will use the following code to time both versions of your solution to the Fibonacci problem described below.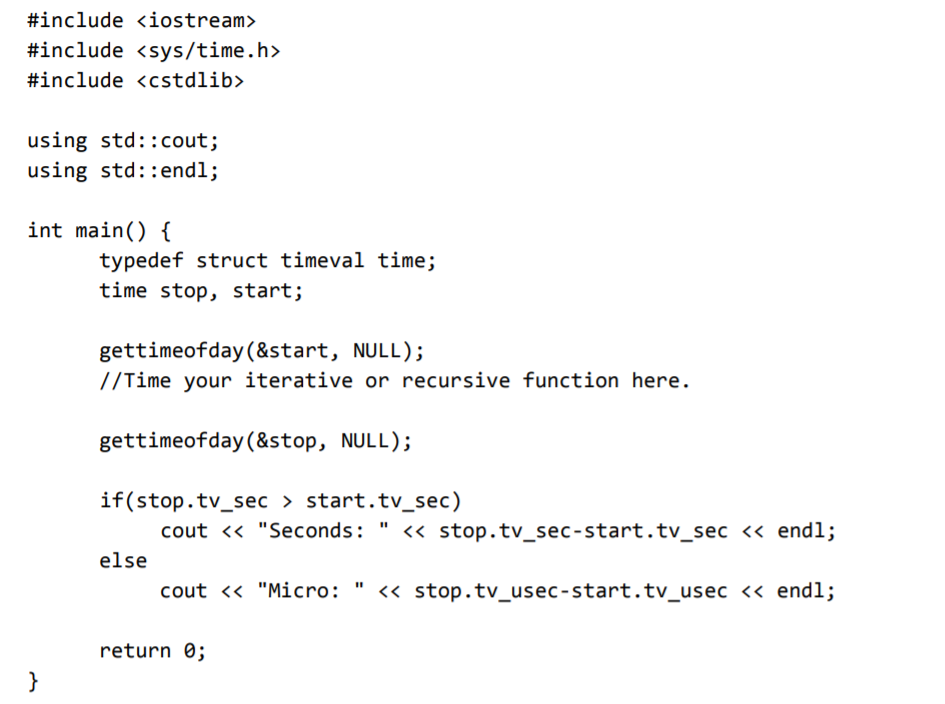First, you will write a function called, fib_iter(), that has one parameter, n, of type int, and returns the nth Fibonacci number, Fn . The Fibonacci numbers start with F0 is 0, F1 is 1, F2 is 1, F3 is 2, F4 is 3, F5 is 5, F6 is 8, etc... Formally stated: Fi+2 = Fi + Fi+1 for i = 2, 3, ; where F0 = 0 and F1 = 1 Your iterative version of the function should use a loop to compute each Fibonacci number, discarding numbers along the way, until you reach your desired number. Next, you will write a recursive version of the function called, fib_recurs(), that also takes one parameter, n, of type int, and returns the nth Fibonacci number, Fn . Using the code supplied above, time the iterative and recursive solutions for finding the 1 st , 5 th , 15 th , 25 th , and 45 th Fibonacci numbers. Determine how long each function takes, and compare and comment on your results. Show a trace through the recursive solution for n=5. Additionally, produce a table of times for n = 1, 5, 15, 25, and 45 for each version of the function.

#include #include #include iostream sys/time.h stdlib> using std::cout; using std: :endl; int main) typedef struct timeval time; time stop, start; gettimeofday (&start, NULL); //Time your iterative or recursive function here. gettimeofday (&stop, NULL); if(stop.tv_sec start.tv_sec) else cout