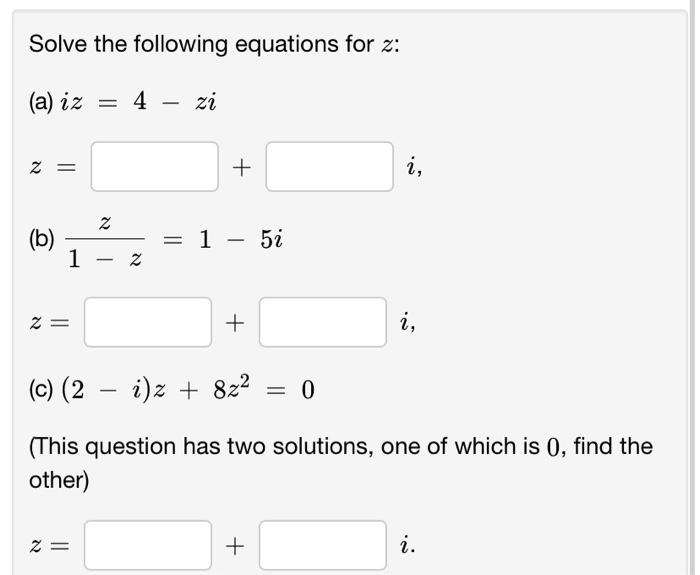
Calculate (2+i)+(3+3i) = (2+i) (3+3i) = - (2+ i)(3+3i) = The complex conjugate of (1 + i) is (1 - i). In general to obtain the complex conjugate reverse the sign of the imaginary part. (Geometrically this corresponds to finding the "mirror image" point in the complex plane by reflecting through the x-axis. The complex conjugate of a complex number z is written with a bar over it: and read as "z bar". Notice that if z = a + ib, then (2)(2)= |=a+62 which is also the square of the distance of the point z from the origin. (Plot z as a point in the "complex" plane in order to see this.) If =2+i then z = and |z|= You can use this to simplify complex fractions. Multiply the numerator and denominator by the complex conjugate of the denominator to make the denominator real. 2+i 3+3i +i Two convenient functions to know about pick out the real and imaginary parts of a complex number. Re(a+ib) a (the real part (coordinate) of the complex number), and Im(a+ib) = b (the imaginary part (coordinate) of the complex number. Re and I'm are linear functions -- now that you know about linear behavior you may start noticing it often 8 Find all solutions of the equation x + 3+ = 0 and give x your answer as a list of complex numbers, such as 3-4i, 5+i. Place the following in order: (a) z1+%2 (b)|12-11 (c) 21 22 (d) 22-21 Answer: VI VI VI Calculate: (a) - 4+2 -1 - 4i = (b) | (1 + i)(3 2i)(4 4i)| i(4 + 4i) (c) = (1 - 3i) (d) ( + i) 100 (T - 2) 100/ = = Solve the following equations for z: (a) iz = 4 - zi z = (b) 1 x = 2 - + i, Z = 1 - 5i + i, i)z + 8z = 0 (c) (2 - i)z + (This question has two solutions, one of which is 0, find the other) x = + i.