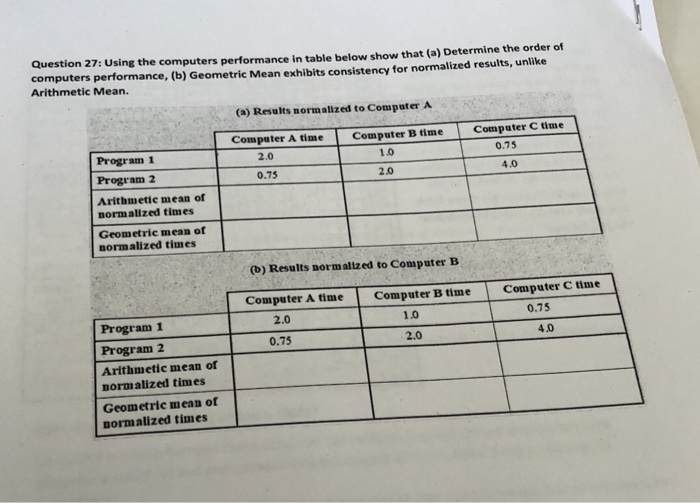
Calculate the arithmetic mean below ...
For the ODE 2 dy + 3xy = e-1.5x dx y(0) = 3, estimate y(4) with a step size of 2 using a. Heun's Runge-Kutta 2nd order method b. Midpoint Runge-Kutta 2nd order method c. Ralston's Runge-Kutta 2nd order methodDetermine whether the value is a discrete random variable, continuous random variable, or not a random variable a. The time it takes for a light bulb to burn out by The number of light bulbs that burn out in the next week in a room with 12 bulbs c. The political party afdation of adults in the United States d. The number of free throw attempts before the first shot is made e. The number of textbook authors now sitting at a computer I. The square footage of a house al la the time it takes for a light bulb to burn out a discrete random variable, a continuous random variable, or not a random variable? O A. Ills a discrete random variable. O B. It is a continuous random variable O C. it is not's random variable b. is the number of light bulbs that burn out in the next week in a room with 12 bulbs a discrete ran continuous random variably, or not a random variable? O A Is a discrete fandom variable Of. lba continuous random variable C. Iis not a random variable c. Is the political party allisation of adults in the United States a discrete random variable, a continuous random variable, or not a random variable? A. Bis a continuous random variable O.B. It is a discrete random variable. O C. itis not a random variable d. Is the number of free-throw attempts before the first shot is made a discrete random variable, a continuous random variable, or not a random variable? O A it is a continuous random variable Q B: i is a discrete random variable C his not a random veilable orla the number of textbook authors now siting at a computer a discrete random want continuous random variable, or not a random variable? @ A. is a decrole random vailabio OH, It is a continuous random variable OC. libs bot avidavailable Cher to select your answerDetermine whether the value is a discrete random variable, continuous random variable, or not a random variable. a. The height of a randomly selected giraffe b. The number of points scored during a basketball game c. The political party affiliation of adults in the United States d. The number of people with blood type A in a random sample of 14 people e. The number of free-throw attempts before the first shot is made f. The number of light bulbs that burn out in the next week in a room with 17 bulbs a. Is the height of a randomly selected giraffe a discrete random variable, a continuous random variable, or not a random variable? O A. It is a discrete random variable. O B. It is a continuous random variable. O C. It is not a random variable. b. Is the number of points scored during a basketball game a discrete random variable, a continuous random variable, or not a random variable? O A. It is a continuous random variable. O B. It is a discrete random variable. O C. It is not a random variable c. Is the political party affiliation of adults in the United States a discrete random variable, a continuous random variable, or not a random variable? O A. It is a continuous random variable. O B. It is a discrete random variable. O C. It is not a random variable. d. Is the number of people with blood type A in a random sample of 14 people a discrete random variable, a continuous random variable, or not a random variable? O A. It is a discrete random variable. O B. It is a continuous random variable. O C. It is not a random variable.Question 27: Using the computers performance in table below show that (a) Determine the order of computers performance, (b) Geometric Mean exhibits consistency for normalized results, unlike Arithmetic Mean. (a) Results normalized to Computer A Computer A time Computer B time Computer C time Program 1 2.0 1.0 0.75 Program 2 0.75 2.0 4.0 Arithmetic mean of normalized times Geometric mean of normalized times (b) Results normalized to Computer B Computer A time Computer B time Computer C time Program 1 2.0 1.0 0.75 Program 2 0.75 2.0 4.0 Arithmetic mean of normalized times Geometric mean of normalized times