Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Calculate the following: (a) Compute the eigenvalues ( lambda_{1} ) and ( lambda_{2} ) of ( R ) and the corresponding eigenvectors ( gamma 1
Calculate the following: (a) Compute the eigenvalues ( lambda_{1} ) and ( lambda_{2} ) of ( R ) and the corresponding eigenvectors ( gamma 1 ) and ( gamma_{2} ) of ( R ) : [ R=left[egin{array}{cc} 0.9 & 1 \ 1 & 0.9 end{array} ight] ] (b) Show that ( lambda_{1}+lambda_{2}=operatorname{tr}(R) ) where the trace of a matrix equals the sum of its diagonal components. (c) Show that ( lambda_{1} imes lambda_{2}=I R I ) where ( I R I ) is the determinant of the matrix.
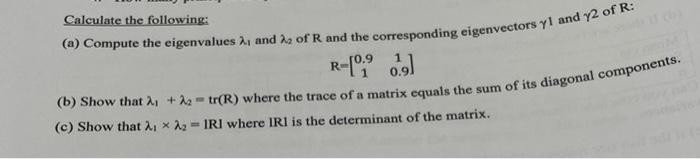
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


