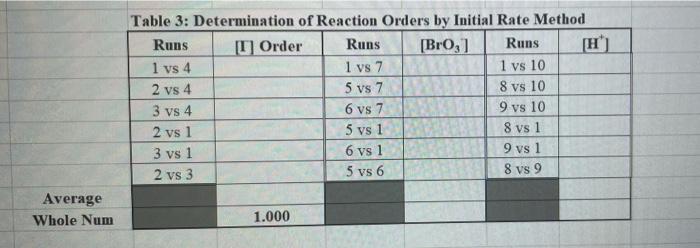
1. Calculate the order of BrO₃, I and H⁺using as many comparative runs as.

   For [I] use comparisons for runs 1:4, 2:4, 3:4, 2:1, 3:1, 2:3

   For [BrO₃] use comparisons for runs 1:7, 5:7, 6:7, 5:1, 6:1, 5:6

   For [H⁺] use comparisons for runs 1:10, 8:10, 9:10, 8:1, 9:1, 8:9

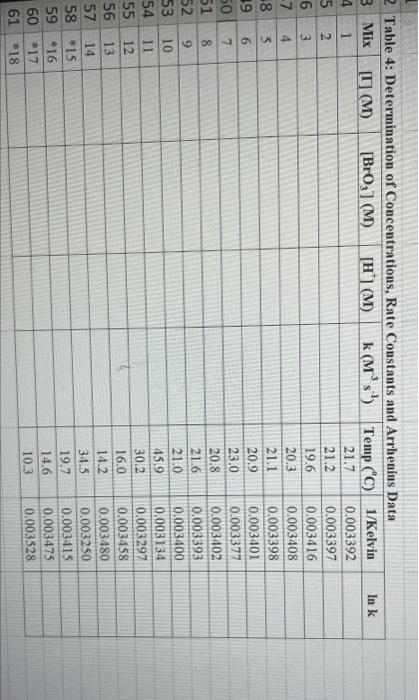
2. Calculate the rate constant (k) for all runs at room temperature and determine the average k.
3. Calculate k at the different temperatures for the uncatalyzed runs using #11-14 and for the catalyzed runs using #15-18.

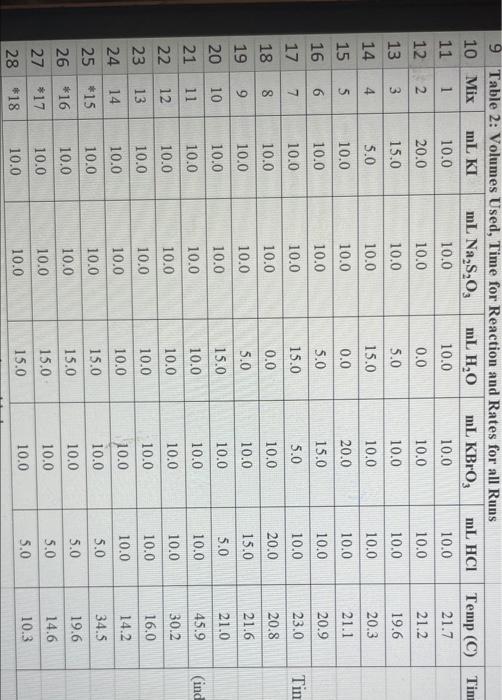
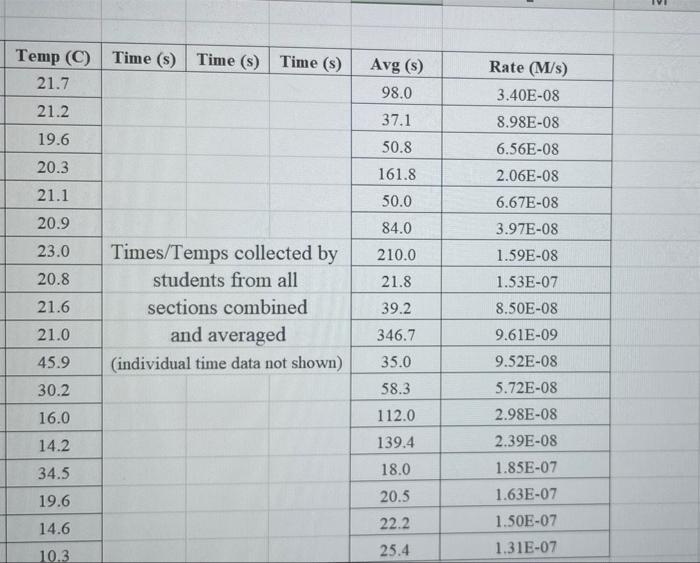
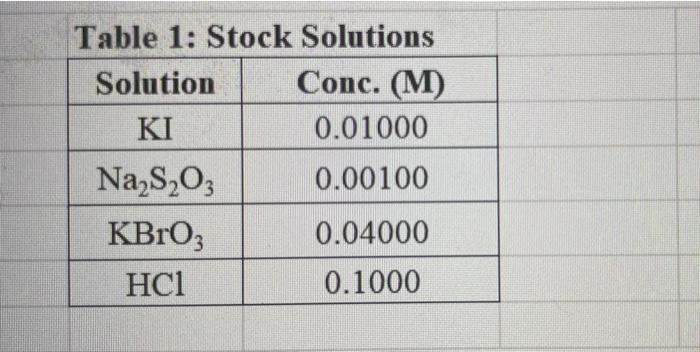
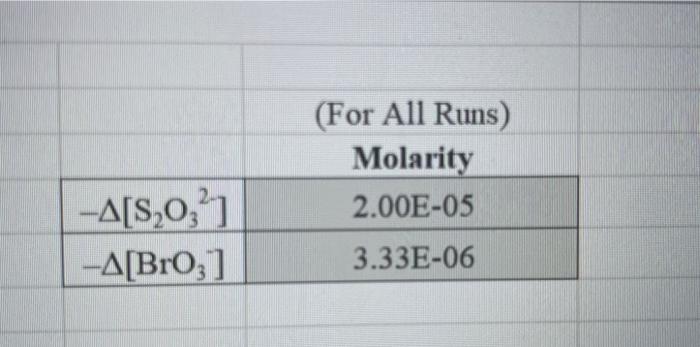
INTRODUCTION: This experiment involves the study of the rate properties, or chemical kinetics, of the following reaction between iodide ion and bromate ion under acidic conditions: 6 1(aq) + BrO3-(aq) + 6H* (aq) 3 12(aq) + Br(aq) + 3 H2O() This reaction proceeds reasonably slowly at room temperature, its rate depending on the concentrations of the I-, BrO3-, and Hions according to the rate law. For this reaction the rate law takes the form: Rate = k [14] [BrO;-)" [H]P One of the main objectives of the experiment is to evaluate the rate constant k and the reaction orders m, n, and p for this reaction. We will also investigate the manner in which the reaction rate depends on temperature and will determine the activation energy, Es for the reaction. The reaction rate is determined by measuring the time between mixing the reactants and the appearance of the Iz product which forms a deep blue color with starch that is added to act as an indicator. The reaction is reasonably slow, but still too fast to be measured directly. Therefore, a constant amount of another substance (the clock) is added. This substance, the thiosulfate ion (S2032 reacts with the 12 as it is formed. There is no 12 to react with the starch until after all the S2032-ions are used up, at which time the solution turns dark blue. I2 + 2 S20,2- 21 + S4062- By carrying out the main reaction in the presence of S2032- and a starch indicator, we introduce a "clock" into the system. Our clock tells us when a given amount of Broy-ion has reacted (1 mole BrOs per 6 moles Sz032), which is just what we need to know, since the rate of reaction can be expressed in terms of the time it takes for a particular amount of BrO3- to be used up. In all our reactions, the amount of BrO;- that reacts in the time we measure is constant, since the S203 - is the limiting reagent and small when compared to the amounts of the other reactants. This means that the concentrations of all other reactants is effectively constant during the timing. A(3,01 --A[Broj] Rate = At Since the A[BrO3-) is based on ALL the thiosulfate reacting, it is constant for all runs. The rate can Absolute Rate A[B:03) or Relative Rate - Constant At At therefore be expressed as the inverse of the time. We actually use any convenient value for the constant and refer to the relative rate. In either case, when we compare two rates we get: constant 11 3 Ratel Rate 2 constant t1 The reaction order with respect to each reactant is determined by comparing runs where the concentrations of two reactants remain constant and the third is changed (for example--cut in half) as shown in the table below. [BrO;" [1] Time [H') A Run 1 B . ti Run 2 B 12 A: A: C C Run 3 B2 ty Run 4 , B C2 t4 Notice that when two runs are compared only one concentration at a time is varied so that the dependence of that component can be determined. For Run I: Rate; = k [C] [B]" [A1]P For Run 2: Rate = k [C]" [B]" [A2]P rate log rate 2 P log A A The runs similarly establish n and m and k can be calculated from any one of the runs. In the first part of this experiment the concentrations of BrO3-, 1-. and Hare systematically changed and each solution is mixed in the presence of a constant small amount of S:03. The time it takes for each reaction mixture to turn blue is measured. In the second part of the experiment the dependency of the reaction rate upon the temperature is investigated while concentration is held constant. In general, a reaction rate increases sharply with temperature. By measuring the variance of the rate constant with temperature, we can determine the activation energy. Ea, by making use of the Arrhenius equation: -E. k - Ae or Ink A + In A R Temp (C) Tin 21.7 21.2 19.6 20.3 21.1 20.9 23.0 20.8 Tin 9 Table 2: Volumes Used, Time for Reaction and Rates for all Runs 10 Mix mL KI mL Na,s,o, mL HO mL KBrO; mL HCI 11 1 10.0 10.0 10.0 10.0 10.0 12 2 20.0 10.0 0.0 10.0 10.0 13 3 15.0 10.0 5.0 10.0 10.0 14 4 5.0 10.0 15.0 10.0 10.0 15 5 10.0 10.0 0.0 20.0 10.0 16 6 10.0 10.0 5.0 15.0 10.0 17 7 10.0 10.0 15.0 5.0 10.0 18 8 10.0 10.0 0.0 10.0 20.0 19 9 10.0 10.0 5.0 10.0 15.0 20 10 10.0 10.0 15.0 10.0 5.0 21 11 10.0 10.0 10.0 10.0 10.0 12 22 10.0 10.0 10.0 10.0 10.0 13 23 10.0 10.0 10.0 10.0 10.0 14 24 10.0 10.0 10.0 10.0 10.0 25 *15 10.0 10.0 10.0 15.0 5.0 10.0 10.0 26 *16 5.0 10.0 15.0 27 *17 10.0 10.0 5.0 15.0 10.0 *18 28 5.0 10.0 10.0 10.0 15.0 21.6 21.0 (ind 45.9 30.2 16.0 14.2 34.5 19.6 14.6 10.3 Temp (C) Time (s) Time (s) Time (s) 21.7 Avg (s) 98.0 37.1 21.2 Rate (M/s) 3.40E-08 8.98E-08 6.56E-08 2.06E-08 19.6 50.8 20.3 161.8 21.1 6.67E-08 20.9 23.0 50.0 84.0 210.0 21.8 39.2 346.7 20.8 Times/Temps collected by students from all sections combined and averaged (individual time data not shown) 21.6 21.0 3.97E-08 1.59E-08 1.53E-07 8.50E-08 9.61E-09 9.52E-08 5.72E-08 2.98E-08 2.39E-08 1.85E-07 45.9 35.0 58.3 30.2 16.0 112.0 14.2 139.4 34.5 19.6 18.0 20.5 22.2 14.6 1.63E-07 1.50E-07 1.31E-07 10.3 25.4 Table 3: Determination of Reaction Orders by Initial Rate Method Runs [T] Order Runs [Br03] Runs 1 vs 4 1 vs 7 1 vs 10 2 vs 4 5 vs 7 8 vs 10 3 vs 4 6 vs 7 9 vs 10 2 vs 1 5 vs 1 8 vs 1 3 vs 1 6 vs 1 9 vs 1 2 vs 3 5 vs 6 8 vs 9 Average Whole Num 1.000 In k 2 Table 4: Determination of Concentrations, Rate Constants and Arrhenius Data 3 Mix D] (M) [Br0, (M) [H](M) k( ms) Temp (C) 1/Kelvin 4 1 21.7 0.003392 5 2 21.2 0.003397 6 3 19.6 0.003416 -7 4 20.3 0.003408 8 21.1 0.003398 19 6 20.9 0.003401 50 7 23.0 0.003377 51 20.8 0.003402 52 9 21.6 0.003393 53 10 21.0 0.003400 54 11 45.9 0.003134 55 12 30.2 0.003297 56 16.0 0.003458 13 14.2 57 14 0.003480 58 34.5 0.003250 *15 19.7 0.003415 59 *16 14.6 0.003475 60 *17 10.3 0.003528 61 *18 S000 Table 1: Stock Solutions Solution Conc. (M) KI 0.01000 Na S203 0.00100 KBrO; 0.04000 HC1 0.1000 (For All Runs) Molarity 2.00E-05 -A[S,0,?] -A[BrO;] 3.33E-06