Calculus 2

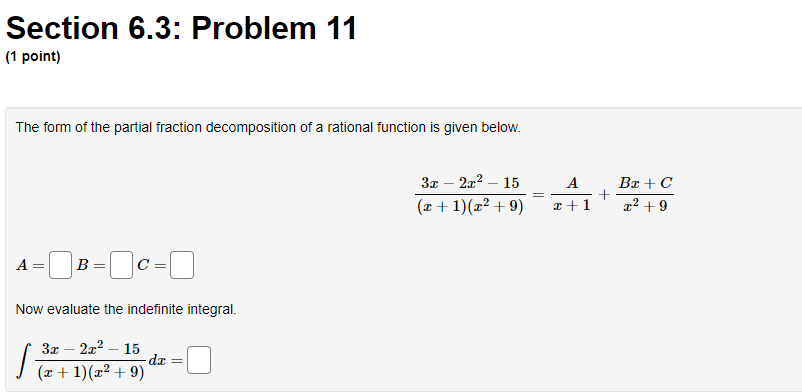
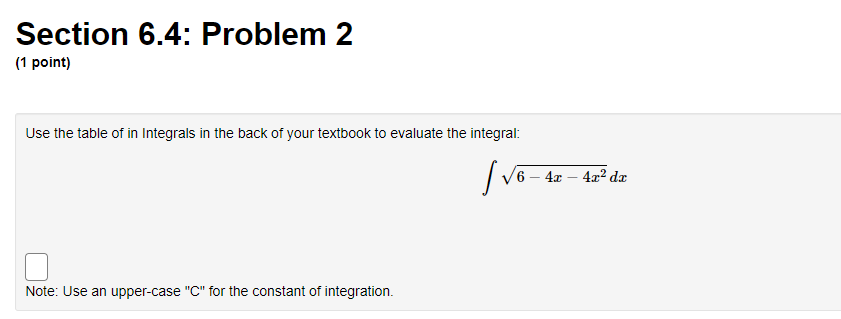
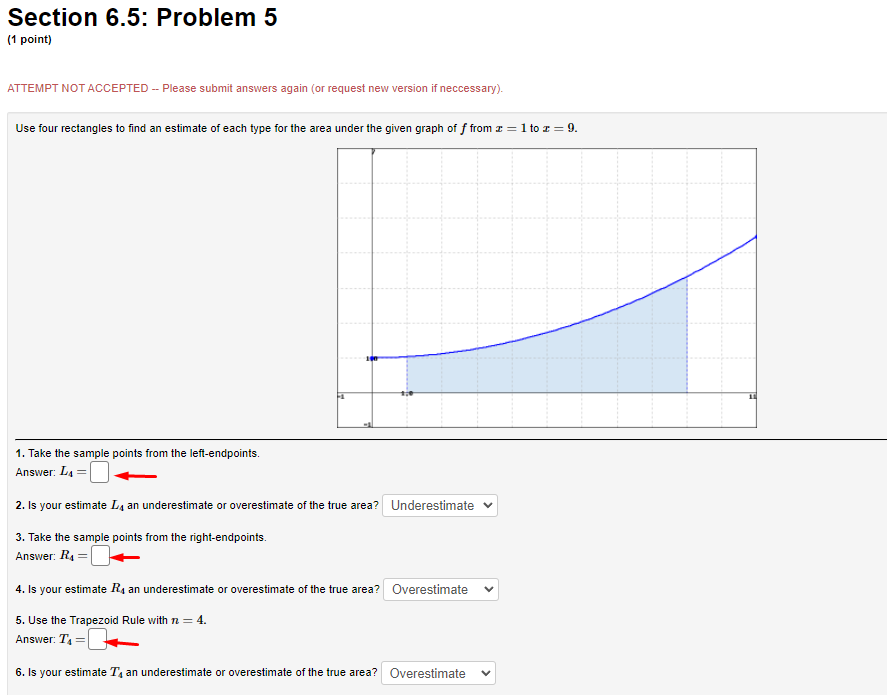
Section 6.3: Problem 11 (1 point) The form of the partial fraction decomposition of a rational function is given below. 3x - 2x- - 15 A Ba + C (x + 1)(x2 +9) T2 +9 A Now evaluate the indefinite integral. 3x - 2x2 - 15 - = (x + 1) (x2 +9)Section 6.4: Problem 2 [1 paint) Use the table of in Integrals in the hack of your textbook to evaluate the integral: f 64243211'2: D Note: USE an UPPEI-CESE "C" for the constant ofintegration. Section 6.3: Problem 3 (1 point) Note: You can get full credit for this problem by just entering the final answer (to the last question) correctly. The initial questions are meant as hints towards the final answer and also allow you the opportunity to get partial credit. Consider the indefinite integral (x - 4)(x - 5)2 dx Then the integrand has partial fractions decomposition C + 4 5 (x - 5)2 where h= C= Integrating term by term, we obtain that do = (x - 4) (x - 5)2 +CSection 6.4: Problem 5 (1 point) Use the Table of Integrals to evaluate the integral. 1 ,23 - 1 da =Section 6.5: Problem 5 (1 point) ATTEMPT NOT ACCEPTED -- Please submit answers again (or request new version if necessary). Use four rectangles to find an estimate of each type for the area under the given graph of f from = = 1 to r = 9. 1. Take the sample points from the left-endpoints. Answer: LA = 2. Is your estimate 4 an underestimate or overestimate of the true area? Underestimate v 3. Take the sample points from the right-endpoints. Answer: R4 = 4. Is your estimate Is an underestimate or overestimate of the true area? |Overestimate 5. Use the Trapezoid Rule with n = 4. Answer: Ti = 6. Is your estimate 74 an underestimate or overestimate of the true area? |OverestimateSection 6.4: Problem 6 (1 point) Use the reduction formula (In(z))" de = z(In(z))" - n /(In(z))" lax to evaluate the integral (In(z) )3 dx. Note: Use an upper-case "C" for the constant of integration