Calculus 3 :

final answer only please

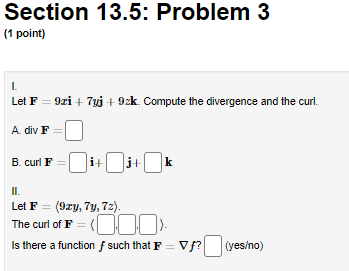
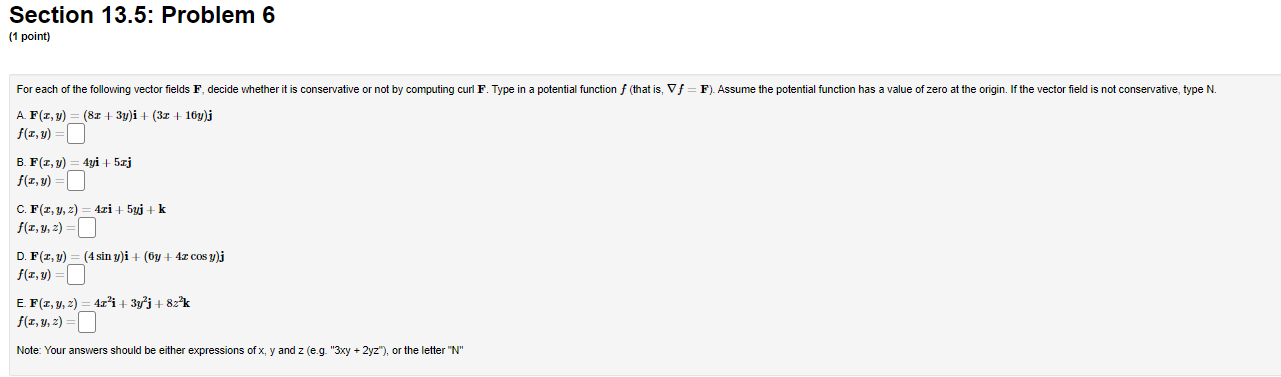
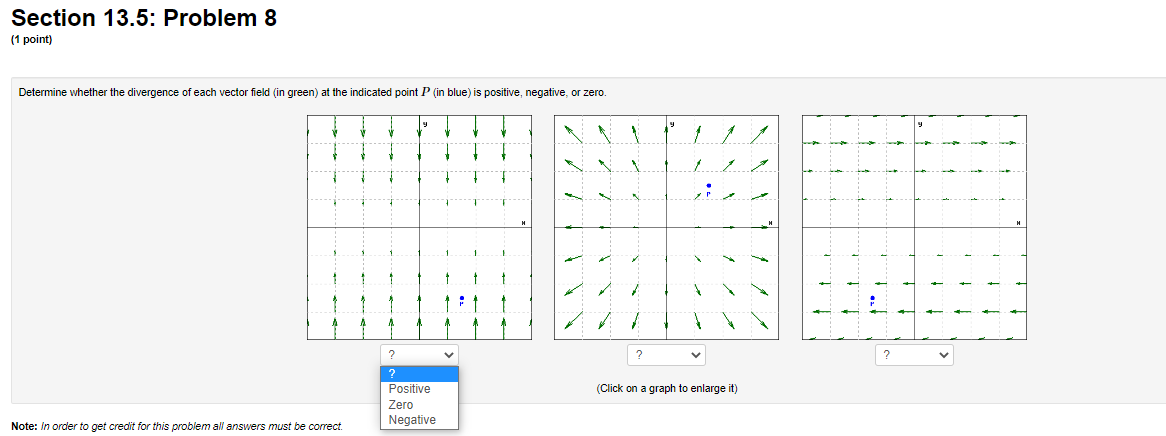
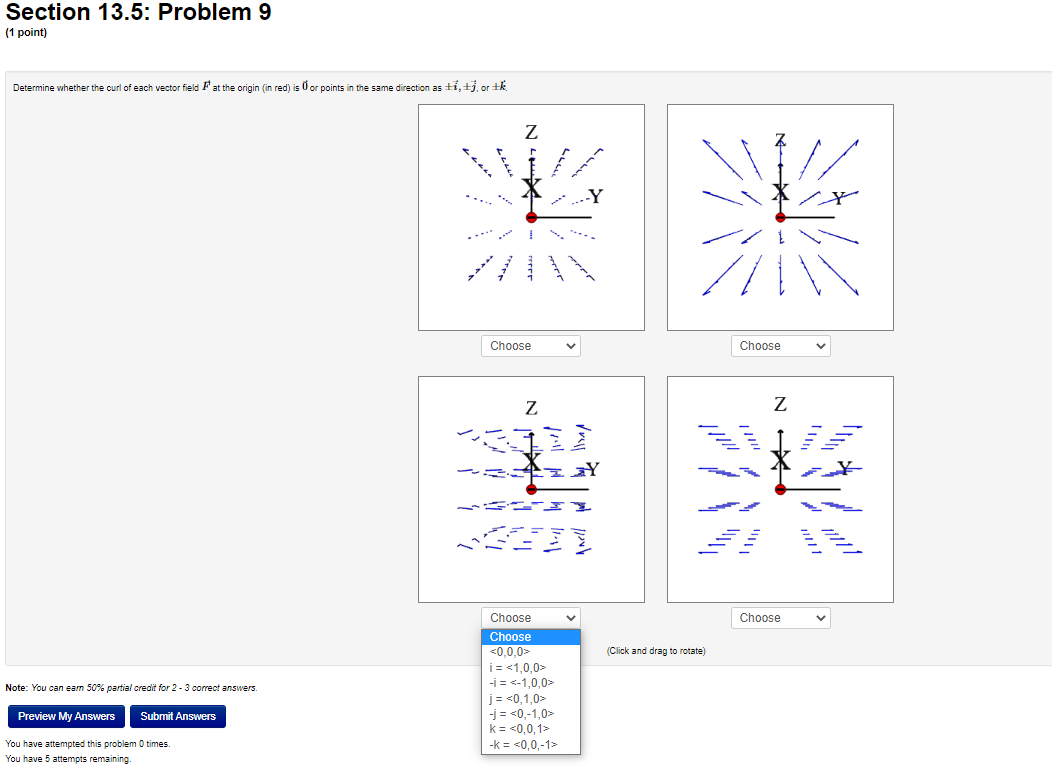
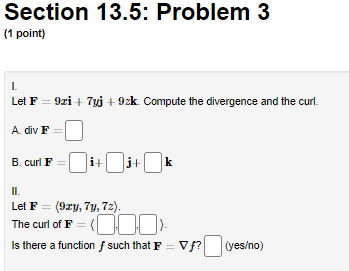
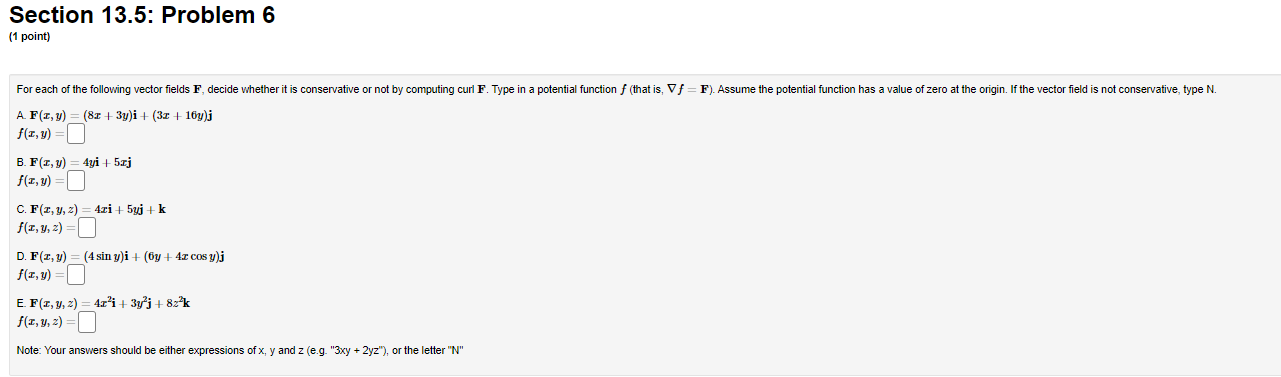
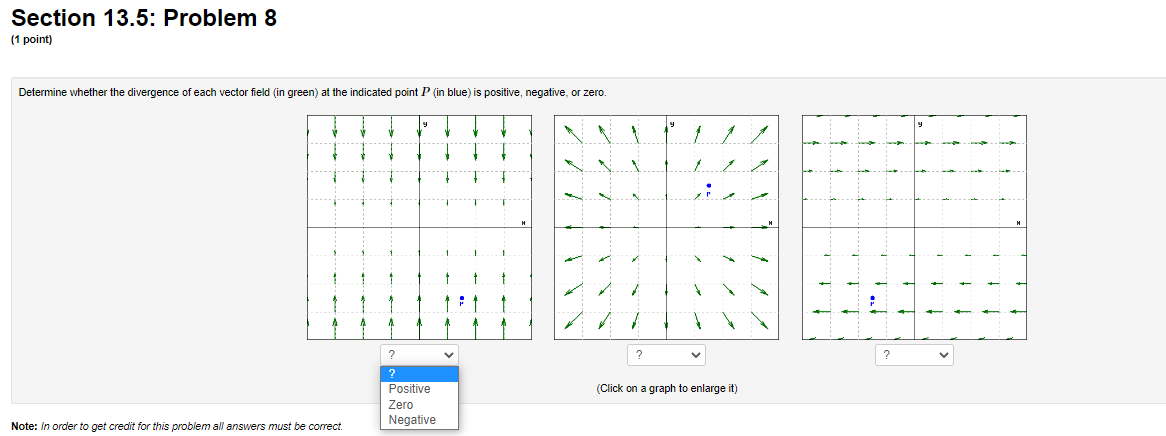
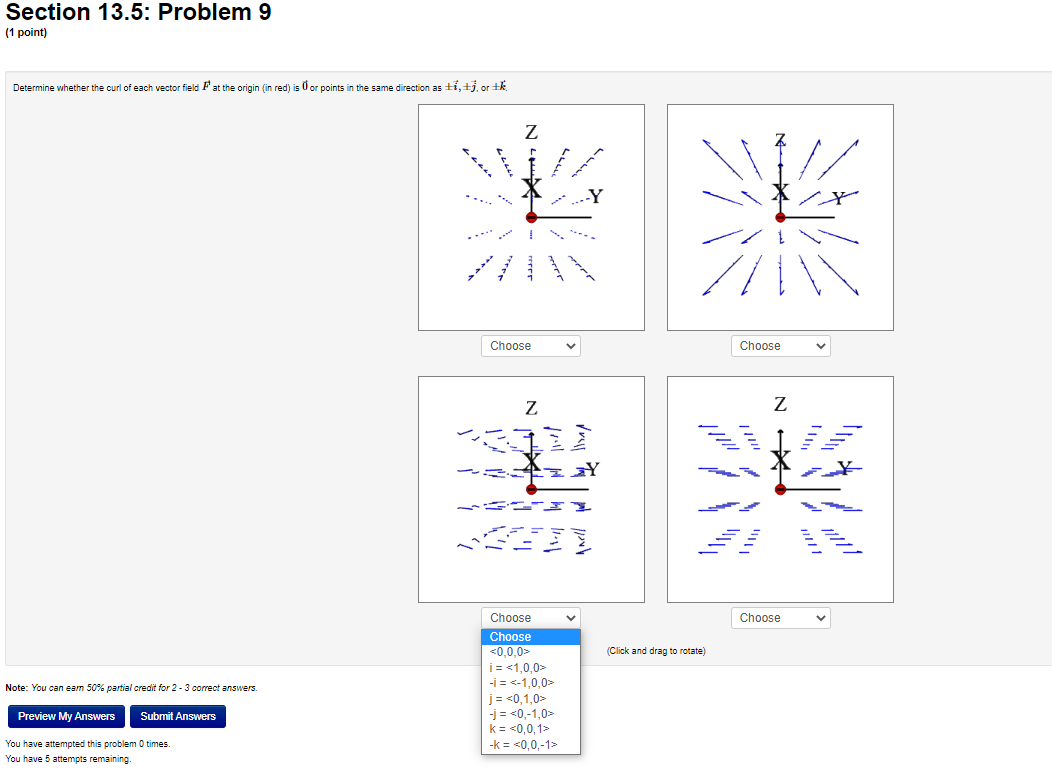
Section 13.5: Problem 1 (1 point) Show that the vector field F(I, y, 2) = (by cos(8x), 8x sin(by), 0) is not a gradient vector field by computing its curl. How does this show what you intended? curl(F) = V xF=(00>Section 13.5: Problem 2 (1 point) A) Consider the vector field F(I, 1, 2) = (7yz, -612, 7ry). Find the divergence and curl of F. div (F) = V . F= curl (F) = V x F = B) Consider the vector field F(I, #, 2) = (-I,3(x + y) , -3(x + y+2)?). Find the divergence and curl of F. div (F) = V . F= curl (F) = V x F =Section 13.5: Problem 3 (1 point) Let F = 9xi + 7yj + Ock. Compute the divergence and the curl. A div F B. curl F i- 1- k II. Let F = (9ry, 7y, 72). The curl of F Is there a function f such that F = V /? (yeso)Section 13.5: Problem 4 (1 point) Consider the vector field F(I, y, 2) = (9y, 91, 52). Show that F is a gradient vector field F = VV by determining the function V which satisfies V(0, 0, 0) = 0. V(I, y, =)=Section 13.5: Problem 5 (1 point] Let F = (4ruz | 8 sin x, 2x 2, 2x y). Find a function f so that F = V f, and f(0, 0, 0) = 0.Section 13.5: Problem 6 (1 point) For each of the following vector fields F, decide whether it is conservative or not by computing curl F. Type in a potential function f (that is, V f = F). Assume the potential function has a value of zero at the origin. If the vector field is not conservative, type N. A F(z, y) = (81 + 3y)i + (32 + 16y)j f(I, y) =] B. F(x, y) = 4yi + 5xj f(I, y) =] C. F(I, y, z) = 4ri + 5gj + k f(I, y, =) = D. F(z, y) = (4sin y)i + (by + 4x cosy)j f(I, y) = E F(r, y, 2) = 4r i + 3y j + 82 k f(I, y, =) = Note: Your answers should be either expressions of x, y and z (e.g. "3xy + 2yz"), or the letter "N"Section 13.5: Problem 7 (1 point) Let F be any nonconstant vector field of the form F = f(x)i + g(y)j + h(z)k and let G be any nonconservative vector field of the form G = f(y, z)i + g(z, 2)j + h(I, )k. Indicate whether the following statements are true or false by placing "T" or "F" to the left of the statement. 1. G is irrotational 2. F is irrotational 3. F is incompressible 4. G is incompressibleSection 13.5: Problem 8 (1 point) Determine whether the divergence of each vector field (in green) at the indicated point P (in blue) is positive, negative, or zero. y ? ? Positive (Click on a graph to enlarge it) Zero Note: In order to get credit for this problem all answers must be correct. NegativeSection 13.5: Problem 9 (1 point) Determine whether the curl of each vector field F at the origin (in red) is 0 or points in the same direction as ti, +7, or #. N Choose Choose v Z Z X Choose Choose v Choose (Click and drag to rotate) i= Note: You can eam 50%% partial credit for 2 - 3 correct answers. -i = j = Preview My Answers ubmit Answers -j = k = You have attempted this problem 0 times. -k = You have 5 attempts remaining