Calculus 3 Sections 12.1 and 12.2 Reading Assignment: 3D Coordinates and Vectors

Answer Only Exercise 1 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very carefully and see on what it is asking for and what is really about. Please be very serious careful with this assignment of exercise #1.

References: Thomas' Calculus: Early Transcendentals | Calculus | Calculus | Mathematics | Store | Pearson+

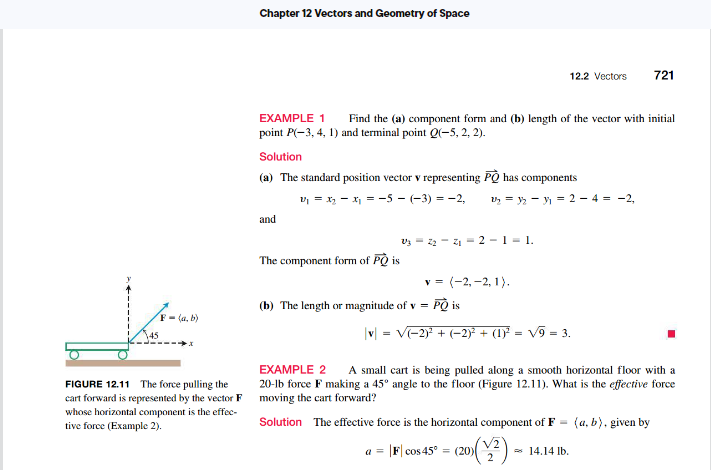
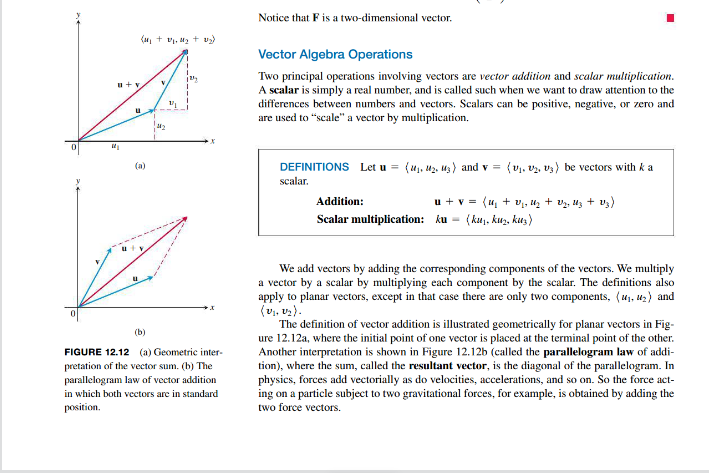
Sections 12.1 and 12.2 Reading Assignment: 3D Coordinates and Vectors Instructions. Read through this assignment and complete the three exercises below by reading the appropriate passages of the textbook. Before we can get into calculus, we need to discuss three-dimensional space and its geometry. The coordinate system in 3D works like the 2D version, but there is an idea of orientation and the right-hand rule that is covered on p. 714. A useful variant of the right-hand rule is given by: (1) the index finger points in the x-direction, (2) the middle finger points in the y-direction, and (3) the thumb points in the z-direction. This helps with drawing coordinate systems and for the cross product (12.4). It is worth warning you that this only works with your right hand as the name suggests. Besides that, there are the formulas for distance (p. 716) and the equations of spheres (p. 716) that are similar to 2D distance and circles. We'll encounter a few spheres in this class and some distance computations. So it's important to keep these in mind, but hopefully these are similar enough to the 2D situation that it's not too much trouble to adapt to the 3D case. Next, we move on to vectors, which provide a helpful language to describe many multidimensional (both 2D and 3D) ideas. Ideally, you've seen them before, but if not, we cover here from the start. When writing vectors by hand, do not attempt to use bold font. Instead use arrows on top of the vector variable to indicate that it's a vector. For example, write v = (V1, V2, V3). It's also important to be consistent here. Other sources may use different notation, but for this class, it's important to use arrows for vectors and the angled brackets when writing in component form. A vector is visualized as an arrow and consists of a magnitude and a direction. When thinking about the meaning of a vector, it's best to consider both its magnitude and direction. Sometimes, the direction is more important. There are formulas for both magnitude (p. 720) and direction (p. 723).Exercise 1. Read Example 1(a) (p. 721). Explain how to find the component form of the vector PQ from the coordinates of the points P and Q. Example 2 (p. 721) points out an important example of a vector. Force (from physics) is a vector. Its magnitude represents the "strength" of the force, and its direction points to where the force is acting.Chapter 12 Vectors and Geometry of Space 12 Vectors and the Geometry of Space OVERVIEW In this chapter we begin the study of multivariable calculus. To apply calcu- lus in many real-world situations, we introduce three-dimensional coordinate systems and vectors. We establish coordinates in space by adding a third axis that measures distance above and below the xy-plane. Then we define vectors, which provide simple ways to define equations for lines, planes, curves, and surfaces in space.12.1 Three-Dimensional Coordinate Systems To locate a point in space, we use three mutually perpendicular coordinate axes, arranged as in Figure 12.1. The axes shown there make a right-handed coordinate frame. When you hold your right hand so that the fingers curl from the positive x-axis toward the positive y-axis, your thumb points along the positive z-axis. So when you look down on the xy- plane from the positive direction of the z-axis, positive angles in the plane are measured counterclockwise from the positive x-axis and around the positive z-axis. (In a left-handed coordinate frame, the z-axis would point downward in Figure 12.1 and angles in the plane would be positive when measured clockwise from the positive x-axis. Right-handed and left-handed coordinate frames are not equivalent.) The Cartesian coordinates (x, y, 2) of a point P in space are the values at which the planes through P perpendicular to the axes cut the axes. Cartesian coordinates for space are also called rectangular coordinates because the axes that define them meet at right angles. Points on the x-axis have y- and z-coordinates equal to zero. That is, they have coordinates of the form (x. 0. 0). Similarly, points on the y-axis have coordinates of the form (0, y. 0), and points on the z-axis have coordinates of the form (0, 0, z). The planes determined by the coordinates axes are the xy-plane, whose standard - constant equation is z = 0; the yz-plane, whose standard equation is x = 0; and the xz-plane, (0, 0, 2) whose standard equation is y = 0. They meet at the origin (0, 0, 0) (Figure 12.2). The (0. y, 2) origin is also identified by simply 0 or sometimes the letter O. The three coordinate planes x = 0, y = 0, and z = 0 divide space into eight cells (r, 0. z) called octants. The octant in which the point coordinates are all positive is called the first octant; there is no convention for numbering the other seven octants. The points in a plane perpendicular to the x-axis all have the same x-coordinate, this being (0. y. 0) the number at which that plane cuts the x-axis. The y- and z-coordinates can be any numbers. y (r, 0, 0) Similarly, the points in a plane perpendicular to the y-axis have a common y-coordinate and " = constant the points in a plane perpendicular to the z-axis have a common z-coordinate. To write equa- * = constant tions for these planes, we name the common coordinate's value. The plane x = 2 is the plane perpendicular to the x-axis at x = 2. The plane y = 3 is the plane perpendicular to the y-axis FIGURE 12.1 The Cartesian coordinate at y - 3. The plane z - 5 is the plane perpendicular to the z-axis at z - 5. Figure 12.3 system is right-handed. shows the planes x = 2, y = 3, and z = 5, together with their intersection point (2, 3, 5). 714Chapter 12 Vectors and Geometry of Space 716 Chapter 12 Vectors and the Geometry of Space Distance and Spheres in Space The formula for the distance between two points in the xy-plane extends to points in space. The Distance Between P(x], )'1, z ) and P,(X2. V2, Z2) | PRI = V( - n)+ ( - n) + (2 - 2) Proof We construct a rectangular box with faces parallel to the coordinate planes and the points , and A at opposite corners of the box (Figure 12.5). If A(ry, ), 2) and B(x2 32. z ) are the vertices of the box indicated in the figure, then the three box edges PA, AB, and BP, have lengths |PA = *2- x, AB = 12 - 3. BP) = |2 - 21. Because triangles A BP, and RAB are both right-angled, two applications of the Pythago rean theorem give and (see Figure 12.5). So FIGURE 12.5 We find the distance be- tween A and /2 by applying the Pythago rean theorem to the right triangles PAR = [A|2 + |AB|3 + |BP,|2 Substitute | PB|? = [MAP + JAB]]. and P BP. = x2 - x/3 + 32 - ml? + |2-z| =(1 - x)+ ( - >)'+(2 -a). Therefore EXAMPLE 3 The distance between P(2, 1. 5) and P(-2. 3, 0) is |RRI = V(-2 - 2) + (3 - 1) + (0 -5) = V16 + 4 + 25 = V45 = 6.708.We can use the distance formula to write equations for spheres in space (Figure 12.6). A point P(x, y, z) lies on the sphere of radius a centered at P(xg. ), 2) precisely when P(x. y. {) |PP) = a or (- x)+ (y- m)+ ( - z)' =a. The Standard Equation for the Sphere of Radius a and Center (X(, Jo. Zn) (x- 2)+(- >)+ (-z)'=a EXAMPLE 4 Find the center and radius of the sphere FIGURE 12.6 The sphere of radius a centered at the point ( )o Z, )- x+ y' + z+ 3 - 42+ 1=0. Solution We find the center and radius of a sphere the way we find the center and radius of a circle: Complete the squares on the x-, y-, and z-terms as necessary and write eachChapter 12 Vectors and Geometry of Space 720 Chapter 12 Vectors and the Geometry of Space (Xx 2. ya. 23) In textbooks, vectors are usually written in lowercase, boldface letters, for example u, v. and w. Sometimes we use uppercase boldface letters, such as F, to denote a force vector. In handwritten form, it is customary to draw small arrows above the letters, for example u, Position vector ("1. "2, 13) 1, w, and F. of Po We need a way to represent vectors algebraically so that we can be more precise about the direction of a vector. Let v = PO. There is one directed line segment equal to PO whose initial point is the origin (Figure 12.10). It is the representative of v in standard position and is the vector we normally use to represent v. We can specify v by writing the coordinates of its terminal point (vj, v2, v;) when v is in standard position. If v is a vector in the plane its terminal point (vj. v) has two coordinates. FIGURE 12.10 A vector PO in standard position has its initial point at the origin. The directed line segments PQ and v are DEFINITION If v is a two-dimensional vector in the plane equal to the vector parallel and have the same length. with initial point at the origin and terminal point (v, v2). then the component form of v is V = ( V1, U2 )- If v is a three-dimensional vector equal to the vector with initial point at the origin and terminal point (vj, v2, v;), then the component form of v is HISTORICAL BIOGRAPHY So a two-dimensional vector is an ordered pair v = (v1, v2 ) of real numbers, and a Carl Friedrich Gauss three-dimensional vector is an ordered triple v = (Uj, ", u; ) of real numbers. The num- (1777-1855) bers 11, uz, and 13 are the components of v. www .goo.g1/LZMPLA If v = (21, vz, vy) is represented by the directed line segment PO, where the initial point is P(x, 31. 2) and the terminal point is O(x2, )2, 22), then x, + , = x2, v + uz = 3, and 2 + 3 = 2 (see Figure 12.10). Thus, v, = x2 - X1, 12 = 12 - F1, and vy = 2 - 2 are the components of PO. In summary, given the points P(x1. ). 2) and O(x2. )2. z;), the standard position vector v = ( vn, U2. vy) equal to PO is v= ( 1 - * ) - 3.2- 2).If v is two-dimensional with P(x, y) and @(x,, y,) as points in the plane, then v = (12 - 21. )2 - 3) . There is no third component for planar vectors. With this under- standing, we will develop the algebra of three-dimensional vectors and simply drop the third component when the vector is two-dimensional (a planar vector). Two vectors are equal if and only if their standard position vectors are identical. Thus (un, #2, u;) and ( v. v2 v; ) are equal if and only if a = vp, My = v2, and u; = v3. The magnitude or length of the vector PO is the length of any of its equivalent directed line segment representations. In particular, if v = (x2 - X1. )2 - )1. 22 - 2) is the standard position vector for PO, then the distance formula gives the magnitude or length of v, denoted by the symbol | vl or Ivil. The magnitude or length of the vector v = PO is the nonnegative number (see Figure 12.10). The only vector with length 0 is the zero vector 0 = (0, 0) or 0 = (0, 0, 0). This vector is also the only vector with no specific direction.Chapter 12 Vectors and Geometry of Space 12.2 Vectors 721 EXAMPLE 1 Find the (a) component form and (b) length of the vector with initial point P(-3, 4, 1) and terminal point Q(-5, 2, 2). Solution (a) The standard position vector v representing PO has components 1 = 1 - 1 =-5- (-3) =-2, why = 13 - 1 = 2-4= -2, and 1 -2-2-2-1 -1. The component form of PO is v = (-2, -2, 1 ). (b) The length or magnitude of v = PO is F - (a, b) [v| = V(-2) + (-2) + (1) = V9 = 3. -+1 EXAMPLE 2 A small cart is being pulled along a smooth horizontal floor with a FIGURE 12.11 The force pulling the 20-lb force F making a 45" angle to the floor (Figure 12.11). What is the effective force cart forward is represented by the vector F moving the cart forward? whose horizontal component is the effect tive force (Example 2). Solution The effective force is the horizontal component of F = (a. b) , given by a = |F cos 450 = (20)( V2 = 14.14 1b.Notice that F is a two-dimensional vector. Vector Algebra Operations Two principal operations involving vectors are vector addition and scalar multiplication. utv A scalar is simply a real number, and is called such when we want to draw attention to the differences between numbers and vectors, Scalars can be positive, negative, or zero and are used to "scale" a vector by multiplication. (a) DEFINITIONS Let u = (#j. #2. "; ) and v = ( vj. vy, v; ) be vectors with & a scalar. Addition: utv = ( u + up , ly + up, My + us) Scalar multiplication: ku - (kaj. kuz, kus) We add vectors by adding the corresponding components of the vectors. We multiply a vector by a scalar by multiplying each component by the scalar. The definitions also apply to planar vectors, except in that case there are only two components, (wj, w2 ) and ( v1. U2 ). The definition of vector addition is illustrated geometrically for planar vectors in Fig- (b) ure 12.12a, where the initial point of one vector is placed at the terminal point of the other. FIGURE 12.12 (a) Geometric inter- Another interpretation is shown in Figure 12.12b (called the parallelogram law of addi- pretation of the vector sum. (b) The tion), where the sum, called the resultant vector, is the diagonal of the parallelogram. In parallelogram law of vector addition physics, forces add vectorially as do velocities, accelerations, and so on. So the force act- in which both vectors are in standard ing on a particle subject to two gravitational forces, for example, is obtained by adding the position. two force vectors.Chapter 12 Vectors and Geometry of Space 12.2 Vectors 723 { op, = xi + ml + ak Unit Vectors A vector v of length I is called a unit vector. The standard unit vectors are i = (1.0,0), j = (0, 1,0), and k = (0, 0, 1). Any vector v = (vp, vz, v) ) can be written as a linear combination of the standard unit vectors as follows: PP . V= ( VI. 12. v) = (v1. 0,0) + (0. 12.0) + (0. 0. v;) = v ( 1, 0, 0) + 2 (0, 1. 0) + v3 ( 0, 0, 1) =mi+uj+ uk. We call the scalar (or number) up the i-component of the vector v, u, the FIGURE 12.15 The vector from A to j-component, and v; the k-component. As shown in Figure 12.15, the component form Pris RR = (x - x)it (2 - y)j + for the vector from P(x, ), Z) to P(xz, 12, z2) is (2 - 2)k. AR = (2 - x)it on - Mi + (2 - z)k. If v * 0, then its length |v| is not zero and MY = 14151 = 1 . That is. w/ w is a unit vector in the direction of v, called the direction of the nonzero vector v. EXAMPLE 4 Find a unit vector u in the direction of the vector from A(1, 0. 1) to P (3, 2, 0).Solution We divide AP, by its length: AR = (3 - 1)i+ (2 - 0)j + (0 - 1)k = 2i + 2j - k [RAI = V(2) + (2) + (-1) = V4+4+ 1 = V9 =3 PP. 2i + 2j - k 1 = = 3 i + j - K. This unit vector u is the direction of PP- EXAMPLE 5 If v - 3i - 4j is a velocity vector, express v as a product of its speed times its direction of motion. Solution Speed is the magnitude (length) of v: Iv = V(3)- + (-4) = V9 + 16 = 5. HISTORICAL BIOGRAPHY The unit vector v/ v is the direction of v: Hermann Grassmann (1809-1877) V 3i - 4j www. goo. gl/gBHsw0 Ivl 5 J. So v = 31 - 4j = i . Length Direction of motion (speed)