Can someone explain this question. I do not understand

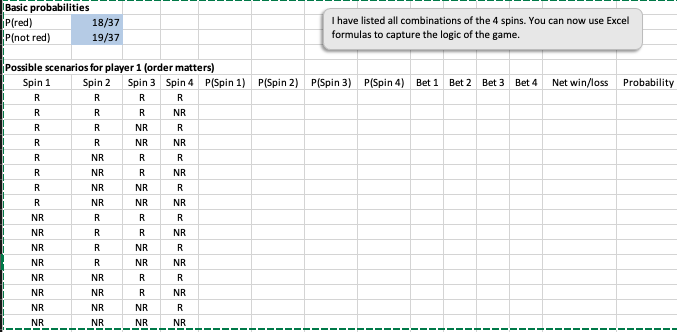
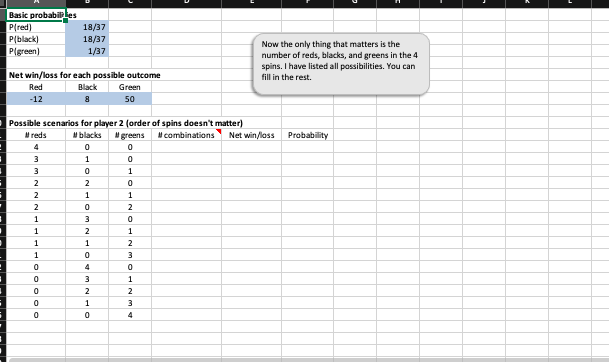
Basic probabilities iP (red) 18/37 I have listed all combinations of the 4 spins. You can now use Excel P(not red) 19/37 formulas to capture the logic of the game. Possible scenarios for player 1 (order matters) Spin 1 Spin 2 Spin 3 Spin 4 P(Spin 1) P(Spin 2) P(Spin 3) P(Spin 4) Bet 1 Bet 2 Bet 3 Bet 4 R Net win/loss R Probability R R R R R NR R R NR R R R NR NR R NR R R R NR R NR R NR NR R R NR NR NR NR R R R NR R R NR NR R NR R NR R NR NR NR NR R R NR NR R NR NR NR NR R NR NR NR NRBasic probabil les P/red] 18/37 P(black] 18/37 Now the only thing that matters is the P(green] 1/37 number of reds, blacks, and greens in the 4 spins. I have listed all possibilities. You can Net win/loss for each possible outcome fill in the rest. Red Black Green -12 50 Possible scenarios for player 2 (order of spins doesn't matter) U reds # blacks greens # combinations * Net win/loss Probability 4 0 1Two gamblers play a version of roulette with a wheel as shown in the file P05_63.xisx. Each gambler places four bets, but their strategies are different, as explained below. For each gambler, use the rules of probability to find the distribution of their net winnings after four bets. Then find the mean and standard deviation of their net winnings. The file gets you started. Round your answers to two decimal places, if necessary and if your answer is negative value, please enter "minus" sign. a. Player 1 always bets on red. On each bet, he either wins or loses what he bets. His first bet is for $10. From then on, he bets $10 following a win, and he doubles his bet after a loss. (This is called a martingale strategy and is used frequently at casinos.) For example, if he spins red, red, not red, and not red, his bets are for $10, $10, $10, and $20, and he has a net loss of $10. Or if he spins not red, not red, not red, and red, then his bets are for $10, $20, $40, and $80, and he has a net gain of $10. Mean Standard Deviation b. Player 2 always bets on black and green. On each bet, he places $10 on black and $2 on green. If red occurs, he loses all $12. If black occurs, he wins a net $8 ($10 gain on black, $2 loss on green). If green occurs, he wins a net $50 ($10 loss on black, $60 gain on green). Mean Standard Deviation $ X