can someone please solve this in scratch and help me out

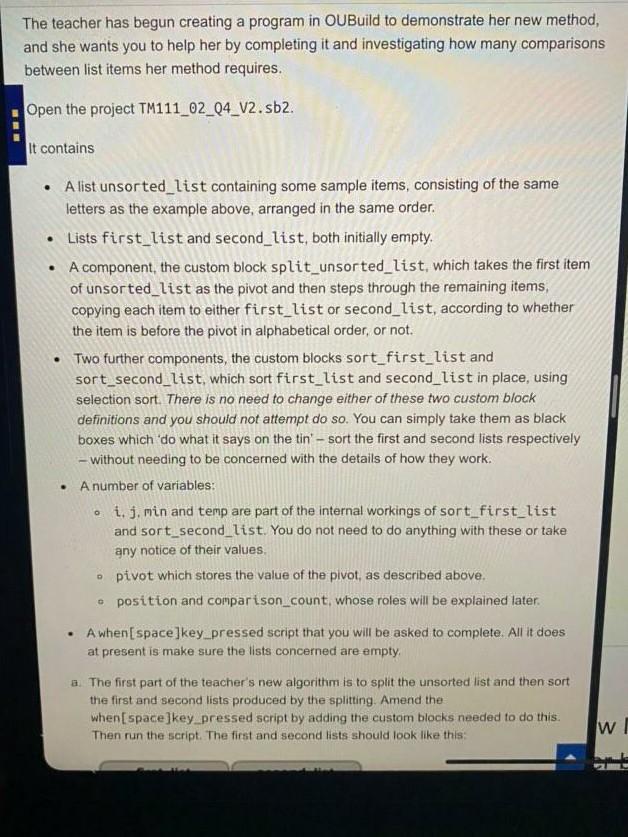
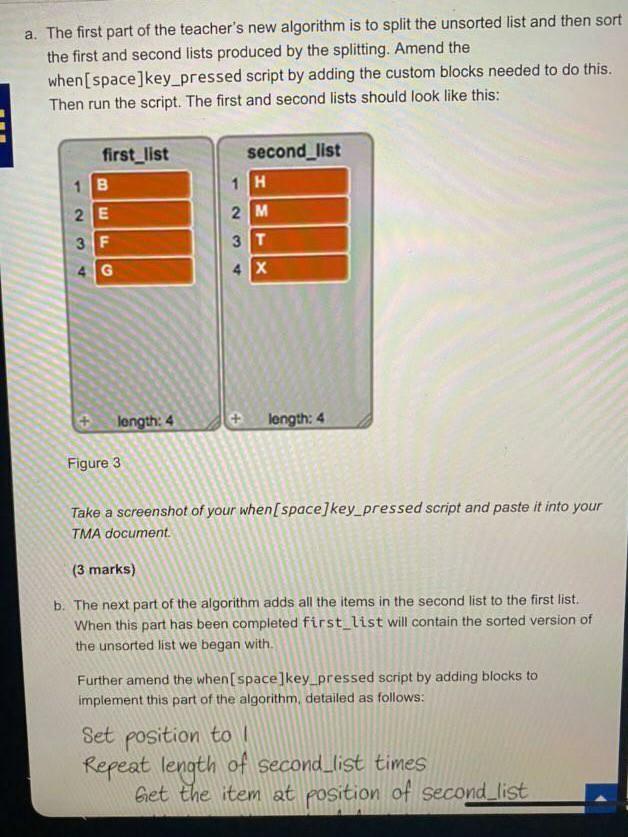
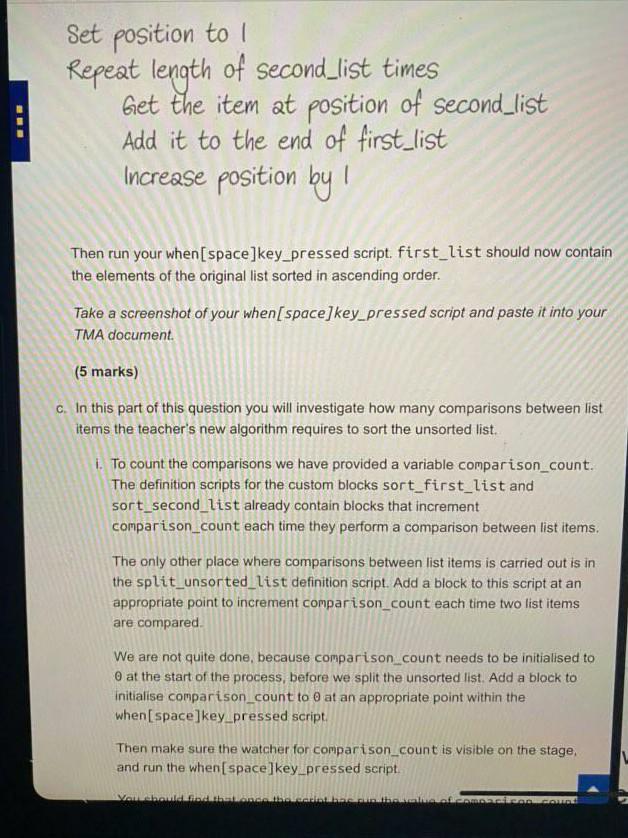
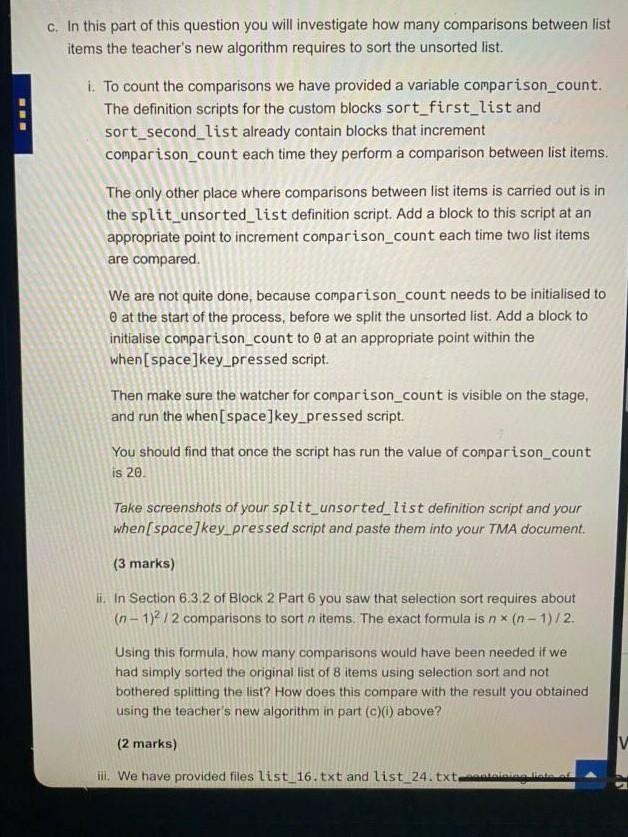
The teacher has begun creating a program in OUBuild to demonstrate her new method, and she wants you to help her by completing it and investigating how many comparisons between list items her method requires. Open the project TM111_02_04_V2. sb2. It contains A list unsorted_list containing some sample items, consisting of the same letters as the example above, arranged in the same order. Lists first_list and second_list, both initially empty. A component, the custom block split_unsorted_list, which takes the first item of unsorted_list as the pivot and then steps through the remaining items, copying each item to either first_list or second_list, according to whether the item is before the pivot in alphabetical order, or not. Two further components, the custom blocks sort_first_list and sort_second_list, which sort first_list and second_list in place, using selection sort. There is no need to change either of these two custom block definitions and you should not attempt do so. You can simply take them as black boxes which do what it says on the tin' - sort the first and second lists respectively - without needing to be concerned with the details of how they work. A number of variables: oi. j. min and temp are part of the internal workings of sort_first_list and sort_second_list. You do not need to do anything with these or take any notice of their values, pivot which stores the value of the pivot as described above. . position and comparison_count, whose roles will be explained later. . A when[space]key pressed script that you will be asked to complete. All it does at present is make sure the lists concerned are empty a. The first part of the teacher's new algorithm is to split the unsorted list and then sort the first and second lists produced by the splitting. Amend the when[space]key pressed script by adding the custom blocks needed to do this. Then run the script. The first and second lists should look like this: WT a. The first part of the teacher's new algorithm is to split the unsorted list and then sort the first and second lists produced by the splitting. Amend the when[space]key_pressed script by adding the custom blocks needed to do this. Then run the script. The first and second lists should look like this: second_list 1 H first_list 1 B 2 E 3 F 2 M 3 T 4 X 4 G length: 4 + length: 4 Figure 3 Take a screenshot of your when[ space]key_pressed script and paste it into your TMA document (3 marks) b. The next part of the algorithm adds all the items in the second list to the first list When this part has been completed first_list will contain the sorted version of the unsorted list we began with Further amend the when[space]key_pressed script by adding blocks to implement this part of the algorithm, detailed as follows: Set position to Repeat length of second_list times Get the item at position of second_list Set position to Repeat length of second_list times Get the item at position of second_list Add it to the end of first_list Increase position by! I Then run your when[space]key_pressed script. first_list should now contain the elements of the original list sorted in ascending order. Take a screenshot of your when[space]key_pressed script and paste it into your TMA document (5 marks) c. In this part of this question you will investigate how many comparisons between list items the teacher's new algorithm requires to sort the unsorted list. 1. To count the comparisons we have provided a variable comparison_count. The definition scripts for the custom blocks sort_first_list and sort_second_list already contain blocks that increment comparison_count each time they perform a comparison between list items. The only other place where comparisons between list items is carried out is in the split_unsorted_list definition script. Add a block to this script at an appropriate point to increment comparison_count each time two list items are compared We are not quite done, because comparison count needs to be initialised to at the start of the process, before we split the unsorted list. Add a block to initialise comparison_count to 0 at an appropriate point within the when space]key_pressed script. Then make sure the watcher for comparison_count is visible on the stage, and run the when[space]key_pressed script Vathaliltinathaananthainthae unhes omnaaraan BE c. In this part of this question you will investigate how many comparisons between list items the teacher's new algorithm requires to sort the unsorted list. 1. To count the comparisons we have provided a variable comparison_count. The definition scripts for the custom blocks sort_first_list and sort_second_list already contain blocks that increment comparison_count each time they perform a comparison between list items. The only other place where comparisons between list items is carried out is in the split_unsorted_list definition script. Add a block to this script at an appropriate point to increment comparison_count each time two list items are compared We are not quite done, because comparison_count needs to be initialised to at the start of the process, before we split the unsorted list. Add a block to initialise comparison_count to 0 at an appropriate point within the when space]key_pressed script. Then make sure the watcher for comparison_count is visible on the stage, and run the when[space]key_pressed script. You should find that once the script has run the value of comparison_count is 20. Take screenshots of your split_unsorted_list definition script and your when[space]key_pressed script and paste them into your TMA document. (3 marks) li. In Section 6.3.2 of Block 2 Part 6 you saw that selection sort requires about (n-1)2/2 comparisons to sort n items. The exact formula is n * (n-1)/2. Using this formula, how many comparisons would have been needed if we had simply sorted the original list of 8 items using selection sort and not bothered splitting the list? How does this compare with the result you obtained using the teacher's new algorithm in part (c)) above? (2 marks) V ill. We have provided files list_16.txt and list_24.txt (3 marks) ii. In Section 6.3.2 of Block 2 Part 6 you saw that selection sort requires about (n-1)2/2 comparisons to sort n items. The exact formula is n * (n-1)/2. Using this formula, how many comparisons would have been needed if we had simply sorted the original list of 8 items using selection sort and not bothered splitting the list? How does this compare with the result you obtained using the teacher's new algorithm in part (c)(I) above? (2 marks) ili. We have provided files list_16.txt and list_24.txt, containing lists of 16 and 24 items respectively. The original list of 8 items is also available as list_8.txt, should you need it again. Import the contents of list_16.txt into unsorted_list, following the procedure described on page 69 of Block 2 Part 4. Run your when[space]key_pressed script and note the number of comparisons taken to sort the 16 items. Repeat this with the file list_24.txt and again note how many comparisons are needed. Then copy the following table into your TMA document and complete it. 8 16 24 Number of items Number of comparisons 20 Do your results indicate that the relationship between the length of the list and the number of comparisons required by the teacher's new sorting strategy is linear or non-linear? Briefly explain your answer (5 marks) V d. On pages 231-232 of Block 2 Part 6 nearly sorted data is discussed, and it is explained that having nearly sorted data is a common situation alia Webvidadosador near or non-linear? breny explain your answer. (5 marks) d. On pages 231-232 of Block 2 Part 6 nearly sorted data is discussed, and it is explained that having nearly sorted data is a common situation. 1. We have provided a file nearly_sorted_list.txt containing a list of 8 items which are nearly sorted. Import the contents of nearly_sorted_list.txt into unsorted_list following the procedure described on page 69 of Block 2 Part 4. Now run your when[space] key_pressed script and note the number of comparisons taken by the teacher's new algorithm. For this list, how does the new sorting algorithm compare with straight selection sort? (2 marks) li. The idea behind the teacher's new algorithm is that selection sort takes more comparisons to sort a single long list than it does to sort two shorter lists each about half the size of the longer list. But with a nearly sorted list the first item is very likely to be before all the others in alphabetical order (as was the case in part (d) above). Using this as the pivot to split the list means the first list will remain empty and all the items will placed in the second list. We will be back to sorting one long list and any advantage gained from sorting smaller lists will be lost. In fact we will have used extra comparisons to split the list, so the performance will be worse than selection sort. To avoid this situation we need to choose a different pivot. One strategy is to choose an item from the middle of the list. That way there is a good chance that about half the items will be smaller and half larger, given that the list is nearly sorted already Modify the the split_unsorted_list definition script so that the pivot is set to the item at or closest to the middle of the list. Find the position of this item by dividing the length of the list by 2, then rounding w The teacher has begun creating a program in OUBuild to demonstrate her new method, and she wants you to help her by completing it and investigating how many comparisons between list items her method requires. Open the project TM111_02_04_V2. sb2. It contains A list unsorted_list containing some sample items, consisting of the same letters as the example above, arranged in the same order. Lists first_list and second_list, both initially empty. A component, the custom block split_unsorted_list, which takes the first item of unsorted_list as the pivot and then steps through the remaining items, copying each item to either first_list or second_list, according to whether the item is before the pivot in alphabetical order, or not. Two further components, the custom blocks sort_first_list and sort_second_list, which sort first_list and second_list in place, using selection sort. There is no need to change either of these two custom block definitions and you should not attempt do so. You can simply take them as black boxes which do what it says on the tin' - sort the first and second lists respectively - without needing to be concerned with the details of how they work. A number of variables: oi. j. min and temp are part of the internal workings of sort_first_list and sort_second_list. You do not need to do anything with these or take any notice of their values, pivot which stores the value of the pivot as described above. . position and comparison_count, whose roles will be explained later. . A when[space]key pressed script that you will be asked to complete. All it does at present is make sure the lists concerned are empty a. The first part of the teacher's new algorithm is to split the unsorted list and then sort the first and second lists produced by the splitting. Amend the when[space]key pressed script by adding the custom blocks needed to do this. Then run the script. The first and second lists should look like this: WT a. The first part of the teacher's new algorithm is to split the unsorted list and then sort the first and second lists produced by the splitting. Amend the when[space]key_pressed script by adding the custom blocks needed to do this. Then run the script. The first and second lists should look like this: second_list 1 H first_list 1 B 2 E 3 F 2 M 3 T 4 X 4 G length: 4 + length: 4 Figure 3 Take a screenshot of your when[ space]key_pressed script and paste it into your TMA document (3 marks) b. The next part of the algorithm adds all the items in the second list to the first list When this part has been completed first_list will contain the sorted version of the unsorted list we began with Further amend the when[space]key_pressed script by adding blocks to implement this part of the algorithm, detailed as follows: Set position to Repeat length of second_list times Get the item at position of second_list Set position to Repeat length of second_list times Get the item at position of second_list Add it to the end of first_list Increase position by! I Then run your when[space]key_pressed script. first_list should now contain the elements of the original list sorted in ascending order. Take a screenshot of your when[space]key_pressed script and paste it into your TMA document (5 marks) c. In this part of this question you will investigate how many comparisons between list items the teacher's new algorithm requires to sort the unsorted list. 1. To count the comparisons we have provided a variable comparison_count. The definition scripts for the custom blocks sort_first_list and sort_second_list already contain blocks that increment comparison_count each time they perform a comparison between list items. The only other place where comparisons between list items is carried out is in the split_unsorted_list definition script. Add a block to this script at an appropriate point to increment comparison_count each time two list items are compared We are not quite done, because comparison count needs to be initialised to at the start of the process, before we split the unsorted list. Add a block to initialise comparison_count to 0 at an appropriate point within the when space]key_pressed script. Then make sure the watcher for comparison_count is visible on the stage, and run the when[space]key_pressed script Vathaliltinathaananthainthae unhes omnaaraan BE c. In this part of this question you will investigate how many comparisons between list items the teacher's new algorithm requires to sort the unsorted list. 1. To count the comparisons we have provided a variable comparison_count. The definition scripts for the custom blocks sort_first_list and sort_second_list already contain blocks that increment comparison_count each time they perform a comparison between list items. The only other place where comparisons between list items is carried out is in the split_unsorted_list definition script. Add a block to this script at an appropriate point to increment comparison_count each time two list items are compared We are not quite done, because comparison_count needs to be initialised to at the start of the process, before we split the unsorted list. Add a block to initialise comparison_count to 0 at an appropriate point within the when space]key_pressed script. Then make sure the watcher for comparison_count is visible on the stage, and run the when[space]key_pressed script. You should find that once the script has run the value of comparison_count is 20. Take screenshots of your split_unsorted_list definition script and your when[space]key_pressed script and paste them into your TMA document. (3 marks) li. In Section 6.3.2 of Block 2 Part 6 you saw that selection sort requires about (n-1)2/2 comparisons to sort n items. The exact formula is n * (n-1)/2. Using this formula, how many comparisons would have been needed if we had simply sorted the original list of 8 items using selection sort and not bothered splitting the list? How does this compare with the result you obtained using the teacher's new algorithm in part (c)) above? (2 marks) V ill. We have provided files list_16.txt and list_24.txt (3 marks) ii. In Section 6.3.2 of Block 2 Part 6 you saw that selection sort requires about (n-1)2/2 comparisons to sort n items. The exact formula is n * (n-1)/2. Using this formula, how many comparisons would have been needed if we had simply sorted the original list of 8 items using selection sort and not bothered splitting the list? How does this compare with the result you obtained using the teacher's new algorithm in part (c)(I) above? (2 marks) ili. We have provided files list_16.txt and list_24.txt, containing lists of 16 and 24 items respectively. The original list of 8 items is also available as list_8.txt, should you need it again. Import the contents of list_16.txt into unsorted_list, following the procedure described on page 69 of Block 2 Part 4. Run your when[space]key_pressed script and note the number of comparisons taken to sort the 16 items. Repeat this with the file list_24.txt and again note how many comparisons are needed. Then copy the following table into your TMA document and complete it. 8 16 24 Number of items Number of comparisons 20 Do your results indicate that the relationship between the length of the list and the number of comparisons required by the teacher's new sorting strategy is linear or non-linear? Briefly explain your answer (5 marks) V d. On pages 231-232 of Block 2 Part 6 nearly sorted data is discussed, and it is explained that having nearly sorted data is a common situation alia Webvidadosador near or non-linear? breny explain your answer. (5 marks) d. On pages 231-232 of Block 2 Part 6 nearly sorted data is discussed, and it is explained that having nearly sorted data is a common situation. 1. We have provided a file nearly_sorted_list.txt containing a list of 8 items which are nearly sorted. Import the contents of nearly_sorted_list.txt into unsorted_list following the procedure described on page 69 of Block 2 Part 4. Now run your when[space] key_pressed script and note the number of comparisons taken by the teacher's new algorithm. For this list, how does the new sorting algorithm compare with straight selection sort? (2 marks) li. The idea behind the teacher's new algorithm is that selection sort takes more comparisons to sort a single long list than it does to sort two shorter lists each about half the size of the longer list. But with a nearly sorted list the first item is very likely to be before all the others in alphabetical order (as was the case in part (d) above). Using this as the pivot to split the list means the first list will remain empty and all the items will placed in the second list. We will be back to sorting one long list and any advantage gained from sorting smaller lists will be lost. In fact we will have used extra comparisons to split the list, so the performance will be worse than selection sort. To avoid this situation we need to choose a different pivot. One strategy is to choose an item from the middle of the list. That way there is a good chance that about half the items will be smaller and half larger, given that the list is nearly sorted already Modify the the split_unsorted_list definition script so that the pivot is set to the item at or closest to the middle of the list. Find the position of this item by dividing the length of the list by 2, then rounding w