Can u help me please for tMDL100 this all information i dont have more 
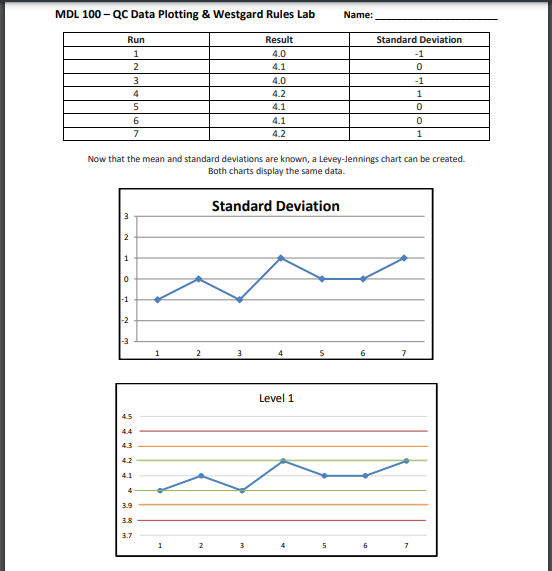
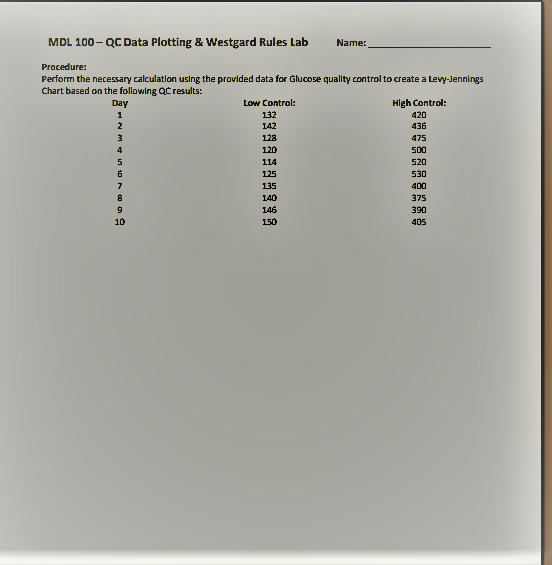
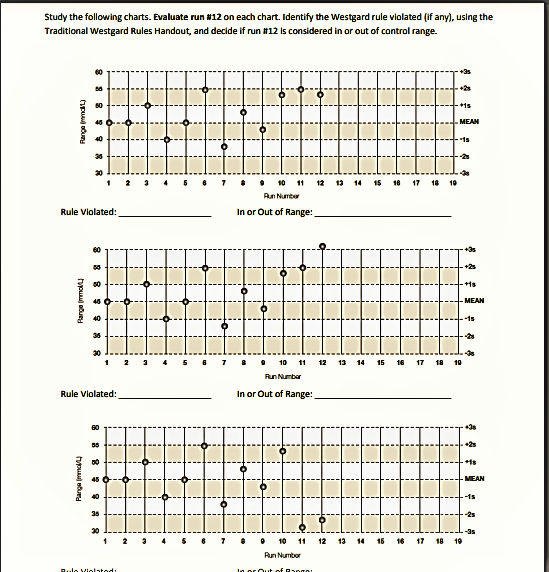
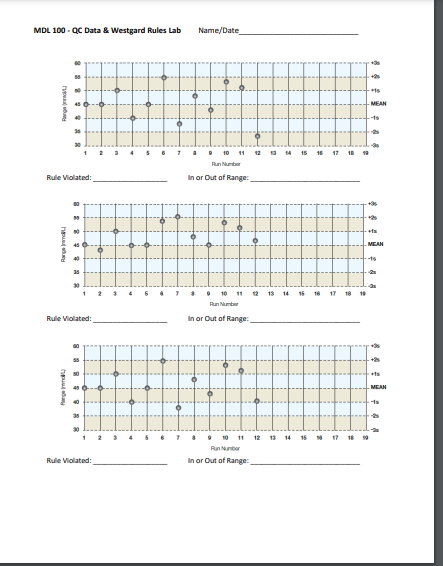
MDL 100 - QC Data Plotting & Westgard Rules Lab Name: QC statistics for each test performed in the laboratory are calculated from the QC database collected by regular testing of control products. The data collected is specific for each level of control. Consequently, the statistics and ranges calculated from this data are also specific for each level of control and reflect the behavior of the test at specific concentrations. The most fundamental statistics used by the laboratory are the mean (I) and standard deviation (s). The mean (or average) is the laboratory's best estimate of the analyte's true value for a specific level of control. To calculate a mean for a specific level of control, add all the values collected for that control. Then divide the sum of these values by the total number of values. For instance, to calculate the mean for a normal control (Level 1), find the sum () of the data (4.0, 4.1, 4.0, 4.2, 4.1, 4.1, 4.2). The sum () is 28.7 mmol/L. The number of values is 7 (n = 7). Therefore, the mean for the normal control is 4.1 mmol/L (or 28.7 mmol/L divided by 7). Standard deviation is a statistic that quantifies how close numerical values (ie., Qc values are in relation to each other. Standard deviation is calculated for control products from the same data used to calculate the mean. It provides the laboratory an estimate of test consistency at specific concentrations. The repeatability of a test may be consistent (low standard deviation) or inconsistent (high standard deviation). Inconsistent repeatability may be due to the chemistry involved or to a malfunction. If it is a malfunction, the laboratory must correct the problem. It is desirable to get repeated measurements of the same specimen as close as possible. Standard deviation is calculated by: Where: S = standard deviation (x - 5)2 = mean (average) of the QC values SE [(x - 2)2 = the sum of the squares of (differences between individual QC values and the mean) n-1 n=the number of values in the data set To calculate the standard deviation from the data used earlier: (4.0, 4.1, 4.0, 4.2, 4.1, 4.1, 4.2} (x = 4.1, n = 7) (x - 2)2 S = -1 (4.0 - 4.1)2 + (4.1 - 1.1)2+(4.0 - 4.1)2 + (4.2 - 4.1)2 + (4.1 - 4.1)2 + (4.1 - 4.1)2 + (4.2 - 4.1) 7-1 SS (-0.1)2 + (0.0)2 + (-0.1)2 + (0.1)2 + (0.0)2 + (0.0)2 + (0.1)2 6 S = 0.04 6 5 = 0.082, or 0.1 (rounded to significant figures) One (1) standard deviation = R1 0.1 or calculate the standard deviation of each run's result with (result - x)/s. MDL 100 - QC Data Plotting & Westgard Rules Lab Name: Run 1 2 3 4 5 6 7 Result 4.0 4.1 4.0 4.2 4.1 4.1 4.2 Standard Deviation - 1 0 -1 1 0 0 1 Now that the mean and standard deviations are known, a Levey-Jennings chart can be created. Both charts display the same data. Standard Deviation 2 1 0 -1 -2 -3 2 3 4 5 6 7 Level 1 4.5 4.3 4.2 4.1 3.9 3.8 3.7 1 Low Control 0 2 4 6 8 10 12 14 High Control 2 8 10 12 14 MDL 100-QC Data Plotting & Westgard Rules Lab Name: Procedure: Perform the necessary calculation using the provided data for Glucose quality control to create a Levy-Jennings Chart based on the following QC results: Day Low Control: High Control: 1 2 3 4 5 132 142 128 120 114 125 135 140 146 150 420 436 475 500 520 530 400 375 390 405 9 10 Study the following charts. Evaluate run #12 on each chart. Identify the Westgard rule violated (if any), using the Traditional Westgard Rules Handout, and decide if run #12 is considered in or out of control range. +2 - +15 (UAS) Sri MEAN 10 15 18 10 10 11 12 13 14 Pun Nurcer In or Out of Range: Rule Violated: +18 Pargo polu - MEAN SR 10 11 12 13 14 15 16 17 10 Run Number In or Out of Range: Rule Violated: +18 Rarged - MEAN -15 35 30 ON 1 17 18 19 10 11 12 13 14 15 16 Run Number la viol la Art A MDL 100 - QC Data & Westgard Rules Lab Name/Date MAN - MEAN 15 1710 10 Run Number In or Out of Range Rule Violated: Har du MEAN 1s 2 18 14 18 19 10 Run Number Rule Violated: In or Out of Range 8 MEAN Marge - 1 3 4 5 6 7 16 17 18 9 10 11 12 13 14 Run In or Out of Range: Rule Violated: MDL 100 - QC Data Plotting & Westgard Rules Lab Name: QC statistics for each test performed in the laboratory are calculated from the QC database collected by regular testing of control products. The data collected is specific for each level of control. Consequently, the statistics and ranges calculated from this data are also specific for each level of control and reflect the behavior of the test at specific concentrations. The most fundamental statistics used by the laboratory are the mean (I) and standard deviation (s). The mean (or average) is the laboratory's best estimate of the analyte's true value for a specific level of control. To calculate a mean for a specific level of control, add all the values collected for that control. Then divide the sum of these values by the total number of values. For instance, to calculate the mean for a normal control (Level 1), find the sum () of the data (4.0, 4.1, 4.0, 4.2, 4.1, 4.1, 4.2). The sum () is 28.7 mmol/L. The number of values is 7 (n = 7). Therefore, the mean for the normal control is 4.1 mmol/L (or 28.7 mmol/L divided by 7). Standard deviation is a statistic that quantifies how close numerical values (ie., Qc values are in relation to each other. Standard deviation is calculated for control products from the same data used to calculate the mean. It provides the laboratory an estimate of test consistency at specific concentrations. The repeatability of a test may be consistent (low standard deviation) or inconsistent (high standard deviation). Inconsistent repeatability may be due to the chemistry involved or to a malfunction. If it is a malfunction, the laboratory must correct the problem. It is desirable to get repeated measurements of the same specimen as close as possible. Standard deviation is calculated by: Where: S = standard deviation (x - 5)2 = mean (average) of the QC values SE [(x - 2)2 = the sum of the squares of (differences between individual QC values and the mean) n-1 n=the number of values in the data set To calculate the standard deviation from the data used earlier: (4.0, 4.1, 4.0, 4.2, 4.1, 4.1, 4.2} (x = 4.1, n = 7) (x - 2)2 S = -1 (4.0 - 4.1)2 + (4.1 - 1.1)2+(4.0 - 4.1)2 + (4.2 - 4.1)2 + (4.1 - 4.1)2 + (4.1 - 4.1)2 + (4.2 - 4.1) 7-1 SS (-0.1)2 + (0.0)2 + (-0.1)2 + (0.1)2 + (0.0)2 + (0.0)2 + (0.1)2 6 S = 0.04 6 5 = 0.082, or 0.1 (rounded to significant figures) One (1) standard deviation = R1 0.1 or calculate the standard deviation of each run's result with (result - x)/s. MDL 100 - QC Data Plotting & Westgard Rules Lab Name: Run 1 2 3 4 5 6 7 Result 4.0 4.1 4.0 4.2 4.1 4.1 4.2 Standard Deviation - 1 0 -1 1 0 0 1 Now that the mean and standard deviations are known, a Levey-Jennings chart can be created. Both charts display the same data. Standard Deviation 2 1 0 -1 -2 -3 2 3 4 5 6 7 Level 1 4.5 4.3 4.2 4.1 3.9 3.8 3.7 1 Low Control 0 2 4 6 8 10 12 14 High Control 2 8 10 12 14 MDL 100-QC Data Plotting & Westgard Rules Lab Name: Procedure: Perform the necessary calculation using the provided data for Glucose quality control to create a Levy-Jennings Chart based on the following QC results: Day Low Control: High Control: 1 2 3 4 5 132 142 128 120 114 125 135 140 146 150 420 436 475 500 520 530 400 375 390 405 9 10 Study the following charts. Evaluate run #12 on each chart. Identify the Westgard rule violated (if any), using the Traditional Westgard Rules Handout, and decide if run #12 is considered in or out of control range. +2 - +15 (UAS) Sri MEAN 10 15 18 10 10 11 12 13 14 Pun Nurcer In or Out of Range: Rule Violated: +18 Pargo polu - MEAN SR 10 11 12 13 14 15 16 17 10 Run Number In or Out of Range: Rule Violated: +18 Rarged - MEAN -15 35 30 ON 1 17 18 19 10 11 12 13 14 15 16 Run Number la viol la Art A MDL 100 - QC Data & Westgard Rules Lab Name/Date MAN - MEAN 15 1710 10 Run Number In or Out of Range Rule Violated: Har du MEAN 1s 2 18 14 18 19 10 Run Number Rule Violated: In or Out of Range 8 MEAN Marge - 1 3 4 5 6 7 16 17 18 9 10 11 12 13 14 Run In or Out of Range: Rule Violated












