can you help me understand this question please

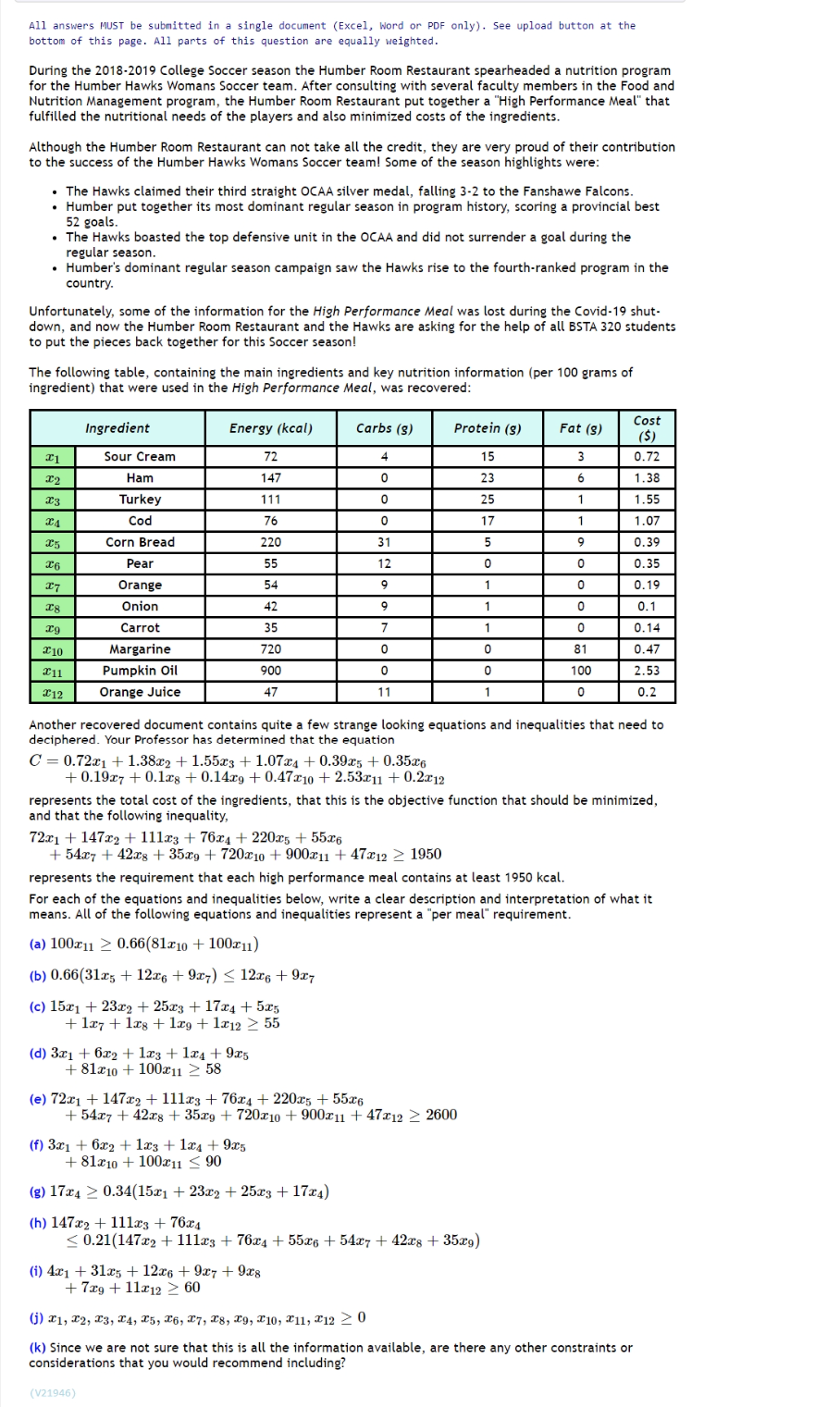
All answers MUST be submitted in a single document (Excel, Hood or PDF only). See upload button. at the bottom of this page. all parts of this question are equallyI weighted. During the 2013-2019 College Soccer season the Humber Room Restaurant spearheaded a nutrition program for the Humber Hawks woman: soccer team. After consulting with several facultyr members in the Food and Nutrition Management program. the Humber Room Restaurant put together a \"High Performance Meal" that fulfilled the nutritional needs of the players and also minimized costs of the ingredients. Although the Humber Room Restaurant can not take all the credit, theyI are very:r proud of their contribution to the success of the Humber Hawks Womans Soccer teaml Some of the season highlights were: - The Hawks claimed their third straight OCM silver medal. falling 3-2 to the Fanshawe Falcons. e Humber put together its most dominant regular season in program history, scoring a provincial best 52 goals. I The Hawks boasted the top defensive unit in the OCAA and did not surrender a goal during the regular season. a Humber's dominant regular season campaign saw the Hawks rise to the fourth-ranked program in the country. Unfortunately. some of the information for the High Performance nieo! was lost during the Covid-19 shut- down, and now the Humber Room Restaurant and the Hawks are asking for the help of all ESTA 320 students to put the pieces back together for this Soccer season! The following table, containing the main ingredients and key nutrition information (per 100 grams of ingredient) that were used in the High Performance Meal. was recovered: M- m-I---m Another recovered document contains quite a few strange looking equations and inequalities that need to deciphered. Your Professor has determined that the equation 0' = 0.72:1 + 1.38:2 + 1.55:3 + 1.073.. + 0.3925 + 0.35311 + 0.19:7 + 0.129 + 0.1.1.:9 + 0.47210 + 253:1: + 0.2::12 represents the total cost of the ingredients, that this is the objective function that should be minimized, and that the following inequality. 723:1 + 14722 + 11132:; + 76:54 + 22035 + 553:5 + 549:7 + 422:3 + 353:9 + 720310 + 900311 + 47312 3 1950 represents the requirement that each high performance meal contains at least 1950 kcal. For each of the equations and inequalities below, write a clear description and interpretation of what it means. All of the following equations and inequalities represent a 'per meal" requirement. (a) 10011] 2 U.55(31210 + 100211) (b) 0.66{3125 + 12236 + 927) S 121'\" + 91? to) 15.131 + 2322 + 25:23 + 172:4 + 535 + 1:37 + 11:5 + 13:9 + 1212 2 55 (d) 3:121 + 02:2 + 1x3 + 134 + 935 + 81210 + 1.00311 2 53 to) 72:1 + 14732 + 11133 + 7634 + 22035 + 5535 + 541:? + 4223 + 359:9 + 720210 + 900311 + 472:1; 2 21600 {f} 3x1 + 6m + 12:; + 1:04 + 92:: + 812310 + 100311 1: 90 (g) 172:4 2'; 0.34{152:1 + 233:2 + 2533 + 173:4) (h) 1473:; + 111133 + 762:4 E {1.21[147:c2 + 111:3: + 762:4 + 552:5 + 542:7 + 423:3 + 352:9] (II 4:51 + 3135 + 12:35 + 93:7 + 92:3 + 72:9 + 11112 2 50 {j} 211 '22! \"1241:53 :35) 373331391 310) R311: 312 Z 0 (It) Since we are not sure that this is all the information available, are there any:r other constraints or considerations that you would recommend including