can you help with parts a-c?

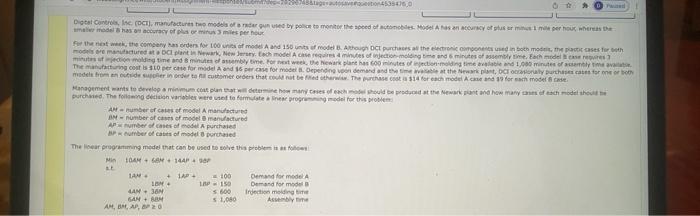
g435660 Digital Contine. (OCT, manufactures to model of ander une by police to monitor the weed codes. As an accuracy of us are per hour whereas the model has as accuracy of his miles per hour For the netw, the company has orders for its of maand 150 unts mode BAROC purchases at the crowd in both mothes for both more matured to parti Newark, New Jersey. Each model che regards of injection molding and minutes of teachers mi-molding time and its some for week, the Newark plane hestes con molding time and 1.000 minutes of The most is $10 perc for model And percase for model Depending on demand and weather stay this cates for made from sucher in detail cutter orders that not be thew The 514 for each model and 19 for en mode Management wants to develop a minimum contra el determine how many tries of could be products that how mary coach model thote purchase. The following decision alles were to formulate the program model for this problem Number of consor model Amandatured A number of cases of model manucured Ambroses of model purchased Pumber of cases of model purchased The linear programming model that can be used to solve this problem to Min 10AM + +1441 LAM 14 Demand for model IBM 1150 Demand for model LAN - 36 5600 Injection melding time 54 + A 5 1.080 Aby AN, BMP, 20 100 Refer to the computer solution below. otimal jestive Value - 2170.60000 Vah Value 100.000 Odos Sed est 0.00000 0.00000 1.25000 10.0000 AP 0.000 DODO Constraint TOUTE 0.00100 06000 Dual VALUE -2.25000 ->.00000 0.00000 0.17500 20.00000 0.01000 Varble Otive Cattelan 30.00000 ODDDD 14.000 3.00000 WY Allowable Increase 1.95000 3.00000 Intimit Allowable Deco Infinite CEEEEE AP 1.75000 3.00000 ... TORTY Constant Allobre Decrease 100.00000 1 POLE Value TOD:00000 150.00 600.000 1.000.00000 2 Increase 11.25 Latit Intit 33.33 000000 20.00000 419.00000 ( Interpret the range of optimality for the objective function coeficent Ott a single change to the injection molding time or assembly time for either model care is within the allowable range, the optimal solution will not change Ir multiple changes are made to the manufacturing or purchase costs for either model case within their respective aliowable ranges, the optimal solution will not change If multiple changes we made to the injection molding time or assembly time for other model case within the respective allowable ranges, the optimal solution will not change Of a single change to the manufacturing cost or purchase cost for other model cases within the lowanie range, the optimal soation will not change (b) Suppose that the manufacturing cost increases to $11:10 per case for model A would the optimal solution change? Yes, it is necessary to solve the model again No, the optimal solution remains the same What is the optimal solution? 2170 at (AM, BM, AP.BP) - 11.2.5,14,9 X ) (c) Suppose that the manufacturing cost increases to $11.30 per case for model and the manufacturing cost for model decreases to $5 per unit. Would the optimal solution change? Yes, it is necessary to solve the model again No, the smaltion remains the same What is the new optimal solution 2210 (AM, BM, AP, Bo (0,135,100,18) g435660 Digital Contine. (OCT, manufactures to model of ander une by police to monitor the weed codes. As an accuracy of us are per hour whereas the model has as accuracy of his miles per hour For the netw, the company has orders for its of maand 150 unts mode BAROC purchases at the crowd in both mothes for both more matured to parti Newark, New Jersey. Each model che regards of injection molding and minutes of teachers mi-molding time and its some for week, the Newark plane hestes con molding time and 1.000 minutes of The most is $10 perc for model And percase for model Depending on demand and weather stay this cates for made from sucher in detail cutter orders that not be thew The 514 for each model and 19 for en mode Management wants to develop a minimum contra el determine how many tries of could be products that how mary coach model thote purchase. The following decision alles were to formulate the program model for this problem Number of consor model Amandatured A number of cases of model manucured Ambroses of model purchased Pumber of cases of model purchased The linear programming model that can be used to solve this problem to Min 10AM + +1441 LAM 14 Demand for model IBM 1150 Demand for model LAN - 36 5600 Injection melding time 54 + A 5 1.080 Aby AN, BMP, 20 100 Refer to the computer solution below. otimal jestive Value - 2170.60000 Vah Value 100.000 Odos Sed est 0.00000 0.00000 1.25000 10.0000 AP 0.000 DODO Constraint TOUTE 0.00100 06000 Dual VALUE -2.25000 ->.00000 0.00000 0.17500 20.00000 0.01000 Varble Otive Cattelan 30.00000 ODDDD 14.000 3.00000 WY Allowable Increase 1.95000 3.00000 Intimit Allowable Deco Infinite CEEEEE AP 1.75000 3.00000 ... TORTY Constant Allobre Decrease 100.00000 1 POLE Value TOD:00000 150.00 600.000 1.000.00000 2 Increase 11.25 Latit Intit 33.33 000000 20.00000 419.00000 ( Interpret the range of optimality for the objective function coeficent Ott a single change to the injection molding time or assembly time for either model care is within the allowable range, the optimal solution will not change Ir multiple changes are made to the manufacturing or purchase costs for either model case within their respective aliowable ranges, the optimal solution will not change If multiple changes we made to the injection molding time or assembly time for other model case within the respective allowable ranges, the optimal solution will not change Of a single change to the manufacturing cost or purchase cost for other model cases within the lowanie range, the optimal soation will not change (b) Suppose that the manufacturing cost increases to $11:10 per case for model A would the optimal solution change? Yes, it is necessary to solve the model again No, the optimal solution remains the same What is the optimal solution? 2170 at (AM, BM, AP.BP) - 11.2.5,14,9 X ) (c) Suppose that the manufacturing cost increases to $11.30 per case for model and the manufacturing cost for model decreases to $5 per unit. Would the optimal solution change? Yes, it is necessary to solve the model again No, the smaltion remains the same What is the new optimal solution 2210 (AM, BM, AP, Bo (0,135,100,18)