Can you please help me. I do not understand these questions. The questions are #1-9.

PLEASE PLEASE I DO NOT HAVE ANY OTHER MATERIAL OF REFERENCE INFORMATION!! ALL THE INFORMATION YOU NEED IS DOWN BELOW.

QUESTIONS ARE DOWN BELOW:

1.

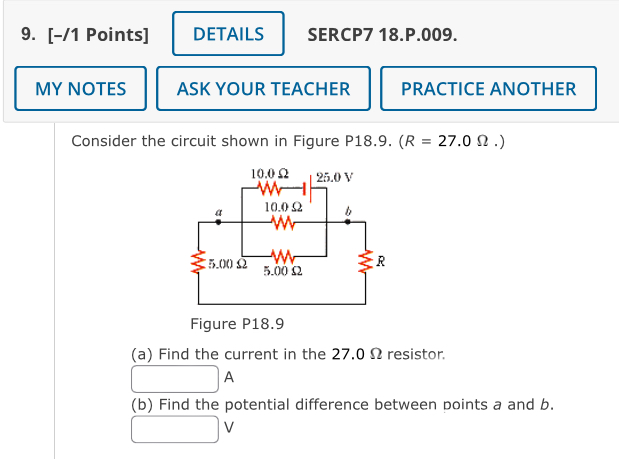
1. [-/1 Points] DETAILS SERCP7 18.AE.01. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Example 18.1 Four Resistors in Series Goal Analyze several resistors connected in series. www Ww WWW R1 R2 Rg RA Req Problem Four resistors are arranged as shown in Figure 18.5a, where R1 = 1.8 0, R2 = 3.6 0, R3 = 4.5 0, and R4 = 6.3 0. Find (a) the equivalent resistance of the circuit and (b) the current in the circuit if the emf of the battery is 6.0 V. (a) 6.0 V (b) 6.0 V Strategy Because the resistors are connected in Figure 18.5 (a) Four resistors connected in series. (b) series, summing their resistances gives the The equivalent resistance of the circuit in (a). equivalent resistance. Ohm's law can be used to find the current. Solution (a) Find the equivalent resistance of the circuit. Apply Equation 18.4, summing the resistances. Reg = R1 + R2 + R3 + R4 = 1.80 + 3.60 + 4.50 + 6.30 Reg = (b) Find the current in the circuit. Apply Ohm's law to the equivalent resistor in AV V Figure 18.5b, solving for the current. 1 = 7 Reg Req = A Exercise 18.1 Hints: Getting Started | I'm Stuck Because the current in the equivalent resistor is 0.370 A, this must also be the current in each resistor of the original circuit. Find the voltage drop across each resistor. AV1.8 0 = AV 3.6 12 = AV4.5 0 = AV6.3 0 =Active Example 18-1 e Refer back to the example, and make sure you can follow the solution to obtain the correct values for the equivalent resistance of the series combination of resistors and for the current through the series. What factors affect the potential difference across a resistor? Self Check: How do the individual potential differences compare to the total potential difference across the series combination? e Reread pages 592-594. Example 18.2 Three Resistors in Parallel Goal Analyze a circuit having resistors connected in parallel. Problem Three resistors are connected in parallel as in Figure 28.7. A potential difference of 18 V is maintained between points a and b. (a) Find the current in each resistor. (b) Calculate the power delivered to each resistor and the total power. (c) Find the equivalent resistance of the circuit. (d) Find the total power delivered to the equivalent resistance. Strategy We can use Ohm's law and the fact that the voltage drops across parallel resistors are all the same to get the current in each resistor. The rest of the problem just requires substitution into the equation for power delivered to a resistor, # = I'R, and the reciprocal-sum law for parallel resistors. Figure 18.7 (Example 18.2) Three resistors connected in parallel. The voltage across each resistor is 18 V. (a) Find the current in each resistor. Apply Ohm's law, solve for the current I I AV 18V delivered by the battery to find the current in YT R T 300 each resistor. l B :] A I AV 18\\ AV 18V TR O (b) Calculate the power delivered to each resistor and the total power. Apply P = I2R to each resistor, substituting the 3 Q: P, = I;2R, = (I)%(3.0 ) = {: w results from part (a). 6 Q: Py = I,2R, = (I,)%(6.0 Q) = :} w 9 Py = I32Ry = (I13)2(9.0 Q) = S w Sum to get the total power. Pt =P1+ Py + Py = S x 102 W (c) Find the equivalent resistance of the circuit. Apply the reciprocal-sum rule, Equation 18.6. 1 _ l L i Req 1 R Ry 1 1 1 111 Req 3.0 6.0 9.0 T 180 18 Req = =02 ST e (d) Compute the power dissipated by the equivalent resistance. Use the alternate power equation. p [Al'}g (18 \\")2 Remarks There's something important to notice in part (a): the smallest 3.0 resistor carries the largest current, while the other, larger resistors of 6.0 and 9.0 carry smaller currents. The largest current is always found in the path of least resistance. In part (b), the power could also be found with ? = (AV)2/R. Note that Py = 108 W, but is rounded to 110 W because there are only two significant figures. Finally, notice that the total power dissipated in the equivalent resistor is the same as the sum of the power dissipated in the individual resistors, as it should be. Exercise 18.2 Hints: Getting Started | I'm Stuck Suppose the resistances in the example are 2.4 2, 4.8 2 and 7.2 (2, respectively, and a new voltage source is provided. If the current measured in the 7.2 Q resistor is 3.0 A, find (a) the potential difference provided by the new battery, and the currents in each of the remaining resistors, (b) the power delivered to each resistor, and the total power, (c) the equivalent resistance, and (d) the total current, and the power dissipated by the equivalent resistor. @e-y Active Example 18-2 * Refer back to the example, and make sure you can follow the solution to obtain the correct values for the current through each resistor, the power dissipated by each resistor, the equivalent resistance of the circuit and the power dissipated by the circuit as a whole. What factors affect the current through a resistor? e \\What factors affect the power dissipated by a resistor? Reread pages 596-597. Example 18.3 Equivalent Resistance Goal Solve a problem involving both series and parallel resistors. Problem Four resistors are connected as shown in Figure 18.11a. (a) Find the equivalent resistance between points a and c. (b) What is the current in each resistor if a 42 V battery is connected between a and c? Strategy Reduce the circuit steps, as shown in Figures 18.11 b and 18.11 , using the sum rule for resistors in series and the reciprocal-sum rule for resistors in parallel. Finding the currents is a matter of applying Ohm's law while working backwards through the diagrams. Solution (a) Find the equivalent resistance of the circuit. The 8.0 2 and 4.0 2 resistors are in series, so use the sum rule to find the equivalent resistance between a and b. The 6.0 2 and 3.0 2 resistors are in parallel, so use the reciprocal-sum rule to find the equivalent resistance between b and (don't forget to invert!) In the new diagram, 18.11b, there are now two resistors in series. Combine them with the sum rule to find the equivalent resistance of the circuit. (b) Find the current in each resistor if a 42 V battery is connected between points a and c. Find the current in the equivalent resistor in Figure 8.11c, which is the total current. Resistors in series all carry the same current, so this is the current in the 12 2 in Figure 8.11b, and also in the 8.0 {2 and 4.0 resistors in Figure 8.11a. Apply the junction rule to point b. The 6.0 2 and 3.0 2 resistors are in parallel, so the voltage drops across them are the same. Substitute this result into Equation (1), with I = 3.0 A. 0 R0 1.0 02 100 Figure 18.11 (Example 18.3) The four resistors shown in (a) can be reduced in steps to an equivalent 14 resistor. Req =Ry +R;=8.002+400=120 1 Req - R R 1 1 + Ry =200 Req=R1+R2=129+2.OQ=(:Q = AV, 42V 1 2.0 1 6.0 + 3.0 e e (WI=I+1I, AVGQ = AV3Q > 201, = I, 3.0A=I;+2I, =3I, 11=[:A (6.0, = (3.0, 5:51PM Mon Mar 18 N RCET VARl ] # webassign.net Remarks As a final check, note that AV, = (6.0 Q)I; = (3.0 2)I; = 6.0 V and AV, = (12 2)I; = 36 V; therefore, AV,. = AV, + AVy. = 42, as expected. N Exercise 18.3 Hints: Getting Started | I'm Stuck I ' Suppose the series resistors in Example 18.3 are now 4.00 2 and 8.00 2 while the parallel resistors are 2.00 2 (top) and 4.00 2 (bottom), and the battery provides an emf of 30.0 V. Find (a) the equivalent resistance and (b) the currents I, Iy, I>. @ =)o - s 4. [-/1 Points] SERCP7 18.P.002.SOLN. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER A 4.0 (1 resistor, an 8.0 {2 resistor, and a 13 {2 resistor are connected in series with a 30 V battery. (a) What is the equivalent resistance? 0 (b) What are the currents in each resistor? A (4.0 Q resistor) A (8.0 resistor) A (13 resistor) (c) Repeat for the case in which all three resistors are connected in parallel across the battery. {1 (equivalent resistance) A (4.0 resistor) A (8.0 1 resistor) A (13 2 resistor) 5. [-/1 Points] DETAILS SERCP7 18.P.005. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER {a) Find the equivalent resistance between points a and b in Figure P18.5 (R = 15.0 1). [ {b) A potential difference of 34.0 V is applied between points @ and b. Calculate the current in each resistor. raoo= A 1(7.00Q)= A I1(15.0 Q) =| A 1(3.00Q)= A 7.00 2 4.00Q 9.00 Q - O i Figure P18.5 6. [-/1 Points] DETAILS SERCP7 18.P.006.SOLN. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the equivalent resistance of the circuit in Figure P18.6. (Ry = 20}, R, = 10 Q) . Figure P18.6 __Submit Answer_| 7. [-/1 Points] DETAILS SERCP7 18.P.008. MY NOTES ASKYOUR TEACHER PRACTICE ANOTHER (a) Find the equivalent resistance of the circuit in Figure P18.8. (R; = 4.00 }, R, = 13.0 ) L Je {b) If the total power supplied to the circuit is 10.00 W, find the emf of the battery. L v R | 1.00 0 & " 5.00 Q) R, | MW Figure P18.8 8. [-/1 Points] DETAILS SERCP7 18.P.010.SOLN. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Two resistors, A and B, are connected in parallel across a 5.0 V battery. The current through B is found to be 1.0 A, When the two resistors are connected in series to the 5.0 V battery, a voltmeter connected across resistor A measures a voltage of 3.8 V. Find the resistances A and B. Ry = Q Ry = )it 9. [-/1 Points] DETAILS SERCP7 18.P.009. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Consider the circuit shown in Figure P18.9. (R = 27.0 1 .) 1002 w50V 10.40 2 Figure P18.9 (a) Find the current in the 27.0 resistor. A (b) Find the potential difference between points a and b. [v