Case 1 Matlab

Code to call function:

% -------------------------------------------------------------------------

% Case 1: Given a history of weekly sales data,

% estimate likely longterm average sales and variability.

% INPUTS:

% nweeks, number of weeks of sales data

% salesSet, set of weekly sales data

% binEdges, bin boundaries: min to max in uniform width (see binCounts)

% OUTPUTS:

% salesAvg, mean of weekly sales

% salesStdDev, standard deviation of weekly sales

% binCounts, salesSet1 data sorted into bins (see binEdges)

% -------------------------------------------------------------------------

% SETUP SECTION -----------------------------------------------------------

% generate the sales data

nweeks= 52;

mu= 1000; % sales average per week

sigma= 100; % sales standard deviation

load('salesSet.mat'); % distribution data

% set up histogram structure

binEdgemin= 500;

binEdgemax= 1500;

binwidth= 100;

binEdges= binEdgemin:binwidth:binEdgemax; % row vec [5500,600,700,...]

% SIMULATION SECTION ------------------------------------------------------

[salesAvg,salesStdDev,binCounts]=Sales_1_fcn(nweeks,salesSet,binEdges);

% REPORT SECTION -------------------------------------------------------

fprintf(' Setup 1: ');

fprintf(' nweeks=%5.0f ',nweeks);

fprintf(' mu= %5.0f ',mu); % mean of normal distrib for sales

fprintf(' sigma= %5.0f ',sigma); % std dev for sales

% results

fprintf(' Results 1: ');

fprintf(' salesAvg= %6.0f ',salesAvg);

fprintf(' salesStdDev=%6.0f ',salesStdDev);

salesMin= min(salesSet);

fprintf(' sales min= %6.0f ',salesMin);

salesMax= max(salesSet);

fprintf(' sales max= %6.0f ',salesMax);

nbins= length(binCounts);

fmta= [' binCounts= [',repmat('%4.0f',1,nbins),'] '];

fprintf(fmta,binCounts(1:nbins));

% figures to aid interpretation of results

figure(1)

x= 1:nweeks;

plot(x,salesSet);

title('Fig.1. History of weekly sales')

xlabel('weeks');

ylabel('sales');

grid on;

%pause

figure(2)

histogram(salesSet,binEdges);

title('Fig.2. Histogram of sales history');

grid on;

fprintf(' ');

% -------------------------------------------------------------------------

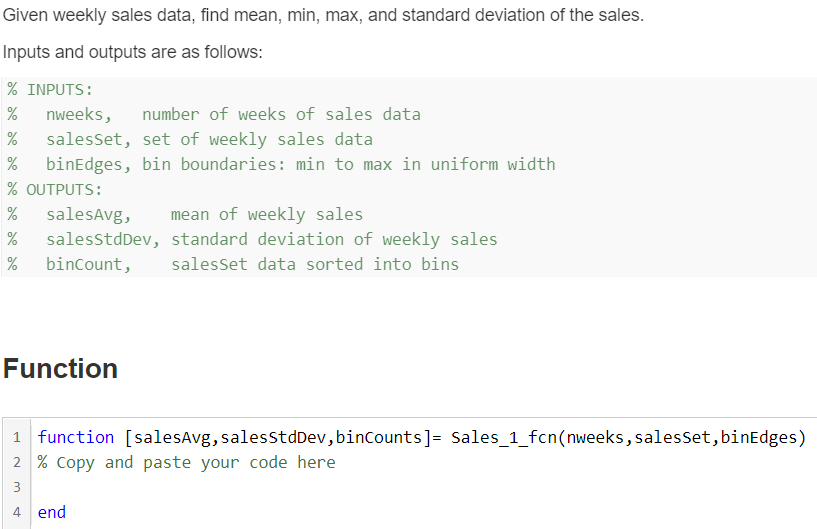
Given weekly sales data, find mean, min, max, and standard deviation of the sales. Inputs and outputs are as follows: % INPUTS: % nweeks, number of weeks of sales data % salesset, set of weekly sales data % binEdges, bin boundaries: min to max in uniform width % OUTPUTS: % salesAvg, mean of weekly sales % salesStdDev, standard deviation of weekly sales % binCount, salesset data sorted into bins Function 1 function [salesAvg, salesStdDev, binCounts]= Sales_1_fcn(nweeks, salesset, binEdges) 2 % Copy and paste your code here 4 end Given weekly sales data, find mean, min, max, and standard deviation of the sales. Inputs and outputs are as follows: % INPUTS: % nweeks, number of weeks of sales data % salesset, set of weekly sales data % binEdges, bin boundaries: min to max in uniform width % OUTPUTS: % salesAvg, mean of weekly sales % salesStdDev, standard deviation of weekly sales % binCount, salesset data sorted into bins Function 1 function [salesAvg, salesStdDev, binCounts]= Sales_1_fcn(nweeks, salesset, binEdges) 2 % Copy and paste your code here 4 end