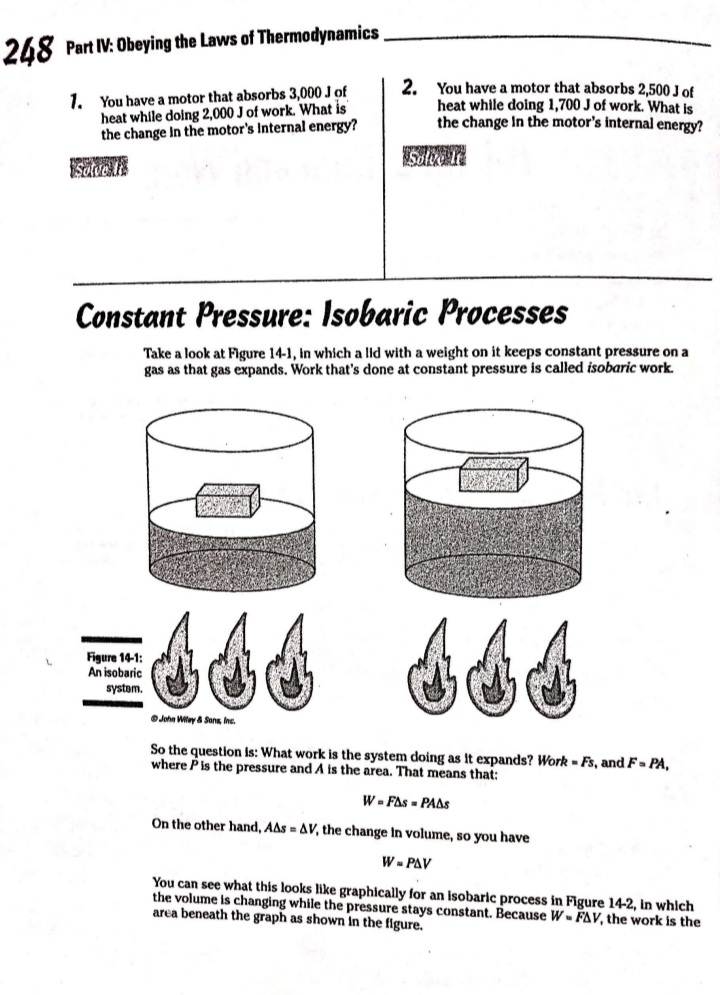
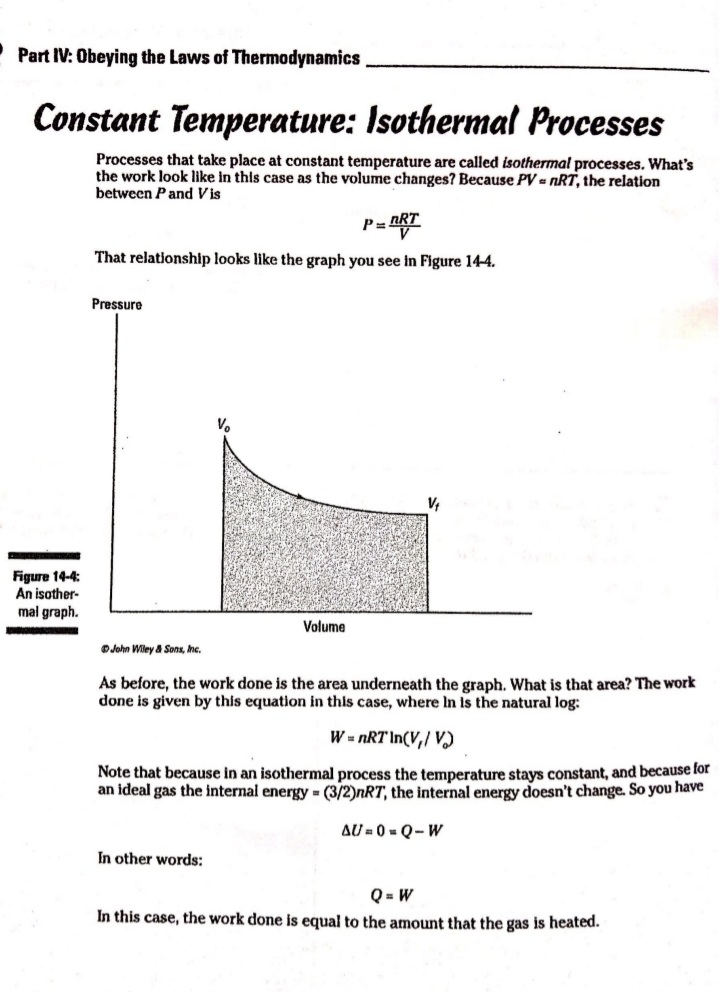
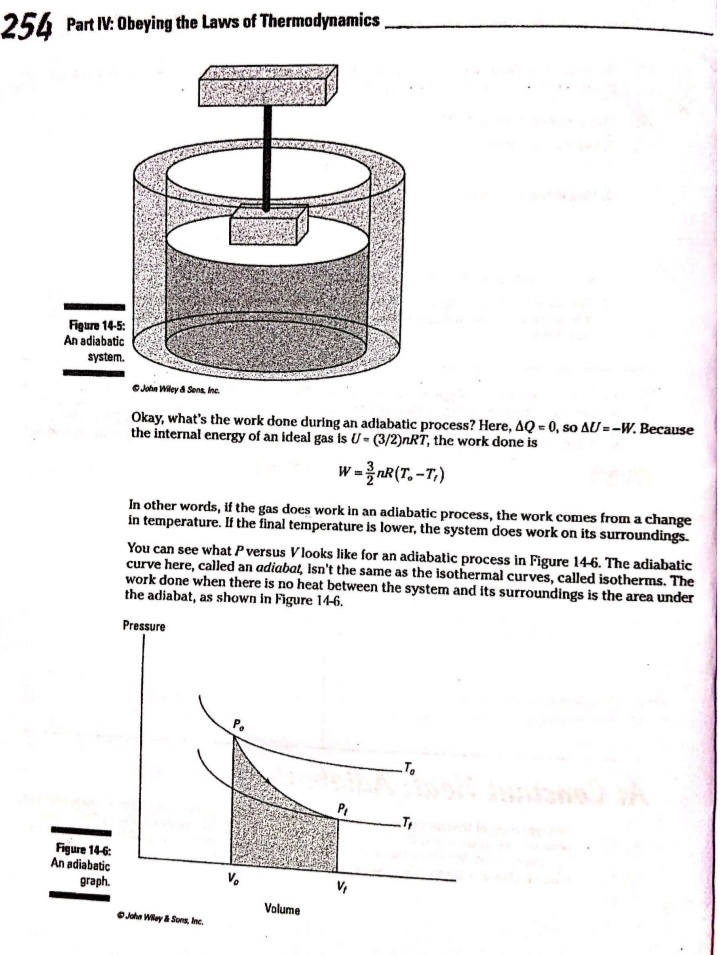
Chapter 14 All about Heat and Work In This Chapter Understanding the laws of thermodynamics Working with isobaric processes Handling isochoric processes Calculating isothermal processes his chapter is all about the laws of thermodynamics. Those laws describe all kinds of heat processes. You also discover how to handle heat processes where pressure is constant, or volume is constant, or temperature is constant. The First Law of Thermodynamics The first law of thermodynamics says that energy is conserved. The Internal energy in a system, U., changes to a final value U, when heat Q is absorbed or released by the system and the system does work Won its surroundings, or the surroundings do work Won the system, such that: U,-U. - AU - Q-W The value Q is positive when the system absorbs heat and negative when the system releases heat. The quantity Wis positive when the system does work on its surroundings and negative when the surroundings do work on the system. This law is useful because it says that total energy - Internal energy plus heat -is conserved. O. Say that a motor does 1,000 J of work on 2. The motor also releases 3,000 J of heat Its surroundings while releasing 3,000 J while doing its work, so the Internal of heat. By how much does its Internal energy of the system decreases by an energy change? additional 3,000 J. Think of negative values of work and heat as energy A. The correct answer is -4,000 J. flowing out of the system, making the 1. You know the motor does 1,000 J of total change of Internal energy this: work on its surroundings, so you know AU = -1,000 -3,000 - -4,000 J Its Internal energy decreases by 1,000 J.248 Part IV: Obeying the Laws of Thermodynamics 2. You have a motor that absorbs 2,500 J of 7. You have a motor that absorbs 3,000 J of heat while doing 1,700 J of work. What Is heat while doing 2,000 J of work. What is the change In the motor's internal energy? the change In the motor's Internal energy? Constant Pressure: Isobaric Processes Take a look at Figure 14-1, in which a lid with a weight on it keeps constant pressure on a gas as that gas expands. Work that's done at constant pressure is called isobaric work. Figure 14-1: An isobaric system. . John Wifey & Sons, Inc. So the question is: What work is the system doing as it expands? Work = Fs, and F = PA, where P is the pressure and A is the area. That means that: W = FAs = PAAs On the other hand, AAs = AV, the change In volume, so you have W = PAV You can see what this looks like graphically for an isobaric process in Figure 14-2, In which the volume is changing while the pressure stays constant. Because W . FAV, the work is the area beneath the graph as shown in the figure.Chapter 14: All about H 3/14 . . Pressure Figure 14-2: An isobaric graph. Volume John Wiley & Song, Inc. APLE You have 60.0 mr of an ideal gas at 200.0 Pa 2. Plug in the numbers: and heat the gas until it expands to a volume of 120 m . How much work did W - P. AV the gas do? (200.0 Pa) (120 m3- 60 m ) - 12,000 J A. The correct answer is 12,000 J. The gas did 12,000 J of work as it 1. Use this equation: expanded under constant pressure. W =P. AV 3. You have 50.0 m' of an ideal gas at 1,000.0 Pa 4. You have 300.0 m of an ideal gas at 1,500.0 Pa and heat the gas until it expands to a volume and heat the gas until it expands to a volume of 300.0 m'. How much work did the gas do? of 900.0 m'. How much work did the gas do? Solve InPart IV: Obeying the Laws of Thermodynamics 5. You have 50.0 m of an ideal gas at 1,000.0 Pa, 6. You have 100.0 m' of an ideal gas at 300.0 Pa, and the gas expands, doing 3,000.0 J of work. and it expands, doing 6,000.0 J of work. What What is the final volume of the gas? is the final volume of the gas? Solve it Solve It Constant Volume: Isochoric Processes When an ideal gas's pressure increases at constant volume, how much work is done? Because W = PAV the answer is simple: No work is being done. This is called an isochoric process, and you can see a graph of what's happening in Figure 14-3. Pressure P Figure 14-3: An isochoric graph. Volume John Wiley & Sons, Inc.Chapter 14: All about Heat and Work 24 As you see in the figure, the pressure rises while the volume stays the same, so no work is actually being done. EXAMPLE You have 60.0 m' of an ideal gas at A. The correct answer is none. 200.0 Pa and heat the gas until its 1. Use this equation: pressure is 300.0 Pa at the same volume. How much work did the gas do? W = PAV 2. Because AV = 0, no work was done. This process is an isochoric process. 7. You have 50.0 m' of an ideal gas at 1,000.0 Pa 8. You have 300.0 m3 of an ideal gas at 1,500.0 Pa and heat the gas until it has a pressure of and heat the gas until it has a pressure of 3,000.0 Pa, still at the same volume. How 6,000.0 Pa. How much work did the gas do? much work did the gas do? Solve It Solve ItPart IV: Obeying the Laws of Thermodynamics Constant Temperature: Isothermal Processes Processes that take place at constant temperature are called isothermal processes. What's the work look like in this case as the volume changes? Because PV = nRT, the relation between P and Vis P = ART That relationship looks like the graph you see in Figure 14-4. Pressure Figure 14-4: An isother- mal graph. Volume D John Wiley & Sons, Inc. As before, the work done is the area underneath the graph. What is that area? The work done is given by this equation in this case, where In is the natural log: W = nRT In(V,/ V) Note that because in an isothermal process the temperature stays constant, and because for an ideal gas the internal energy = (3/2)RT, the internal energy doesn't change. So you have AU = 0 = Q-W In other words: Q = W In this case, the work done is equal to the amount that the gas is heated.Chapter 14: All about Heat and Work 253 Q. You have 1.0 mole of ideal gas at a constant temperature of 20"C, and you expand the gas from V. = 0.010 m' to V, = 0.020 m'. What work did the gas do in expanding? A. The correct answer is 1,700 J. 1. Use this equation: W - nRT In(V,/V) 2. Plug in the numbers: W = nRT In(V,/V) (1.0)(8.31)(273.15 + 20) In(0.020 / 0.010) = 1,690 J which rounds to 1,700 J with significant figures. 3. The work done by the gas was 1,700 J. The change in the internal energy of the gas Is 0 J, as It must be in Isothermal processes. Because Q = W, the amount the gas was heated is equal to 1,700 J. 9. You have 1.0 mole of ideal gas at a constant 10. You have 0.60 mole of ideal gas at a constant temperature of 30.0"C, and you expand the temperature of 25"C, and you expand the gas from V. = 2.0 m' to V, = 3.0 m'. What gas from V. = 1.0 m' to V, = 3.0 m'. What work did the gas do in expanding? heat was supplied to the gas In expanding? Solve it Solve it At Constant Heat: Adiabatic The last type of thermodynamic process is the adiabatic process, in which there is no heat between the system and its surroundings. Take a look at the system in Figure 14-5; every- thing Is surrounded by an insulating substance, so the system can't heat Its surroundings. When a change occurs, it's going to be an adiabatic change.254 Part IV: Obeying the Laws of Thermodynamics Figure 14-5: An adiabatic system. John Wiley & Sons, Inc. Okay, what's the work done during an adiabatic process? Here, AQ = 0, so AU =-W. Because the internal energy of an ideal gas is U- (3/2)nRT, the work done is W = nR (T. -T,) In other words, if the gas does work in an adiabatic process, the work comes from a change in temperature. If the final temperature is lower, the system does work on its surroundings. You can see what Pversus Vlooks like for an adiabatic process in Figure 14-6. The adiabatic curve here, called an adiabat, isn't the same as the isothermal curves, called isotherms. The work done when there is no heat between the system and its surroundings is the area under the adiabat, as shown in Figure 14-6. Pressure To Figure 14-6: An adiabatic Va graph. Volume John Whey & Sons, Inc.Chapter 14: All about Heat and Work 255 You can relate the Initial pressure and volume to the final pressure and volume In an adiabatic process this way: P.V ! = P, VI What's y? It's the ratio of the specific heat capacity of an ideal gas at constant pressure divided by the specific heat capacity of an ideal gas at constant volume, C /C, What are C, and C? That makes the ratio y this: So you can connect pressure and volume at any two points along an adlabat this way. PVSA = P,VSA These processes are adiabatic; there is no heat between the system and Its surroundings. You start with 3.0 L of gas at 1.0 atmosphere A. The correct answer is 0.31 atmosphere. and end up, after an adiabatic change, with 6.0 L of gas. What is the new pressure? 1. Use this equation: P.V S/3 2. Plug in the numbers: P, = PV SA (1.0) (3.0) 573 V. SA (6.0) - = 0.31 atmosphere 17. You start with 1.0 L of gas at 1.0 atmosphere 12. You start with 1.5 L of gas at 1.7 atmospheres and end up after an adiabatic change with and end up after an adiabatic change with 3.0 L of gas. What is the new pressure? 2.9 L of gas. What is the new pressure? Solve it Solve it256 Part IV: Obeying the Laws of Thermodynamics 14. You have 3.0 moles of Ideal gas that undergo 13. You have 1.0 mole of Ideal gas that under- an adiabatic change, going from 23 C to goes an adiabatic change, going from 69*C. What work was done on the gas? 30.0'C to 10.0"C. What work did the gas do? Solve It Solve It The Direction of Heat: The Second Law of Thermodynamics You may see physics problems related to the definition of the second law of thermodynamics, which says, If no work is involved, then heat will always be from the object at higher temperature to the object at lower temperature. CHAMPLE O. A red-hot horseshoe is placed on an A. The correct answer is into the anvil. anvil at room temperature. Which way does the heat go between these two The second law of thermodynamics tells objects? you that heat is from hotter objects to cooler ones, so the heat is from the red- hot horseshoe to the room-temperature anvil.Chapter 14: All about Heat and Work 257 Making Heat Work: Heat Engines You know how a steam engine works: Heated steam does the work. Physics makes a study of this process, and you can see what's going on diagrammatically In Figure 14-7. Heat Is supplied to a heat engine, which does work and sends its exhaust to a lower-temperature heat sink. (Often, the heat sink is just the surroundings of the heat engine, as is the case with steam engines.) Heat source Engine - Work Figure 14-7: A heat engine. Heat sink D John Miley & Sons, Inc. Say that the heat supplied to the engine is Q,, and the heat sent to the heat sink is Q (h and c stand for the hot and cold reservoirs of heat). In that case, you could say that the efficiency of the work engine in terms of turning heat into work is Work W Efficiency " Heat Input On So if all the input heat is converted to work, the efficiency is 1.0. If none of the input heat is converted to work, the efficiency is 0.0. Note that because total energy is conserved, the heat into the engine must equal the work done plus the heat sent to the heat sink, which means: Q1 - W + Q. That In turn means you can rewrite the efficiency In terms of just Q, and Q, this way: Efficiency = W _ 9-06. =1-2-58 Part IV: Obeying the Laws of Thermodynamics AMPLE 3. Use this equation: Your car Is powered by a heat engine and does 3.0 x 107 J of work getting you up a small hill. If the heat engine is 25 percent efficient, how much heat did 4. Solve for QE It use, and how much did it exhaust? Q, - W= Q A. The correct answer is 1.2 x 10* J, 0.9 x 10# J. 5. Plug in the numbers: 1. Use this equation: Qn - W = 1.2 x 10# J-3.0 x 107 J Efficiency = Ox _ W 3.0x 10' J =0.25 = 0.9 x 108 J = Q So the output heat was 0.9 x 10# J. 2. Solve for OF: 0.25 Q, = 3.0x10'_ _1.2x10' J So the Input heat was 1.2 x 108 J. 15. A car running on a heat engine does 7.0 x 107 J of work. If the heat engine is 16. A car running using a heat engine does 26 percent efficient, how much heat did it 3.9 x 107 J of work. If the heat engine is use, and how much did it exhaust? 29 percent efficient, how much heat did it use, and how much did it exhaust? Solve It Solve ItChapter 14: All about Heat and Work 25 17. A 63 percent efficient heat engine does 18. An 87 percent efficient heat engine does 3.8 x 1010 J of work. How much heat did it 4.5 x 10"% J of work. How much heat did it use, use, and how much did it exhaust? and how much did it exhaust? Solve to Solve It 79. A heat engine does 4.6 x 10' J of work when 20. A heat engine does 8.1 x 107 J of work when supplied 8.9 x 107 J. What is its efficiency? supplied 10.9 x 107 J. What is its efficiency? Solve It Solve It50 Part IV: Obeying the Laws of Thermodynamics Maximum Efficiency: Carnot Heat Engines An engineer named Sadi Carnot figured out that the maximum possible efficiency of a heat engine is this: Efficiency = 1-7 The temperatures T, and T, are the temperatures of the heat source and heat sink, respectively, measured in Kelvin. That efficiency is the best a heat engine can get, assuming that no irreversible losses of energy occur due to friction or other causes. When you have a heat engine that does the best a heat engine can do, you have a Carnot engine, and the preceding equation is the expression for its efficiency. EXAMPLE Q. The heat source for a Carnot engine is at A. The correct answer is 21 percent. 100"C, and the heat sink is at 20"C. What is the engine's efficiency? 1. Use this equation: Efficiency = 1-7 2. Plug In the numbers: Efficiency = 1-- =1- (273.15+20) (273.15 +100) =21% 21. The heat source for a Carnot engine is at 22. The heat source for a Carnot engine is at 87"C, and the heat sink is at 49"C. What is 67"C, and the heat sink is at 29"C. What Is the engine's efficiency? the engine's efficiency? Solve it Solve It The Third Law of Thermodynamics This chapter finishes with the third law of thermodynamics, which says You cannot reach absolute zero through any process which uses a finite number of steps. In other words, you can get closer and closer to absolute zero step by step, but you can't actually reach it. This fact has been demonstrated in practice. Physicists have been able to approach absolute zero until they're just a fraction of a degree away, but no one has been able to reach it