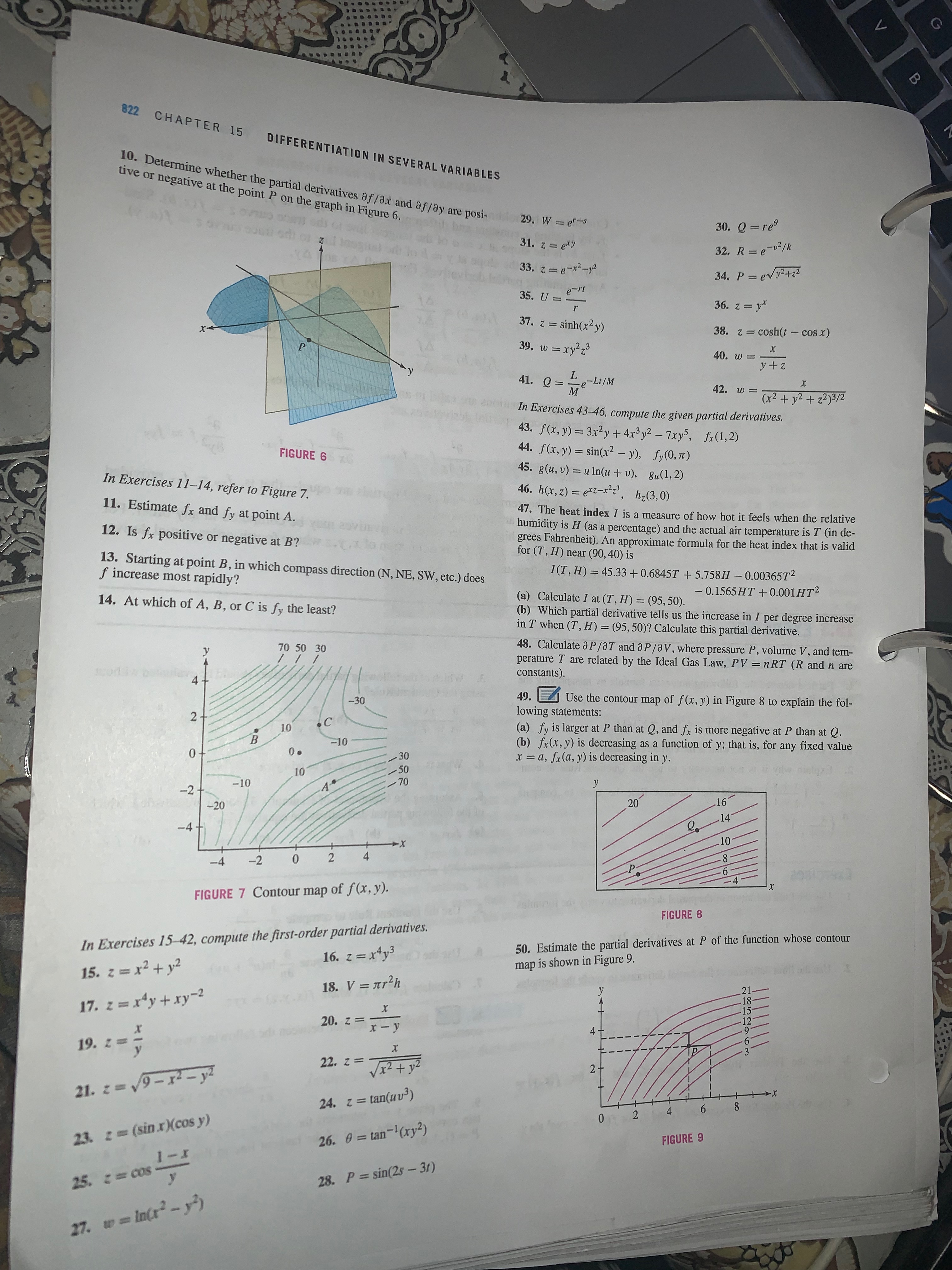
CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 10. Determine whether the partial derivatives af /ax and af/dy are posi- tive or negative at the point P on the graph in Figure 6. 29 . W = erts 30. Q = re 31. z = exy 32. R = e - v2/ k 33. z = e-x2-y2 34. P = evy2+22 35. U = en 36. z = yx 37. z = sinh(x2y) 38. z = cosh(t - cos x) 39. w = xyzz3 40. W = - y + z 41. Q =L Me-LIIM 42. W = ( x 2 + 1 2 + 2 2 ) 3 / 2 In Exercises 43-46, compute the given partial derivatives. 43 . f ( x , y ) = 3 x 2 y + 4x3 y 2 - 7xys, fx ( 1 , 2 ) FIGURE 6 44 . f ( x , y ) = sin ( x2 - y ), fy ( 0, It ) 45. 8 (u, v) = uIn(u + v), gu(1, 2 ) In Exercises 11-14, refer to Figure 7. 46. h(x, z) = exz-x273, hz (3, 0) 11. Estimate fx and fy at point A. 47. The heat index I is a measure of how hot it feels when the relative humidity is H (as a percentage) and the actual air temperature is T (in de- 12. Is fx positive or negative at B? grees Fahrenheit). An approximate formula for the heat index that is valid for (T, H) near (90, 40) is 13. Starting at point B, in which compass direction (N, NE, SW, etc.) does f increase most rapidly? I(T, H) = 45.33 + 0.68457 + 5.758H - 0.0036572 14. At which of A, B, or C is fy the least? (a) Calculate I at (T, H) = (95, 50). - 0.1565HT + 0.001 HT2 (b) Which partial derivative tells us the increase in I per degree increase in T when (T, H) = (95, 50)? Calculate this partial derivative. 70 50 30 48. Calculate @P /aT and a P /aV, where pressure P, volume V, and tem- perature T are related by the Ideal Gas Law, PV = nRT (R and n are constants ). 4 -30 49. Use the contour map of f(x, y) in Figure 8 to explain the fol- lowing statements: 2 10 (a) fy is larger at P than at Q, and fr is more negative at P than at Q. -10 (b) fx(x, y) is decreasing as a function of y; that is, for any fixed value 0 - - 30 x = a, fx(a, y) is decreasing in y -50 70 -10 20 -20 -4 -2 0 FIGURE 7 Contour map of f (x, y). FIGURE 8 In Exercises 15-42, compute the first-order partial derivatives. 50. Estimate the partial derivatives at P of the function whose contour 16. z = x4y3 map is shown in Figure 9. 15. z = x2 + 12 18. V = arch 17. z = xay + xy-2 20. z =_ 4+ 19. 2 = 22. z = Vx2 + y 2 - 21. z = 19-12 - y2 24. z = tan(uvs) 0 23. z = (sin .x)cos y) 26. 0 = tan -'(xy2) FIGURE 9 I -x 25. ) - x In(y?). 1xx(2.3) north. The angle D between magnetic north and true north is called the magnetic declination. Use Figure 10 to determine which of the following statements is true: 58. 8(x, y) -xe *7, gay(-3.2) (a) an 59. Compute fxyxzy for ay aD ay B (b) 3D aD f ( x. y. z) = Note that the horizontal axis increases from right to left because of the way ay 20 longitude is measured. y sin(xz) sin(x + 2) + (x+ z)tiny+xu(2+ Hint: Use a well-chosen order of differentiation on each term. 60. Let 50 N Magnetic Declination for the U.S. f ( x, y, 1, U) = 32 + In(2+ 12) What is the fastest way to show that fuexyou(x, y, u, v) = 0 for all (x, y, u, U)? 40ON In Exercises 61-68, compute the derivative indicated. A 61. f(u, v) = cos(u + v2), funv 30 N 62. 8 (x, y, z) = x4y z, gxxyz 63. F(r, s, 1 ) = 1($2 + 12 ), Fist 120.W 110 W 100 W 90.W 80W 64. u(x, 1) = 1-1/2e-(x2/41), Uxx FIGURE 10 Contour interval 10. 65. F(0, u, v) = sinh(uv + 02), Fund 52. Refer to Table 1. 66. R(u, v, W) = 7 , Ruvu -ut w ' (a) Using difference quotients, approximate ap/aT and ap/aS at the points (S, T) = (30, 2), (32, 6), and (35, 10). 67. 8 (x, y, z) = Vx2+>2+ z2, gxyz (b) For fixed salinity S = 32, determine whether the quotients Ap/ AT 68. u(x, t) = sech (x - t), uxxx are increasing or decreasing as T increases. What can you conclude about the sign of a2p/aT2 and the concavity of p as a function of T? 69. Find a function such that a 1 91 = 2xy and = x2. TABLE 1 Seawater Density p as a Function of Temperature gnon 70. Prove that there does not exist any function f(x, y) such that T and Salinity S I = xy and = x2. Hint: Consider Clairaut's Theorem. ax ay TS 30 31 32 33 34 35 36 22.75 23.51 24.27 25.07 25.82 26.6 27.36 71. Assume that fry and fyx are continuous and that fyxx exists. Show 12 that fryx also exists and that fyxx = fxyx. 10 23.07 23.85 24.62 25.42 26.17 26.99 27.73 8 23.36 24.15 24.93 25.73 26.5 27.28 29.09 72. Show that u(x, t) = sin(nx) e-" satisfies the heat equation for any constant n: 6 23.62 24.44 25.22 26 26.77 27.55 28.35 au 4 23.85 24.62 25.42 26.23 27 27.8 28.61 3 at ax 2 2 24 8 25.61 26.38 27.18 28.01 28.78 73. Find all values of A and B such that f (x, t) = eAx+Bi satisfies Eq. (3). 24.11 24.92 25.72 26.5 27.34 28.12 28.91 74. The function In Exercises 53-58, compute the derivatives indicated. f ( x, t ) = -e-x2 / 4t 2 2 f 53. f (x, y) = 3x2y - 6xy4, arz and ay 2 describes the temperature profile along a metal rod at time t > 0 when a burst of heat is applied at the origin (see Example 11). A small bug sit- 2 28 ting on the rod at distance x from the origin feels the temperature rise and 54. 8 (x, y) = _ y' ax dy fall as heat diffuses through the bar. Show that the bug feels the maximum temperature at time t = 7x2. u 55. h(u, v) = hou(u, v) In Exercises 75-78, the Laplace operator A is defined by u + 40 Af = fxx + fyy. A function u(x, y) satisfying the Laplace equation Au = 0 is called harmonic. 56. h(x, y) = In(x +y' ), hxy (x, y)
