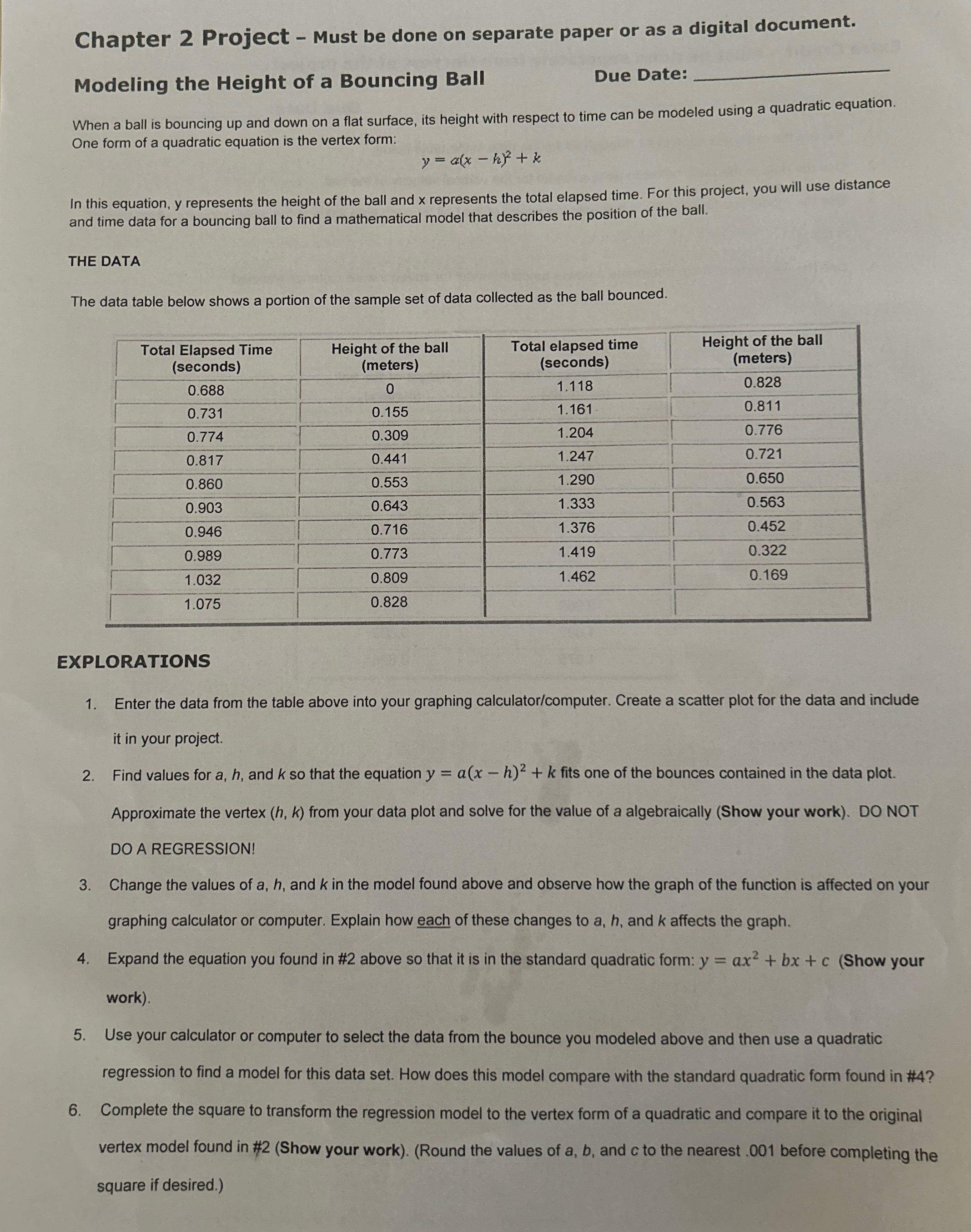
Chapter 2 Project - Must be done on separate paper or as a digital document. Modeling the Height of a Bouncing Ball Due Date: When a ball is bouncing up and down on a flat surface, its height with respect to time can be modeled using a quadratic equation. One form of a quadratic equation is the vertex form: y = a(x - 1) + * In this equation, y represents the height of the ball and x represents the total elapsed time. For this project, you will use distance and time data for a bouncing ball to find a mathematical model that describes the position of the ball. THE DATA The data table below shows a portion of the sample set of data collected as the ball bounced. Total Elapsed Time Height of the ball Total elapsed time Height of the ball (seconds) (meters) seconds) (meters) 0.688 1.118 0.828 0.731 0.155 1.161 0.811 0.774 0.30 1.204 0.776 0.817 0.441 1.247 0.721 0.860 0.553 1.290 0.650 0.903 0.643 1.333 0.563 0.946 0.716 1.376 0.452 0.989 0.773 1.419 0.322 1.032 0.809 1.462 0. 169 1.075 0.828 EXPLORATIONS 1. Enter the data from the table above into your graphing calculator/computer. Create a scatter plot for the data and include it in your project. 2. Find values for a, h, and k so that the equation y = a(x - h) + k fits one of the bounces contained in the data plot. Approximate the vertex (h, k) from your data plot and solve for the value of a algebraically (Show your work). DO NOT DO A REGRESSION! 3. Change the values of a, h, and k in the model found above and observe how the graph of the function is affected on your graphing calculator or computer. Explain how each of these changes to a, h, and k affects the graph. 4 . Expand the equation you found in #2 above so that it is in the standard quadratic form: y = ax + bx + c (Show your work). 5. Use your calculator or computer to select the data from the bounce you modeled above and then use a quadratic regression to find a model for this data set. How does this model compare with the standard quadratic form found in #4? 6. Complete the square to transform the regression model to the vertex form of a quadratic and compare it to the original vertex model found in #2 (Show your work). (Round the values of a, b, and c to the nearest .001 before completing the square if desired.)