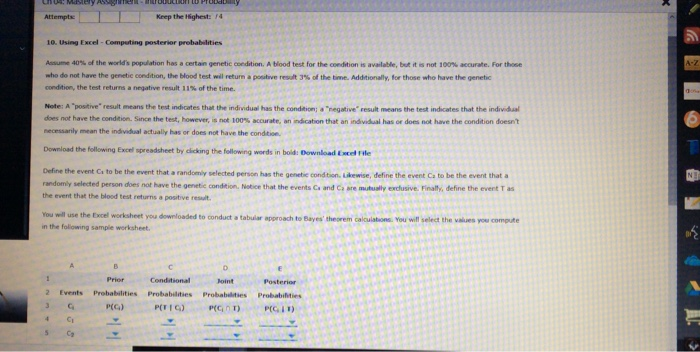
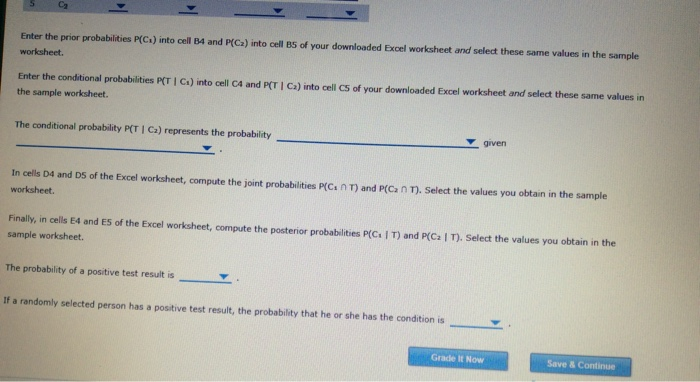
Chd4: Mastery AssgTR /4 Attempts Keep the Highest: 10. Using Excel-Computing posterior probabilities Assume 40 % of the world's population has a certain genetic coedition. A blood test for the coedition is available, but it is not 100 % accurate. For those A-Z who do not have the genetic condition, the blood test will return a positive result 3% of the time. Additionally,, for those who have the genetic condition, the test returns a nengative result 11 % of the time. Note: A "positive" result means the test indicates that the individual has the condition; a "negative" result means the test indicates that the individaal does not have the condition. Since the test, however, is not 100 % accurate, an indication that an individual has or does not have the condition doesn't necessarily mean the individual actually has or does not have the condition. Download the following Excel spreadsheet by cicking the following words in boid: Download Excel File Define the event Cs to be the event that a randomly selected person has the genetie condition. Likewise, define the event Ca to be the event that a randomly selected person does not have the genetic condition, Notice that the events Ca and Ca are mutually exclusive. Finally, define the event T as N the event that the blood test returns a positive result. You will use the Excel worksheet you downloaded to conduct a tabular approach to Bayes' theorem calcuiatons You will select the values you compute in the following sample worksheet B Prior Conditional Joint Posterior Events Probabilities Probabilities Probabilities Probabilities PIG) CT C) P(C T PIGI Ce Ca Enter the prior probabilities P(C) into cell B4 and P(Ca) into cell B5 of your downloaded Excel worksheet and select these same values in the sample worksheet. Enter the conditional probabilities P(T | Ca) into cell C4 and P(T I Ca) into cell CS of your downloaded Excel worksheet and select these same values in the sample worksheet. The conditional probability P(T I Ca) represents the probability given In cells D4 and DS of the Excel worksheet, compute the joint probabilities P(Cs n T) and P(Ca n T). Select the values you obtain in the sample worksheet. Finally, in cells E4 and E5 of the Excel worksheet, compute the posterior probabilities P(Cs I T) and P(C2 | T). Select the values you obtain in the sample worksheet. The probability of a positive test result is If a randomly selected person has a positive test result, the probability that he or she has the condition is Grade It Now Save & Continue Chd4: Mastery AssgTR /4 Attempts Keep the Highest: 10. Using Excel-Computing posterior probabilities Assume 40 % of the world's population has a certain genetic coedition. A blood test for the coedition is available, but it is not 100 % accurate. For those A-Z who do not have the genetic condition, the blood test will return a positive result 3% of the time. Additionally,, for those who have the genetic condition, the test returns a nengative result 11 % of the time. Note: A "positive" result means the test indicates that the individual has the condition; a "negative" result means the test indicates that the individaal does not have the condition. Since the test, however, is not 100 % accurate, an indication that an individual has or does not have the condition doesn't necessarily mean the individual actually has or does not have the condition. Download the following Excel spreadsheet by cicking the following words in boid: Download Excel File Define the event Cs to be the event that a randomly selected person has the genetie condition. Likewise, define the event Ca to be the event that a randomly selected person does not have the genetic condition, Notice that the events Ca and Ca are mutually exclusive. Finally, define the event T as N the event that the blood test returns a positive result. You will use the Excel worksheet you downloaded to conduct a tabular approach to Bayes' theorem calcuiatons You will select the values you compute in the following sample worksheet B Prior Conditional Joint Posterior Events Probabilities Probabilities Probabilities Probabilities PIG) CT C) P(C T PIGI Ce Ca Enter the prior probabilities P(C) into cell B4 and P(Ca) into cell B5 of your downloaded Excel worksheet and select these same values in the sample worksheet. Enter the conditional probabilities P(T | Ca) into cell C4 and P(T I Ca) into cell CS of your downloaded Excel worksheet and select these same values in the sample worksheet. The conditional probability P(T I Ca) represents the probability given In cells D4 and DS of the Excel worksheet, compute the joint probabilities P(Cs n T) and P(Ca n T). Select the values you obtain in the sample worksheet. Finally, in cells E4 and E5 of the Excel worksheet, compute the posterior probabilities P(Cs I T) and P(C2 | T). Select the values you obtain in the sample worksheet. The probability of a positive test result is If a randomly selected person has a positive test result, the probability that he or she has the condition is Grade It Now Save & Continue