class Node: def __init__(self, value): self.value = value self.next = None def __str__(self): return "Node({})".format(self.value)

__repr__ = __str__

class Stack: ''' >>> x=Stack() >>> x.pop() >>> x.push(2) >>> x.push(4) >>> x.push(6) >>> x Top:Node(6) Stack: 6 4 2 >>> x.pop() 6 >>> x Top:Node(4) Stack: 4 2 >>> len(x) 2 >>> x.peek() 4 ''' def __init__(self): self.top = None def __str__(self): temp=self.top out=[] while temp: out.append(str(temp.value)) temp=temp.next out=' '.join(out) return ('Top:{} Stack: {}'.format(self.top,out))

__repr__=__str__

def isEmpty(self): if self.top is None: return True return False

def __len__(self): count = 0 temp = self.top while temp: count += 1 temp = temp.next return count

def push(self,value): if self.top is None: self.top = Node(value) else: new_node = Node(value) new_node.next = self.top self.top = new_node

def pop(self): if self.top is None: return None else: popped = self.top.value self.top = self.top.next return popped

def peek(self): return self.top.value

class Calculator: def __init__(self): self.__expr = None

@property def getExpr(self): return self.__expr

def setExpr(self, new_expr): if isinstance(new_expr, str): self.__expr=new_expr else: print('setExpr error: Invalid expression') return None

def _isNumber(self, txt): ''' >>> x=Calculator() >>> x._isNumber(' 2.560 ') True >>> x._isNumber('7 56') False >>> x._isNumber('2.56p') False ''' # YOUR CODE STARTS HERE

def _getPostfix(self, txt): ''' Required: _getPostfix must create and use a Stack for expression processing >>> x=Calculator() >>> x._getPostfix('2 ^ 4') '2.0 4.0 ^' >>> x._getPostfix('2') '2.0' >>> x._getPostfix('2.1 * 5 + 3 ^ 2 + 1 + 4.45') '2.1 5.0 * 3.0 2.0 ^ + 1.0 + 4.45 +' >>> x._getPostfix('2 * 5.34 + 3 ^ 2 + 1 + 4') '2.0 5.34 * 3.0 2.0 ^ + 1.0 + 4.0 +' >>> x._getPostfix('2.1 * 5 + 3 ^ 2 + 1 + 4') '2.1 5.0 * 3.0 2.0 ^ + 1.0 + 4.0 +' >>> x._getPostfix('( 2.5 )') '2.5' >>> x._getPostfix ('( ( 2 ) )') '2.0' >>> x._getPostfix ('2 * ( ( 5 + -3 ) ^ 2 + ( 1 + 4 ) )') '2.0 5.0 -3.0 + 2.0 ^ 1.0 4.0 + + *' >>> x._getPostfix ('( 2 * ( ( 5 + 3 ) ^ 2 + ( 1 + 4 ) ) )') '2.0 5.0 3.0 + 2.0 ^ 1.0 4.0 + + *' >>> x._getPostfix ('( ( 2 * ( ( 5 + 3 ) ^ 2 + ( 1 + 4 ) ) ) )') '2.0 5.0 3.0 + 2.0 ^ 1.0 4.0 + + *' >>> x._getPostfix('2 * ( -5 + 3 ) ^ 2 + ( 1 + 4 )') '2.0 -5.0 3.0 + 2.0 ^ * 1.0 4.0 + +'

# In invalid expressions, you might print an error message, but code must return None, adjust doctest accordingly # If you are veryfing the expression in calculate before passing to postfix, this cases are not necessary

>>> x._getPostfix('2 * 5 + 3 ^ + -2 + 1 + 4') >>> x._getPostfix('2 * 5 + 3 ^ - 2 + 1 + 4') >>> x._getPostfix('2 5') >>> x._getPostfix('25 +') >>> x._getPostfix(' 2 * ( 5 + 3 ) ^ 2 + ( 1 + 4 ') >>> x._getPostfix(' 2 * ( 5 + 3 ) ^ 2 + ) 1 + 4 (') >>> x._getPostfix('2 * 5% + 3 ^ + -2 + 1 + 4') '''

# YOUR CODE STARTS HERE postfixStack = Stack() # method must use postfixStack to compute the postfix expression

@property def calculate(self): ''' Required: calculate must call postfix calculate must create and use a Stack to compute the final result as shown in the video lecture >>> x=Calculator() >>> x.setExpr('4 + 3 - 2') >>> x.calculate 5.0 >>> x.setExpr('-2 + 3.5') >>> x.calculate 1.5 >>> x.setExpr('4 + 3.65 - 2 / 2') >>> x.calculate 6.65 >>> x.setExpr('23 / 12 - 223 + 5.25 * 4 * 3423') >>> x.calculate 71661.91666666667 >>> x.setExpr(' 2 - 3 * 4') >>> x.calculate -10.0 >>> x.setExpr('7 ^ 2 ^ 3') >>> x.calculate 5764801.0 >>> x.setExpr(' 3 * ( ( ( 10 - 2 * 3 ) ) )') >>> x.calculate 12.0 >>> x.setExpr('8 / 4 * ( 3 - 2.45 * ( 4 - 2 ^ 3 ) ) + 3') >>> x.calculate 28.6 >>> x.setExpr('2 * ( 4 + 2 * ( 5 - 3 ^ 2 ) + 1 ) + 4') >>> x.calculate -2.0 >>> x.setExpr(' 2.5 + 3 * ( 2 + ( 3.0 ) * ( 5 ^ 2 - 2 * 3 ^ ( 2 ) ) * ( 4 ) ) * ( 2 / 8 + 2 * ( 3 - 1 / 3 ) ) - 2 / 3 ^ 2') >>> x.calculate 1442.7777777777778

# In invalid expressions, you might print an error message, but code must return None, adjust doctest accordingly >>> x.setExpr(" 4 + + 3 + 2") >>> x.calculate >>> x.setExpr("4 3 + 2") >>> x.calculate >>> x.setExpr('( 2 ) * 10 - 3 * ( 2 - 3 * 2 ) )') >>> x.calculate >>> x.setExpr('( 2 ) * 10 - 3 * / ( 2 - 3 * 2 )') >>> x.calculate >>> x.setExpr(' ) 2 ( * 10 - 3 * ( 2 - 3 * 2 ) ') >>> x.calculate

# For extra credit only. If not attemped, these cases must return None >>> x.setExpr('( 3.5 ) ( 15 )') >>> x.calculate 52.5 >>> x.setExpr('3 ( 5 ) - 15 + 85 ( 12 )') >>> x.calculate 1020.0 >>> x.setExpr("( -2 / 6 ) + ( 5 ( ( 9.4 ) ) )") >>> x.calculate 46.666666666666664 '''

if not isinstance(self.__expr,str) or len(self.__expr)

calcStack = Stack() # method must use calcStack to compute the expression

# YOUR CODE STARTS HERE pass

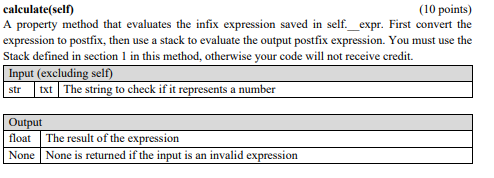
Section 2: The Calculator class (50 points) Implement a class that calculates mathematic expressions. The input passed to this Calculator is in infix notation, which gets converted to postfix internally, then the postfix expression is evaluated (we evaluate in postfix instead of infix because of how much simpler it is). More details about postfix can be found in the video lectures. This calculator should support numeric values, five arithmetic operators (+, - *, /,^), and parenthesis. Follow the PEMDAS order of operations (you can define precedence of operators with a dictionary). Note that exponentiation is ** in Python. You can assume that expressions will have tokens (operators, operands) separated by a single space. For the case of negative numbers, you can assume the negative sign will be prefixed to the number. The str.split() method can be helpful to isolate tokens. Expressions are considered invalid if they meet any of the following criteria: Contains unsupported operators 4 $ 5 Contains consecutive operators Has missing operands Has missing operators Has unbalanced parenthesis ) 4+ 5 ( or ( 4 + 5 ) ) Tries to do implied multiplication 3(5) instead of 3.5 Includes a space before a negative number 4* - 5 instead of 4.-5 Make sure to have proper encapsulation of your code by using proper variable scopes and writing other helper methods to generalize your code for processes such as string processing and input validation. Do not forget to document your code. As a suggestion, start by implementing your methods assuming the expressions are always valid, that way you have the logic implemented and you only need to work on validating the expressions. 4 * + 5 4 + 4 5 Attributes Type Name str expr Description The expression this calculator will evaluate Methods Type Name Description None setExpr(self, new_expr) Sets the expression for the calculator to evaluate getExpr(self) Getter method for the private expression attribute bool _isNumber(self, asring) Returns True if aSring can be converted to a float getPostfix(self, expr) Converts an expression from infix to postfix float calculate(self) Calculates the expression stored in this calculator str str setExpr(self, new_expr) Sets the expression for the calculator to evaluate. This method is already implemented for you. Input (excluding self) new_expr The new expression (in infix) for the calculator to evaluate str getExpr(self) Property method for getting the expression in the calculator. This method is already implemented for you. Output str The value stored in _expr _isNumber(self, txt) (5 points) Returns True if txt is a string that can be converted to a float, False otherwise. Note that float('4.56') returns 4.56 but float('4 56') raises an exception. A try/except block could be useful here. Input (excluding self) txt The string to check if it represents a number str Output bool True if txt can be successfully casted to a float, False otherwise _getPostfix(self, expr) (35 points) Converts an expression from infix to postfix. All numbers in the output must be represented as a float. You must use the Stack defined in section 1 in this method, otherwise your code will not receive credit. (Stack applications video lecture can be helpful here). Input (excluding self) expr The expression in infix form str Output str The expression in postfix form None None is returned if the input is an invalid expression calculate(self) (10 points) A property method that evaluates the infix expression saved in self._expr. First convert the expression to postfix, then use a stack to evaluate the output postfix expression. You must use the Stack defined in section 1 in this method, otherwise your code will not receive credit. Input (excluding self) txt The string to check if it represents a number str Output float The result of the expression None None is returned if the input is an invalid expression Section 2: The Calculator class (50 points) Implement a class that calculates mathematic expressions. The input passed to this Calculator is in infix notation, which gets converted to postfix internally, then the postfix expression is evaluated (we evaluate in postfix instead of infix because of how much simpler it is). More details about postfix can be found in the video lectures. This calculator should support numeric values, five arithmetic operators (+, - *, /,^), and parenthesis. Follow the PEMDAS order of operations (you can define precedence of operators with a dictionary). Note that exponentiation is ** in Python. You can assume that expressions will have tokens (operators, operands) separated by a single space. For the case of negative numbers, you can assume the negative sign will be prefixed to the number. The str.split() method can be helpful to isolate tokens. Expressions are considered invalid if they meet any of the following criteria: Contains unsupported operators 4 $ 5 Contains consecutive operators Has missing operands Has missing operators Has unbalanced parenthesis ) 4+ 5 ( or ( 4 + 5 ) ) Tries to do implied multiplication 3(5) instead of 3.5 Includes a space before a negative number 4* - 5 instead of 4.-5 Make sure to have proper encapsulation of your code by using proper variable scopes and writing other helper methods to generalize your code for processes such as string processing and input validation. Do not forget to document your code. As a suggestion, start by implementing your methods assuming the expressions are always valid, that way you have the logic implemented and you only need to work on validating the expressions. 4 * + 5 4 + 4 5 Attributes Type Name str expr Description The expression this calculator will evaluate Methods Type Name Description None setExpr(self, new_expr) Sets the expression for the calculator to evaluate getExpr(self) Getter method for the private expression attribute bool _isNumber(self, asring) Returns True if aSring can be converted to a float getPostfix(self, expr) Converts an expression from infix to postfix float calculate(self) Calculates the expression stored in this calculator str str setExpr(self, new_expr) Sets the expression for the calculator to evaluate. This method is already implemented for you. Input (excluding self) new_expr The new expression (in infix) for the calculator to evaluate str getExpr(self) Property method for getting the expression in the calculator. This method is already implemented for you. Output str The value stored in _expr _isNumber(self, txt) (5 points) Returns True if txt is a string that can be converted to a float, False otherwise. Note that float('4.56') returns 4.56 but float('4 56') raises an exception. A try/except block could be useful here. Input (excluding self) txt The string to check if it represents a number str Output bool True if txt can be successfully casted to a float, False otherwise _getPostfix(self, expr) (35 points) Converts an expression from infix to postfix. All numbers in the output must be represented as a float. You must use the Stack defined in section 1 in this method, otherwise your code will not receive credit. (Stack applications video lecture can be helpful here). Input (excluding self) expr The expression in infix form str Output str The expression in postfix form None None is returned if the input is an invalid expression calculate(self) (10 points) A property method that evaluates the infix expression saved in self._expr. First convert the expression to postfix, then use a stack to evaluate the output postfix expression. You must use the Stack defined in section 1 in this method, otherwise your code will not receive credit. Input (excluding self) txt The string to check if it represents a number str Output float The result of the expression None None is returned if the input is an invalid expression