


:Clearly solve the following problems.
On July 1, 2020, Bridgeport Aggregates Ltd. purchased 6% bonds having a maturity value of $65,000 for $67,331. The bonds provide the bondholders with a 5% yield. The bonds mature four years later, on July 1, 2024, with interest receivable June 30 and December 31 of each year. Bridgeport uses the effective interest method to allocate unamortized discount or premium. The bonds are accounted for using the FV-OCI model with recycling. Bridgeport has a calendar year end. The fair value of the bonds at December 31, 2020 and 2021, was $67,296 and $66,402, respectively. Assume fair value adjustments are recorded at year end only. Immediately after collecting interest on December 31, 2021, the bonds were sold for $66,402.
A. Prepare the journal entry at the date of the bond purchase (July 1, 2020).
B. Organize bond amortization schedule to December 31, 2021.
Schedule of Interest Revenue and Bond Premium Amortization
Effective-Interest Method
Date Cash Received Interest Revenue Premium Amortized Amortized Cost of Bonds
July 1, 2020 ? ? ? $
Dec. 31, 2020 $ $ $
June 30, 2021
Dec. 31, 2021
C. Prepare the entries and year-end entries from December 31, 2020, through to the collection of interest on December 31, 2021.
Date
Account Titles and Explanation
Debit
Credit
December 31, 2020June 30, 2021December 31, 2021
December 31, 2020June 30, 2021December 31, 2021
December 31, 2020June 30, 2021December 31, 2021
D. Following the three-step approach, prepare the journal entries for the sale of the bond on December 31, 2021. Include the reclassification of unrealized gains and losses to net income
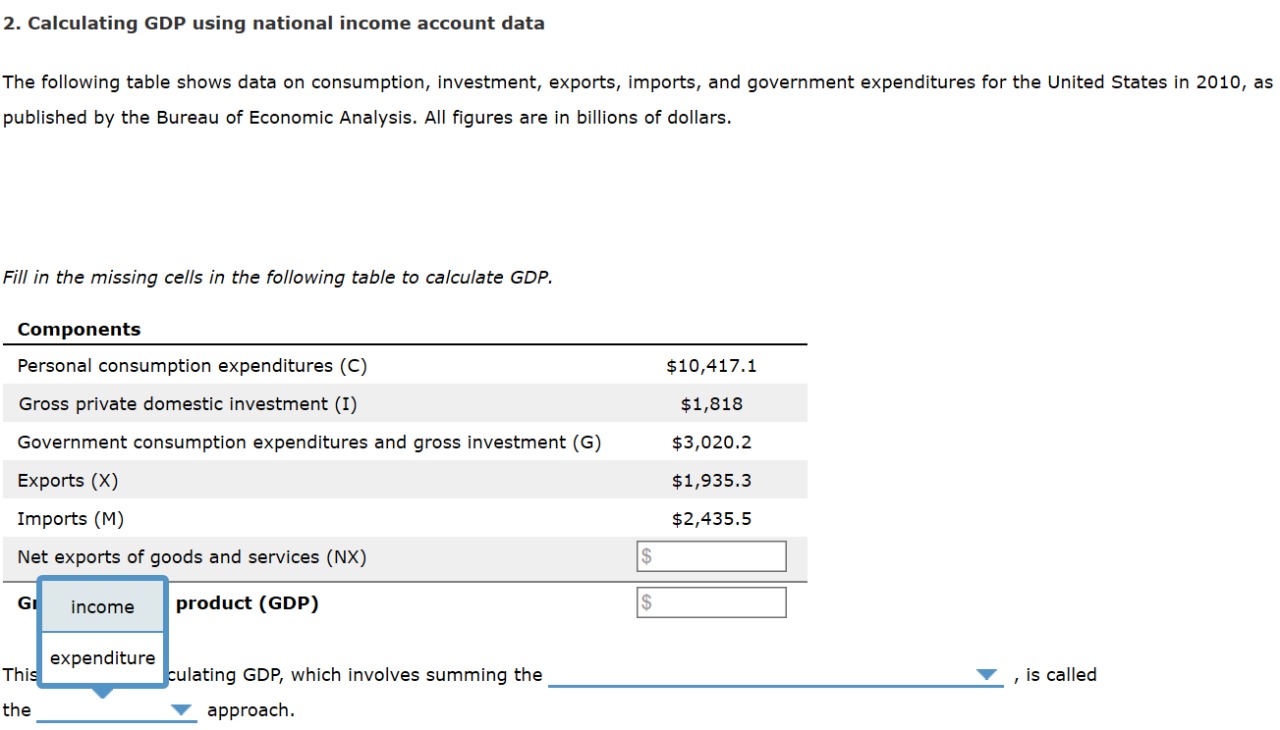
4. Two firms compete to sell a good. Total costs of the two firms respectively satisfy Ci(qi) = 2q1 and Co(q) = q;. The total output produced in the economy is Q = q1 + 92. The inverse demand for the total output produced by the two firms in this market satisfies P(Q) = 10-20 if Q5 0 if Q>5 Remember that the inverse demand curve identifies the highest price for which all the units supplied to the market are purchased. (a) First assume that firms compete on quantities. Find the Cournot equilibrium output at the two firms, the equilibrium price, and the profits at each of the two firms. (20 marks) (b) Then suppose that the two firms form a cartel. Find the cartel price and the output produced at the two firms? Compare your results with part (a). Does the cartel make higher profits than the two firms in part (a)? Does it produce more output on aggregate? (15 marks) (c) Finally assume that firms choose their output taking prices as given. Find the perfect competition price and the output produced at the two firms? Again, compare your results with parts (a) and (b). (14 marks)Since the materials may be a bit difficult, this first question on the Solow model is meant to walk you through it as a review. The Solow model begins with a constant-returns production function, Y = F(K. L). From this production function, we derive the per-worker version of it: y = f(k). where y = Y/L is the output per worker and k = K/L is the capital per worker. In this transformation, we assume that f (4) = F(k, 1). Since labor L is assumed to be fixed, 4 =0. Using the relation Ay AY AL L we conclude that the growth rate of output per worker is the same as the growth rate of total output. We are interested in how capital accumulation relates to economic growth. We need the following equation to describe the dynamics of capital, the so-called law of motion of k: Ak = i-6k, where & is investment per worker and & is the depreciation rate of capital. We focus our analysis on the steady states where capital per worker is constant, i.e., Ak = 0. (a) State the condition for steady state. In a steady state, what are the growth rates of output per worker and total output? (b) Show in a graph with production function, investment function, and depreciation the steady-state level of capital per worker, k*, and output per worker, y". (c) There is a change in climate in Country A so that the depreciation rate of capital increases from o to 8. Show in a graph how this would affect the steady-state level of capital. (d) Suppose that labor is now growing at the rate of n so that 4% = n. State the condition for steady state. In a steady state, what are the growth rates of output per worker and total output?Consider the general Solow growth model. Suppose production function at time f is described as: Y, = K, (AL,) I- where Y, is aggregate output, K, is aggregate capital stock, L, is total population or labour force and A, is technical progress enters in the production function, as labour-augmenting technology (also known as the effectiveness of labour). Suppose At= (1+g)A, and Le=(1+n)L, and the capital accumulation is given as: K = K,J - K, = SY, - OK,. A) Derive the per effective worker form production function. B) Define the balanced growth path. Using above growth model to drive the growth rates of Y, K. y=Y/L, k=K/L, y = /AL : and k = at the BGP. C) Use the above general Solow growth model to derive the law of motion equation. D) Drive the steady state values for output, capital and consumption per effective worker i.e. J*, k * and C *. E) Assume the values of parameters given as: s = 0.20, g = 0.02, n = 0.01, 8 = 0.05 and a =0.25 What is the value of k * and y *? Draw a diagram to show steady values. F) Use the above general Solow model to derive the golden rule saving rate. Use part (E) to calculate golden rule saving rate (SGR) and golden rule capital per effective worker value in the steady state i.e. kop *. Draw a diagram to explain the results in this part using appropriate labels of the curves. G) Using (E) and (F), what happens to the saving rate s=0.20 when it is compared with SCR? H) Derive the labour share of income from the above given production function. What are the values of labour and capital shares of income (no calculation required)?2. Calculating GDP using national income account data The following table shows data on consumption, Investment. exports, Imports, and government expenditures for the Unltecl States In 201.0, as published by the Bureau of Economic Analysis. All gures are in billions of dollars. Hi: in the missing cells in the following table to calculate GDP. components Personal consumption expenditures (C) $10,417.1 Gross private domestic Investment (I) $1,818 Government consumption expenditures and gross investment (G) $3,020.2 Exports (X) 51,9353 Imports (M) $2,435.5 Net exports of goods and services (NX) mm) expendlture ulating GDP, which involves summing the V , is called the V approach














