codes from file eval_exp.py and eval_exp_tests.py are given below

CODES ARE IN PYTHON PROGRAMMING LANGUAGE

please correct the codes according to the requirements and instructions from the picture, my test cases are failing

exp_eval.py does importing from a file called array_stack and it has been given at the very bottom incase you need it for reference

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

#exp_eval.py

from __future__ import annotations

#from array_stack import ArrayStack, empty_stack, push, pop, peek, is_empty, size

from array_stack import *

# NOTE: You'll probably need to import some things from array_stack.

def postfix_eval(input_string: str) -> float:

"""Evaluate the given RPN expression.

Args:

input_string: an RPN expression

Returns:

The result of the expression evaluation

Raises:

ValueError: if the input is not well-formed

ZeroDivisionError: if the input would cause division by zero

"""

# Split the input string into tokens

tokens = input_string.split()

# Initialize an empty stack

stack = ArrayStack.empty_stack()

# Process the expression from left to right

for token in tokens:

if token.isdigit():

# If the token is a number, push it onto the stack

ArrayStack.push(stack, float(token))

elif token in "+-*/":

# If the token is an operator, pop the required number of values from the stack

try:

op2 = ArrayStack.pop(stack)

op1 = ArrayStack.pop(stack)

except IndexError:

raise ValueError("insufficient operands")

# Perform the operation

if token == "+":

result = op1 + op2

elif token == "-":

result = op1 - op2

elif token == "*":

result = op1 * op2

elif token == "/":

if op2 == 0:

raise ZeroDivisionError("division by zero")

result = op1 / op2

# Push the result back onto the stack

ArrayStack.push(stack, result)

else:

# If the token is neither a valid operand nor a valid operator

raise ValueError("invalid token")

# Return the last value remaining on the stack

if ArrayStack.size(stack) != 1:

raise ValueError("too many operands")

return ArrayStack.pop(stack)

def infix_to_postfix(input_string: str) -> str:

"""Convert the given infix string to RPN.

Args:

input_string: an infix expression

Returns:

The equivalent expression in RPN

"""

operator_stack = ArrayStack()

operand_stack = ArrayStack()

tokens = input_string.split()

for token in tokens:

if token.isdigit():

ArrayStack.push(operand_stack, token)

elif token in "+-*/":

while (not ArrayStack.is_empty(operator_stack)) and (ArrayStack.peek(operator_stack) in "+-*/") and (precedence(ArrayStack.peek(operator_stack)) >= precedence(token)):

ArrayStack.push(operand_stack, ArrayStack.pop(operator_stack))

ArrayStack.push(operator_stack, token)

else:

raise ValueError("Invalid token")

while not ArrayStack.is_empty(operator_stack):

ArrayStack.push(operand_stack, ArrayStack.pop(operator_stack))

postfix_expression = " ".join(list(reversed([str(x) for x in operand_stack.array if x is not None])))

return postfix_expression

def precedence(operator: str) -> int:

if operator in "+-":

return 1

elif operator in "*/":

return 2

else:

raise ValueError("Invalid operator")

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

#eval_exp_tests.py

from __future__ import annotations

import unittest

from exp_eval import infix_to_postfix, postfix_eval

class Tests(unittest.TestCase):

def test_postfix_eval_01(self):

# NOTE: When testing for equality between values that could be

# floats, we should use assertAlmostEqual

self.assertAlmostEqual(postfix_eval("1 2 +"), 3)

def test_postfix_eval_02(self):

self.assertAlmostEqual(postfix_eval("1 2 -"), -1)

def test_postfix_eval_03(self):

self.assertAlmostEqual(postfix_eval("1 2 *"), 2)

def test_postfix_eval_04(self):

self.assertAlmostEqual(postfix_eval("1 2 /"), 0.5)

def test_postfix_eval_05(self):

self.assertAlmostEqual(postfix_eval("1 2 3 + *"), 5)

def test_postfix_eval_06(self):

self.assertAlmostEqual(postfix_eval("3 4 + 5 * 6 +"), 41)

def test_postfix_eval_07(self):

self.assertRaises(ValueError, postfix_eval, "1 2 + +")

def test_postfix_eval_08(self):

self.assertRaises(ZeroDivisionError, postfix_eval, "1 0 /")

def test_infix_to_postfix_01(self):

# NOTE: But for strings, we should stick with assertEqual

self.assertEqual(infix_to_postfix("1 + 2"), "1 2 +")

def test_infix_to_postfix_02(self):

self.assertEqual(infix_to_postfix("1 - 2"), "1 2 -")

def test_infix_to_postfix_03(self):

self.assertEqual(infix_to_postfix("1 * 2"), "1 2 *")

def test_infix_to_postfix_04(self):

self.assertEqual(infix_to_postfix("1 / 2"), "1 2 /")

def test_infix_to_postfix_05(self):

self.assertEqual(infix_to_postfix("1 + 2 * 3"), "1 2 3 * +")

def test_infix_to_postfix_06(self):

self.assertEqual(infix_to_postfix("3 + 4 * 5 + 6"), "3 4 5 * + 6 +")

def test_infix_to_postfix_07(self):

self.assertRaises(ValueError, infix_to_postfix, "1 + + 2")

if __name__ == "__main__":

unittest.main()

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

#array_stacks.py

from __future__ import annotations

from typing import Any

class ArrayStack:

def __init__(self) -> None:

self.capacity = 4

self.array: list[Any] = [None] * self.capacity

self.size = 0

"""Returns an empty stack."""

def empty_stack() -> ArrayStack:

return ArrayStack()

#def empty_stack(self) -> None:

#self.size = 0

"""Pushes an element to the top of the stack."""

def push(stack: ArrayStack, value: Any) -> None:

if stack.size == stack.capacity:

stack.capacity *= 2

new_array = [None] * stack.capacity

for i in range(stack.size):

new_array[i] = stack.array[i]

stack.array = new_array

stack.array[stack.size] = value

stack.size += 1

#def push(self, value: Any) -> None:

#if self.size == self.capacity:

#self.capacity *= 2

#new_array = [None] * self.capacity

#for i in range(self.size):

#new_array[i] = self.array[i]

#self.array = new_array

#self.array[self.size] = value

#self.size += 1

"""Removes and returns the element at the top of the stack."""

def pop(stack: ArrayStack) -> Any:

if stack.size == 0:

raise IndexError("pop from an empty stack")

value = stack.array[stack.size - 1]

stack.array[stack.size - 1] = None

stack.size -= 1

return value

"""Returns the element at the top of the stack."""

def peek(stack: ArrayStack) -> Any:

if stack.size == 0:

raise IndexError("peek from an empty stack")

return stack.array[stack.size - 1]

"""Returns True if the stack is empty, False otherwise."""

def is_empty(stack: ArrayStack) -> bool:

return stack.size == 0

"""Returns the number of elements in the stack."""

def size(stack: ArrayStack) -> int:

return stack.size

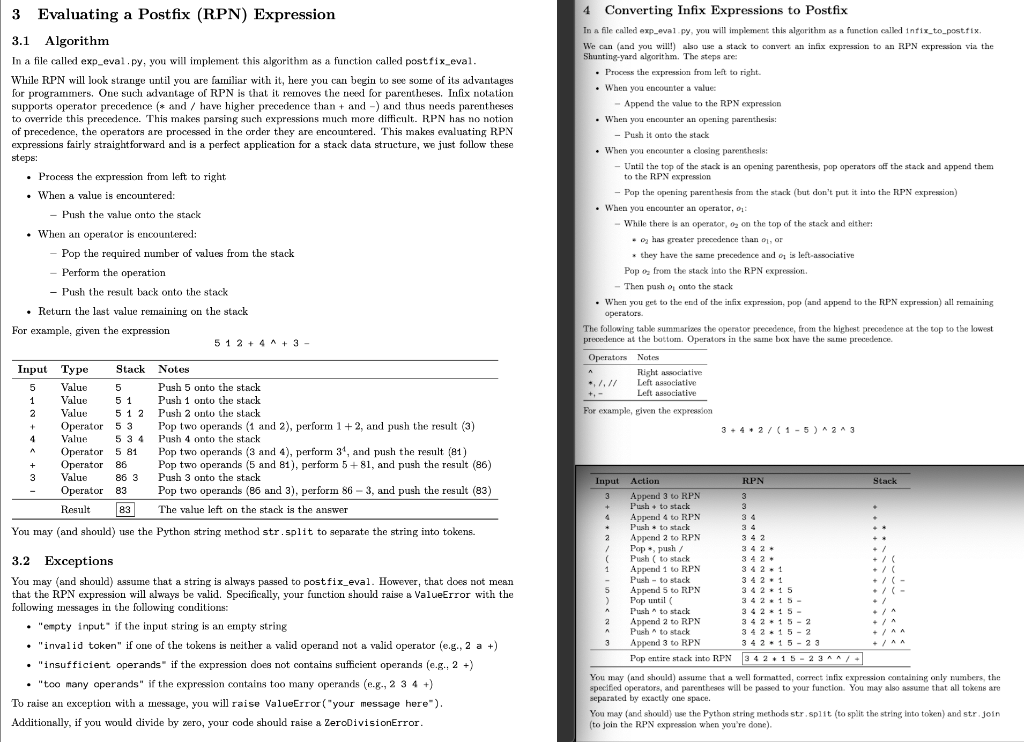
3 Evaluating a Postfix (RPN) Expression 4 Converting Infix Expressions to Postfix 3.1 Algorithm In a file called exp_eval py, you will implement this algorithm as a function calked intix_to_post.fix. In a file called exp_eval py, you will implement this algorithm as a function called postfix eeval. We can (and youl will) also use a stack to convert an infix expression to an RPN expression via the Shunting-yard algorithm. The steps are: While RPN will look strange until you are familiar with it, here you can begin to see some of its advantages - Process the expression from leet to right. for programmers. One such advantage of RPN is that it removes the neox for parentheses. Infix notation - When you encounter a value: supports operator precedence (* and / have higher precedence than + and ) and thus needs parentheses - Append the value to the RPN expression to override this precedence. This makes parsing such expressions much more difficult. R.PN has no notion - When you encounter an opening parenthesis: of precedence, the operators are processed in the order they are encountered. This makes evaluating RPN - Push it onto the stack expressions fairly straightforward and is a perfect application for a stack data structure, we just follow these steps: - When you encounter a clasing parenthesls: - Process the expression from left to right - Until the top of the stack is an opening parenthesis, pop opernators off the stack and append them - When a value is encountered: - Pop the opening parenthesis from the stark (bat don't put it into the R.PN expression) - Push the value onto the stack - When you eacouster an operator, 1: - When an operator is encountered; - While there is an operator, o2 on the top of the stack and either: - Pop the required number of values from the stack - o2 has greater precodence than o1, or - Perform the operation * they have the same precedence and q1 is leet-associative - Push the result back onto the stack Pop on from the stack into the RPN expresion. - Tben push o1 onto the stack - Return the last value remaining on the stack - When you get to the end of the infix expressian, pop (and append to the RPN expression) all remaining operators. For example, given the expression 512+4+3 The following table summarises the operator precedence, from the highest precedence at the top to the lawert precedence at the botiom. Operators in the same box have the same precedence. For example, given the expreasion 3+4+2/(15)23 You may (and should) wse the Python string method str.split to separate the string into tokens. 3.2 Exceptions You may (and should) assume that a string is always passed to postfin_eval. However, that does not mean that the RPN expression will always be valid. Specifically, your function should raise a ValueError with the following messages in the following conditions: - "empty input" if the input string is an empty string - "inval id token" if one of the tokens is neither a valid operand not a valid operator (e.g., 2 a +) - "insufficient operands" if the expression does not contains sufficient operands (e.g., 2 +) - "too many operands" if the expression contains too many operands (e.g., 234 +) To raise an exception with a message, you will raise ValueError ("your message here"). You may (and should) assume that a well formatted, correct infix cxpreseion containiag only numbers, the specifed operaters, and parentbeses will be passed to your function. You may also assume that all tobens are separated by exactly one space. Additionally, if you would divide by zero, your code should raise a ZerodivisionError. You may (and shoald) use the Python string methods str. split (to split the string into token) and ster. join (to join the RPN expreselon when you're done)