Question: Colligative Properties Freezing Point Depression in Aqueous Solutions OBJECTIVES - To measure the freezing points of the aqueous solutions of different ionic and molecular substances.




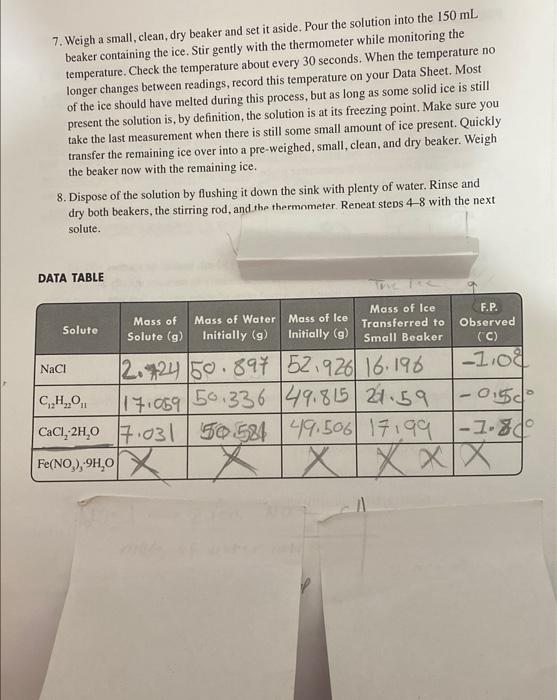
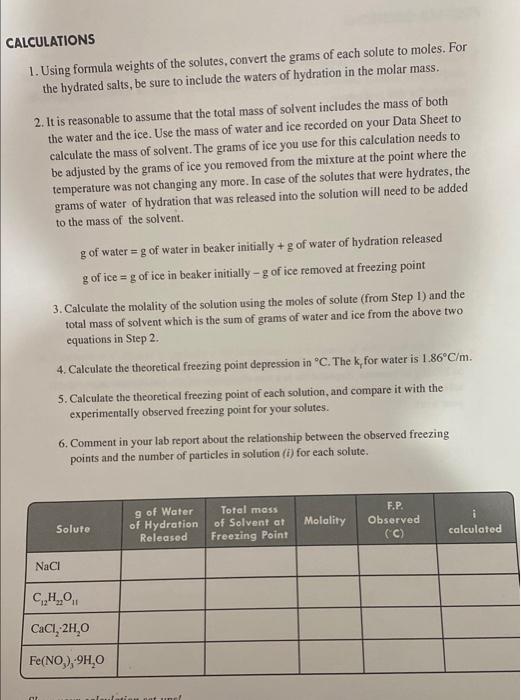
Colligative Properties Freezing Point Depression in Aqueous Solutions OBJECTIVES - To measure the freezing points of the aqueous solutions of different ionic and molecular substances. To estimate the value of van't Hoff's factor for the solutes from the measured freezing point depression they cause in water. BACKGROUND Colligative properties are properties of solutions that depend on the amount of the dissolved solute particles and not on their chemical identity. The most common colligative properties are boiling point elevation, freezing point depression, vapor pressure lowering, and osmotic pressure. By putting salt on icy sidewalks, the freezing point of water is decreased, so the ice melts. Mixing antifreeze with the water in your automobile radiator increases the boiling point of the water to prevent your radiator from boiling over in summer traffic. Adding salt or sugar when canning fruits or vegetables increases the osmotic pressure of the canning solution, which kills bacteria and prevents spoiling. In this lab you will explore freezing point depression by observing the change in the freezing point of water as various solutes are added. Colligative properties of solutions can be described using equations that take into account the properties of the solvent and the concentration of dissolved solute particles. The boiling points and freezing points of solvents depend on the intermolecular attractive forces between solvent molecules. Changes in these forces occur when the presence of a solute disrupts these interactions. Since the magnitude of intermolecular forces varies from solvent to solvent, the varying properties of the solvents are incorporated into the equations as a specific constant, k, for each solvent. For freezing point depression and boiling point elevation, these equations are: Tr=kqmTb=kbm where T1 and Tt are the changes in the freezing point and boiling point of the solution compared to pure solvent, Kf and kh are the freezing point depression and boiling point elevation constants for the solvent, and m is the concentration of solute in molality. Molality has the units 'moles of solute per kilogram of solvent', and is more useful for calculation of these colligative properties because, unlike molarity, it is independent of temperature. Thus, the unit for k is C/molality, or 9Cxkg/mol All solutes, however, are not created equal. Most water-soluble molecular substances, such as sucrose, C12H2O41, will remain as discrete solvated molecules when dissolved in water: C12H22Oi(s)H2OC12H22O11(aq) These substances are called non-electrolyles. Other solutes will dissociate, or come apart in solution to form ions. For example, sodium ctloride ( NaCl or "table salt") will dissociate into aqueous Nat and Cl : NaCl(s)H2OH2ONa(aq)+Cl(aq) For sodium chleeride, and many other salts, the dissociation or ionization process is essentially complete ( (1000 tionization) in aqueous solutions. Such substances are called strong electrolytes. Other substances, such as acetic acid, are weak electrolytes and will only partially ionines: some of the molecules will dissociate, but the majority remains intact: CH3COOH(aq)+H2OCH3COO(aq)+H3O(aq) Since the colligative properties af solutions depend on the concentration of dissolved solute particles, an additional factor is included in the colligative property equations to account for the formation of multiple particles a clectrolyles dissociate: Tr=ikrmT1=ikbm The additional factori is callod the viat't Hoff factor and corrects for the formation of multiple solute paricics when clectrobtes dissolve in solution. The following examples illust tate the dissolution of rome sthong electrolytes, and their respective i values: NaClNa++Cl2CaCl2Ca2+2Cl3FeO1Fel2+3Cl EXAMPLE Calculate the theoretical boiling point of a solution prepared by dissolving 25.0g of ethanol (C2H5OH) in 150.0mL of water. The kb for water is 0.52C/m. SOLUTION We start by calculating the molality of ethanol in the solution. From the formula of ethanol we obtain a MM=46.1g/mol. Assuming that the density of water is 1.00g/mL, the molality is determined as: 150gH2O25.0gC2H5OH46.1CC2H5OH1molC2H5OH=0.150kgH2O0.542molC2H5OH=3.62m Since ethanol is a molecular solute, the value of i=1. We can now calculate the boiling point elevation as: T=ikbm=(1)(0.52C/m)(3.62m)=1.88C Since the normal boiling point of water is 100.00C, the new boiling point of the solution is 100.00C+1.88C=101.88C. PROCEDURE 1. Obtain a thermometer, three 150mL beakers, a plastic weigh boat or weighing paper, a stirring rod, a large beaker of crushed ice, and some distilled water. 2. Prepare an ice bath by filling one of the 150 -mL beakers with crushed ice and about 50 mL of distilled water. Stir with a clean stirring rod. Check the temperature of the ice bath with your thermometer/thermometer probe. Record this temperature on your Data Sheet. If your thermometer does not read 0.0C tepeat this step carefully to avoid any possible contamination. This is your reference 0C measurement. If your thermometer still does not read 0.0C, you may have to correct for an error in subsequent measurements and/or calculations. 3. Weigh out 50g of distilled water in a clean, dry 150mL beaker. In another 150 -mL beaker, weigh out 50g of ice. While it is not necessary to measure exactly 50g of ice or water, it is important to record the actual mass of water and ice that you obtain to the nearest mg. Record these masses on your Data Sheet. Complete Steps 4-8 with each of the solutes listed in Step 4. 4. Weigh out the amount of your solute as indicated below, using a weighing dish or weighing paper. Record the identity and mass of your solute on the Data Sheet. NaCl(tablesalt)=2.9gC12H22O11(sucrose)=17.1gCaCl22H2O(calciumchloridedihydrate)=7.4gFe(NO3)39H2O(iron(III)nitratenonahydrate)=20.2g Again, you do not need to weigh out these exact masses, but you should record the actual mass obtained on your Data Sheet. 5. Transfer the weighed solid to the beaker containing the 50g of distilled water. Try to transfer the entire amount of the solid to the beaker, but don't try to rinse it in with any additional water. 6. Stir the solution in the beaker with a clean stirring rod until all the solid dissolves. Do not proceed to the next step until the solid has completely dissolved. 7. Weigh a small, clean, dry beaker and set it aside. Pour the solution into the 150mL beaker containing the ice. Stir gently with the thermometer while monitoring the temperature. Check the temperature about every 30 seconds. When the temperature no longer changes between readings, record this temperature on your Data Sheet. Most of the ice should have melted during this process, but as long as some solid ice is still present the solution is, by definition, the solution is at its freezing point. Make sure you take the last measurement when there is still some small amount of ice present. Quickly transfer the remaining ice over into a pre-weighed, small, clean, and dry beaker. Weigh the beaker now with the remaining ice. 8. Dispose of the solution by flushing it down the sink with plenty of water. Rinse and dry both beakers, the stirring rod, and the thermnmeter. Reneat steps 4-8 with the next solute. DATA TABLE ALCULATIONS 1. Using formula weights of the solutes, convert the grams of each solute to moles. For the hydrated salts, be sure to include the waters of hydration in the molar mass. 2. It is reasonable to assume that the total mass of solvent includes the mass of both the water and the ice. Use the mass of water and ice recorded on your Data Sheet to calculate the mass of solvent. The grams of ice you use for this calculation needs to be adjusted by the grams of ice you removed from the mixture at the point where the temperature was not changing any more. In case of the solutes that were hydrates, the grams of water of hydration that was released into the solution will need to be added to the mass of the solvent. g of water =g of water in beaker initially +g of water of hydration released g of ice =g of ice in beaker initially g of ice removed at freezing point 3. Calculate the molality of the solution using the moles of solute (from Step 1) and the total mass of solvent which is the sum of grams of water and ice from the above two equation in Step 2. 4. Calculate the theoretical freezing point depression in C. The k for water is 1.86C/m. 5. Calculate the theoretical freezing point of each solution, and compare it with the experimentally observed freezing point for your solutes. 6. Comment in your lab report about the relationship between the observed freezing points and the number of particles in solution (i) for each solute. Colligative Properties Freezing Point Depression in Aqueous Solutions OBJECTIVES - To measure the freezing points of the aqueous solutions of different ionic and molecular substances. To estimate the value of van't Hoff's factor for the solutes from the measured freezing point depression they cause in water. BACKGROUND Colligative properties are properties of solutions that depend on the amount of the dissolved solute particles and not on their chemical identity. The most common colligative properties are boiling point elevation, freezing point depression, vapor pressure lowering, and osmotic pressure. By putting salt on icy sidewalks, the freezing point of water is decreased, so the ice melts. Mixing antifreeze with the water in your automobile radiator increases the boiling point of the water to prevent your radiator from boiling over in summer traffic. Adding salt or sugar when canning fruits or vegetables increases the osmotic pressure of the canning solution, which kills bacteria and prevents spoiling. In this lab you will explore freezing point depression by observing the change in the freezing point of water as various solutes are added. Colligative properties of solutions can be described using equations that take into account the properties of the solvent and the concentration of dissolved solute particles. The boiling points and freezing points of solvents depend on the intermolecular attractive forces between solvent molecules. Changes in these forces occur when the presence of a solute disrupts these interactions. Since the magnitude of intermolecular forces varies from solvent to solvent, the varying properties of the solvents are incorporated into the equations as a specific constant, k, for each solvent. For freezing point depression and boiling point elevation, these equations are: Tr=kqmTb=kbm where T1 and Tt are the changes in the freezing point and boiling point of the solution compared to pure solvent, Kf and kh are the freezing point depression and boiling point elevation constants for the solvent, and m is the concentration of solute in molality. Molality has the units 'moles of solute per kilogram of solvent', and is more useful for calculation of these colligative properties because, unlike molarity, it is independent of temperature. Thus, the unit for k is C/molality, or 9Cxkg/mol All solutes, however, are not created equal. Most water-soluble molecular substances, such as sucrose, C12H2O41, will remain as discrete solvated molecules when dissolved in water: C12H22Oi(s)H2OC12H22O11(aq) These substances are called non-electrolyles. Other solutes will dissociate, or come apart in solution to form ions. For example, sodium ctloride ( NaCl or "table salt") will dissociate into aqueous Nat and Cl : NaCl(s)H2OH2ONa(aq)+Cl(aq) For sodium chleeride, and many other salts, the dissociation or ionization process is essentially complete ( (1000 tionization) in aqueous solutions. Such substances are called strong electrolytes. Other substances, such as acetic acid, are weak electrolytes and will only partially ionines: some of the molecules will dissociate, but the majority remains intact: CH3COOH(aq)+H2OCH3COO(aq)+H3O(aq) Since the colligative properties af solutions depend on the concentration of dissolved solute particles, an additional factor is included in the colligative property equations to account for the formation of multiple particles a clectrolyles dissociate: Tr=ikrmT1=ikbm The additional factori is callod the viat't Hoff factor and corrects for the formation of multiple solute paricics when clectrobtes dissolve in solution. The following examples illust tate the dissolution of rome sthong electrolytes, and their respective i values: NaClNa++Cl2CaCl2Ca2+2Cl3FeO1Fel2+3Cl EXAMPLE Calculate the theoretical boiling point of a solution prepared by dissolving 25.0g of ethanol (C2H5OH) in 150.0mL of water. The kb for water is 0.52C/m. SOLUTION We start by calculating the molality of ethanol in the solution. From the formula of ethanol we obtain a MM=46.1g/mol. Assuming that the density of water is 1.00g/mL, the molality is determined as: 150gH2O25.0gC2H5OH46.1CC2H5OH1molC2H5OH=0.150kgH2O0.542molC2H5OH=3.62m Since ethanol is a molecular solute, the value of i=1. We can now calculate the boiling point elevation as: T=ikbm=(1)(0.52C/m)(3.62m)=1.88C Since the normal boiling point of water is 100.00C, the new boiling point of the solution is 100.00C+1.88C=101.88C. PROCEDURE 1. Obtain a thermometer, three 150mL beakers, a plastic weigh boat or weighing paper, a stirring rod, a large beaker of crushed ice, and some distilled water. 2. Prepare an ice bath by filling one of the 150 -mL beakers with crushed ice and about 50 mL of distilled water. Stir with a clean stirring rod. Check the temperature of the ice bath with your thermometer/thermometer probe. Record this temperature on your Data Sheet. If your thermometer does not read 0.0C tepeat this step carefully to avoid any possible contamination. This is your reference 0C measurement. If your thermometer still does not read 0.0C, you may have to correct for an error in subsequent measurements and/or calculations. 3. Weigh out 50g of distilled water in a clean, dry 150mL beaker. In another 150 -mL beaker, weigh out 50g of ice. While it is not necessary to measure exactly 50g of ice or water, it is important to record the actual mass of water and ice that you obtain to the nearest mg. Record these masses on your Data Sheet. Complete Steps 4-8 with each of the solutes listed in Step 4. 4. Weigh out the amount of your solute as indicated below, using a weighing dish or weighing paper. Record the identity and mass of your solute on the Data Sheet. NaCl(tablesalt)=2.9gC12H22O11(sucrose)=17.1gCaCl22H2O(calciumchloridedihydrate)=7.4gFe(NO3)39H2O(iron(III)nitratenonahydrate)=20.2g Again, you do not need to weigh out these exact masses, but you should record the actual mass obtained on your Data Sheet. 5. Transfer the weighed solid to the beaker containing the 50g of distilled water. Try to transfer the entire amount of the solid to the beaker, but don't try to rinse it in with any additional water. 6. Stir the solution in the beaker with a clean stirring rod until all the solid dissolves. Do not proceed to the next step until the solid has completely dissolved. 7. Weigh a small, clean, dry beaker and set it aside. Pour the solution into the 150mL beaker containing the ice. Stir gently with the thermometer while monitoring the temperature. Check the temperature about every 30 seconds. When the temperature no longer changes between readings, record this temperature on your Data Sheet. Most of the ice should have melted during this process, but as long as some solid ice is still present the solution is, by definition, the solution is at its freezing point. Make sure you take the last measurement when there is still some small amount of ice present. Quickly transfer the remaining ice over into a pre-weighed, small, clean, and dry beaker. Weigh the beaker now with the remaining ice. 8. Dispose of the solution by flushing it down the sink with plenty of water. Rinse and dry both beakers, the stirring rod, and the thermnmeter. Reneat steps 4-8 with the next solute. DATA TABLE ALCULATIONS 1. Using formula weights of the solutes, convert the grams of each solute to moles. For the hydrated salts, be sure to include the waters of hydration in the molar mass. 2. It is reasonable to assume that the total mass of solvent includes the mass of both the water and the ice. Use the mass of water and ice recorded on your Data Sheet to calculate the mass of solvent. The grams of ice you use for this calculation needs to be adjusted by the grams of ice you removed from the mixture at the point where the temperature was not changing any more. In case of the solutes that were hydrates, the grams of water of hydration that was released into the solution will need to be added to the mass of the solvent. g of water =g of water in beaker initially +g of water of hydration released g of ice =g of ice in beaker initially g of ice removed at freezing point 3. Calculate the molality of the solution using the moles of solute (from Step 1) and the total mass of solvent which is the sum of grams of water and ice from the above two equation in Step 2. 4. Calculate the theoretical freezing point depression in C. The k for water is 1.86C/m. 5. Calculate the theoretical freezing point of each solution, and compare it with the experimentally observed freezing point for your solutes. 6. Comment in your lab report about the relationship between the observed freezing points and the number of particles in solution (i) for each solute
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


