complete all requirements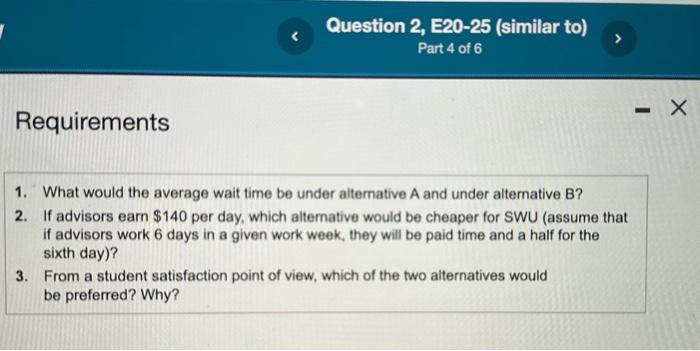

delete question since you were not able to answer it in the time frame and this is all tje info i have. no more help needed from you

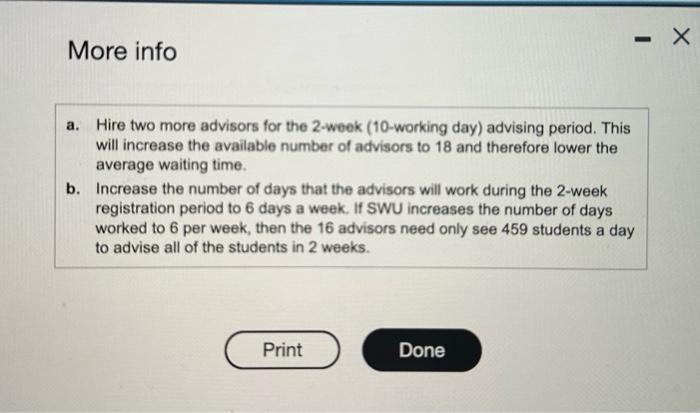
Requirements 1. What would the average wait time be under alternative A and under alternative B ? 2. If advisors earn $140 per day, which altemative would be cheaper for SWU (assume that if advisors work 6 days in a given work week, they will be paid time and a half for the sixth day)? 3. From a student satisfaction point of view, which of the two alternatives would be preferred? Why? More info a. Hire two more advisors for the 2-week (10-working day) advising period. This will increase the available number of advisors to 18 and therefore lower the average waiting time. b. Increase the number of days that the advisors will work during the 2 -week registration period to 6 days a week. If SWU increases the number of days worked to 6 per week, then the 16 advisors need only see 459 students a day to advise all of the students in 2 weeks. The regittration advisors mt a small wvstem university (SWU) help 5,500 students develop their dats schediles and mogster for elasses nach semneter, Each adkeor works for 10 hours a day dul the registration period. SWU currenth has 16 advisoes. While advising an individual student can taks anywhere from 2 to 30 minutes, it takes an average of 14 minutes per studert. Ouring the registration period, the 16 advisors see an average of 400 students a doy on a frst-como, frst-sorved basis. The head of the registraticn advisors at $ Wu has decided that the adviscre must Ginish their advising in 2 weeks (10 working days) and therelore must advise \$50 students a day. However, the average waiting time given a 14 -minule advising period will result in student complarts, wil redusing the average advising time to 13 minutes. SWU is considering two ahernatives: Begin by selecting the formula to calculate the wall time. (Abbreviations used: Ave w average; Hrs = hours, and Max = maxmum. (Ave students per day) ( (Time per stusent) 2 2 Max time evailablo - (Ave students per day Time per studenef) = Wat time Calculate the average wail tme under alternative A. (Enter the amounts in the same order as shown in the formuta. Rocnd the wait bime to wo docimal places.) minutes of wat time Calculate the everage wat Ime under allomateve B. (Enter the amounts in the same order as ahown in the formula. Fcund the wait time to two decimal places.) Requirement 2. If advisors earn $140 per day, which alternative would be cheeper for SWu (8ssume that if advisors work 6 drys in a gven work weok; they will be paid time and a haif for the sixith ding)? The total cost undet alternative A (el sWu hites two more edvisors for the 2 -week (10-wodkng day) advising poriod) Requirements 1. What would the average wait time be under alternative A and under alternative B ? 2. If advisors earn $140 per day, which altemative would be cheaper for SWU (assume that if advisors work 6 days in a given work week, they will be paid time and a half for the sixth day)? 3. From a student satisfaction point of view, which of the two alternatives would be preferred? Why? More info a. Hire two more advisors for the 2-week (10-working day) advising period. This will increase the available number of advisors to 18 and therefore lower the average waiting time. b. Increase the number of days that the advisors will work during the 2 -week registration period to 6 days a week. If SWU increases the number of days worked to 6 per week, then the 16 advisors need only see 459 students a day to advise all of the students in 2 weeks. The regittration advisors mt a small wvstem university (SWU) help 5,500 students develop their dats schediles and mogster for elasses nach semneter, Each adkeor works for 10 hours a day dul the registration period. SWU currenth has 16 advisoes. While advising an individual student can taks anywhere from 2 to 30 minutes, it takes an average of 14 minutes per studert. Ouring the registration period, the 16 advisors see an average of 400 students a doy on a frst-como, frst-sorved basis. The head of the registraticn advisors at $ Wu has decided that the adviscre must Ginish their advising in 2 weeks (10 working days) and therelore must advise \$50 students a day. However, the average waiting time given a 14 -minule advising period will result in student complarts, wil redusing the average advising time to 13 minutes. SWU is considering two ahernatives: Begin by selecting the formula to calculate the wall time. (Abbreviations used: Ave w average; Hrs = hours, and Max = maxmum. (Ave students per day) ( (Time per stusent) 2 2 Max time evailablo - (Ave students per day Time per studenef) = Wat time Calculate the average wail tme under alternative A. (Enter the amounts in the same order as shown in the formuta. Rocnd the wait bime to wo docimal places.) minutes of wat time Calculate the everage wat Ime under allomateve B. (Enter the amounts in the same order as ahown in the formula. Fcund the wait time to two decimal places.) Requirement 2. If advisors earn $140 per day, which alternative would be cheeper for SWu (8ssume that if advisors work 6 drys in a gven work weok; they will be paid time and a haif for the sixith ding)? The total cost undet alternative A (el sWu hites two more edvisors for the 2 -week (10-wodkng day) advising poriod)