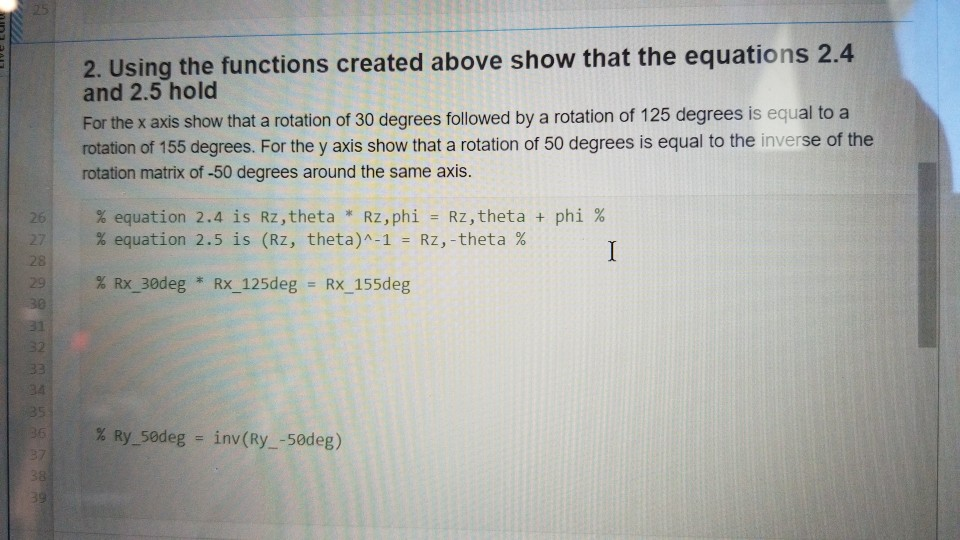
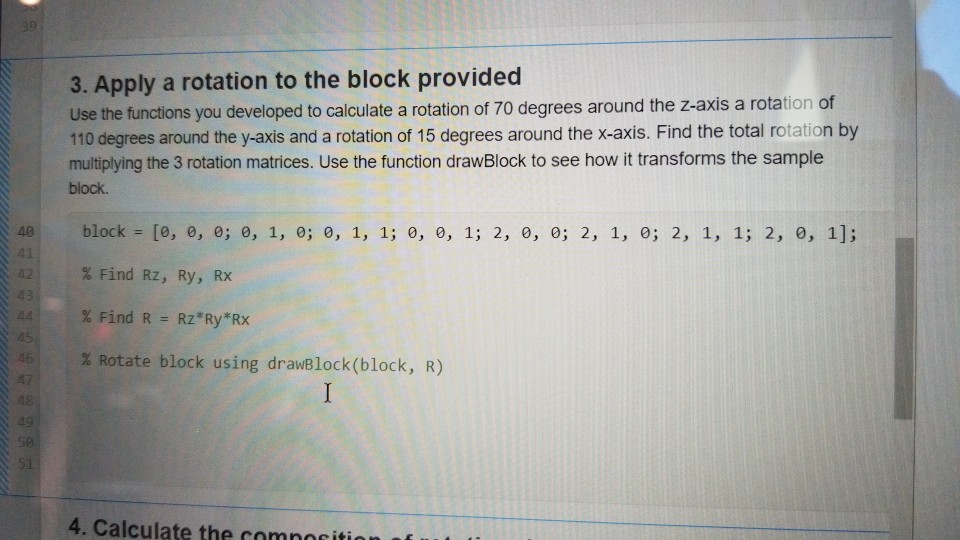
Complete following questions using matlab

1. Write two functions to provide the rotation matrix around the x and y axes Using the provided templates write 2 functions that will return the basic rotation matrix around the x and y axes as shown in equations 2.6 and 2.7 Use the provided templates getRotationX() and getRotation for x and y respectively. The input to your functions is an angle in degrees and the function should return the rotation matrix as a 3 by 3 matrix. See the getRotationZ() function for example. Test your functions' output by plotting the rotated coordinate system using the drawAxis function as shown below. Use a 30 degrees rotation for the X axis and 160 degrees for the Y axis clear: close all; clc; % Rotation around Z axis Rz = getRotationz (45); drawAxis (RZ); % Rotation around Y axis % Rotation around x axis 2. Using the functions created above show that the equations 2.4 and 2.5 hold For the x axis show that a rotation of 30 degrees followed by a rotation of 125 degrees is equal to a rotation of 155 degrees. For the y axis show that a rotation of 50 degrees is equal to the inverse of the rotation matrix of -50 degrees around the same axis. % equation 2.4 is Rz, theta * Rz, phi = Rz, theta + phi % % equation 2.5 is (Rz, theta)^-1 = Rz, -theta % 29 % Rx_30deg * Rx_125deg = Rx_155deg 20 361 37 % Ry_5deg = inv(Ry_-5deg) 3. Apply a rotation to the block provided Use the functions you developed to calculate a rotation of 70 degrees around the z-axis a rotation of 110 degrees around the y-axis and a rotation of 15 degrees around the x-axis. Find the total rotation by multiplying the 3 rotation matrices. Use the function drawBlock to see how it transforms the sample block. block = [0, 0, 0; 0, 1, 0; 0, 1, 1; 0, 0, 1; 2, 0, 0; 2, 1, 0; 2, 1, 1; 2, 0, 1]; % Find Rz, Ry, Rx % Find R = Rz*Ry*Rx % Rotate block using drawBlock (block, R) 4. Calculate the camne. Live Editor Curt 4. Calculate the composition of rotational transformations Following example 2.8 suppose R is defined by the following sequence of basic rotations in the specified order: 1. A rotation of 21 degrees around the current y-axis 2. A rotation of 14 degrees around the fixed Z-axis 3. A rotation of 35 degrees around the current Z-axis 4. A rotation of 72 degrees around the fixed x-axis 5. A rotation of 81 degrees around the fixed y-axis 6. A rotation of 46 degrees around the current x-axis % Use getRotationxo, getRotationy(), getRotationzo) to find the individual % rotation matrices % Find their composition R % Apply the rotation to the block by using drawBlock (block, R) 5. Find the Euler angles and the Axis/Angle representation of R Using the composition R you calculated in the previous problem find the correpsonding Euler angles using the ZYX sequence as well as the axis/angle representation. Use the function drawAxis() to see the axis of rotation of R % Use rotm2eul(R) to find the ZYX-Euler angles (The results are in radians % so you can use radadeg() to change them to degrees if you want) % Use [k, theta] = findAxisTheta(R) to find the axis k and angle theta % Use drawblock(block, R, k) to see the rotated block and its axis of % rotation has a par- products are zero. Thus the rotation matrix R m in this case, namely cose - sino 01 sino cose 0 0 0 1 (2.2) on Matrices ix given in Equation (2.2) is called a basic rotation matrix . In this case we find it useful to use the more descriptive ead of R to denote the matrix. It is easy to verify that the trix Re has the properties R..0 = 1 (2.3) R2,0R2,4 = R.,0+6 (2.4) mply (R.2) = R.- (2.5) basic rotation matrices representing rotations about the x and as (Problem 2-8) 1 0 0 R = 0 cos sin (2.6) 0 sino cos 0 cos 0 0 sine 1 Rye = 0 1 0 (2.7) - sin 8 0 cose] isfy properties analogous to Equations (2.3)-(2.5). 1. Write two functions to provide the rotation matrix around the x and y axes Using the provided templates write 2 functions that will return the basic rotation matrix around the x and y axes as shown in equations 2.6 and 2.7 Use the provided templates getRotationX() and getRotation for x and y respectively. The input to your functions is an angle in degrees and the function should return the rotation matrix as a 3 by 3 matrix. See the getRotationZ() function for example. Test your functions' output by plotting the rotated coordinate system using the drawAxis function as shown below. Use a 30 degrees rotation for the X axis and 160 degrees for the Y axis clear: close all; clc; % Rotation around Z axis Rz = getRotationz (45); drawAxis (RZ); % Rotation around Y axis % Rotation around x axis 2. Using the functions created above show that the equations 2.4 and 2.5 hold For the x axis show that a rotation of 30 degrees followed by a rotation of 125 degrees is equal to a rotation of 155 degrees. For the y axis show that a rotation of 50 degrees is equal to the inverse of the rotation matrix of -50 degrees around the same axis. % equation 2.4 is Rz, theta * Rz, phi = Rz, theta + phi % % equation 2.5 is (Rz, theta)^-1 = Rz, -theta % 29 % Rx_30deg * Rx_125deg = Rx_155deg 20 361 37 % Ry_5deg = inv(Ry_-5deg) 3. Apply a rotation to the block provided Use the functions you developed to calculate a rotation of 70 degrees around the z-axis a rotation of 110 degrees around the y-axis and a rotation of 15 degrees around the x-axis. Find the total rotation by multiplying the 3 rotation matrices. Use the function drawBlock to see how it transforms the sample block. block = [0, 0, 0; 0, 1, 0; 0, 1, 1; 0, 0, 1; 2, 0, 0; 2, 1, 0; 2, 1, 1; 2, 0, 1]; % Find Rz, Ry, Rx % Find R = Rz*Ry*Rx % Rotate block using drawBlock (block, R) 4. Calculate the camne. Live Editor Curt 4. Calculate the composition of rotational transformations Following example 2.8 suppose R is defined by the following sequence of basic rotations in the specified order: 1. A rotation of 21 degrees around the current y-axis 2. A rotation of 14 degrees around the fixed Z-axis 3. A rotation of 35 degrees around the current Z-axis 4. A rotation of 72 degrees around the fixed x-axis 5. A rotation of 81 degrees around the fixed y-axis 6. A rotation of 46 degrees around the current x-axis % Use getRotationxo, getRotationy(), getRotationzo) to find the individual % rotation matrices % Find their composition R % Apply the rotation to the block by using drawBlock (block, R) 5. Find the Euler angles and the Axis/Angle representation of R Using the composition R you calculated in the previous problem find the correpsonding Euler angles using the ZYX sequence as well as the axis/angle representation. Use the function drawAxis() to see the axis of rotation of R % Use rotm2eul(R) to find the ZYX-Euler angles (The results are in radians % so you can use radadeg() to change them to degrees if you want) % Use [k, theta] = findAxisTheta(R) to find the axis k and angle theta % Use drawblock(block, R, k) to see the rotated block and its axis of % rotation has a par- products are zero. Thus the rotation matrix R m in this case, namely cose - sino 01 sino cose 0 0 0 1 (2.2) on Matrices ix given in Equation (2.2) is called a basic rotation matrix . In this case we find it useful to use the more descriptive ead of R to denote the matrix. It is easy to verify that the trix Re has the properties R..0 = 1 (2.3) R2,0R2,4 = R.,0+6 (2.4) mply (R.2) = R.- (2.5) basic rotation matrices representing rotations about the x and as (Problem 2-8) 1 0 0 R = 0 cos sin (2.6) 0 sino cos 0 cos 0 0 sine 1 Rye = 0 1 0 (2.7) - sin 8 0 cose] isfy properties analogous to Equations (2.3)-(2.5)