complete this python code from the images and the comments in the code:
import matplotlib.pyplot as plt
PI = 3.141592653589793238 M= float(1.989e+30) #[kg] #weight of the sun G= float(6.67e-11) #[m3 kg-1 s-2] #Gravitational constant
def main(): print("\t\t\t Welcome to Keppler's Third Law Software") print("") #Calculate your own pi value #INSERT YOUR CODE HERE #create the lists for data #INSERT YOUR CODE HERE
#Read the data from the input file #INSERT YOUR CODE HERE
#Compute The third law of Kepler #The square of the orbital period T of a planet #is proportional to the cube of the semi-major axis #a of its orbit: #INSERT YOUR CODE HERE #Plot the law of Periods #INSERT YOUR CODE HERE
print("Bye!") ## # @param # @return # def plot(num, denom): #INSERT YOUR CODE HERE ## # @param planets,periods and distance # @return # def readFile(planets, periods, distance): ## # @param # @return # def pi(prec): #INSERT YOUR CODE HERE
## # @param # @return # def thirdLaw(planets,distance,periods,LHS, num, denom): #INSERT YOUR CODE HERE
main()


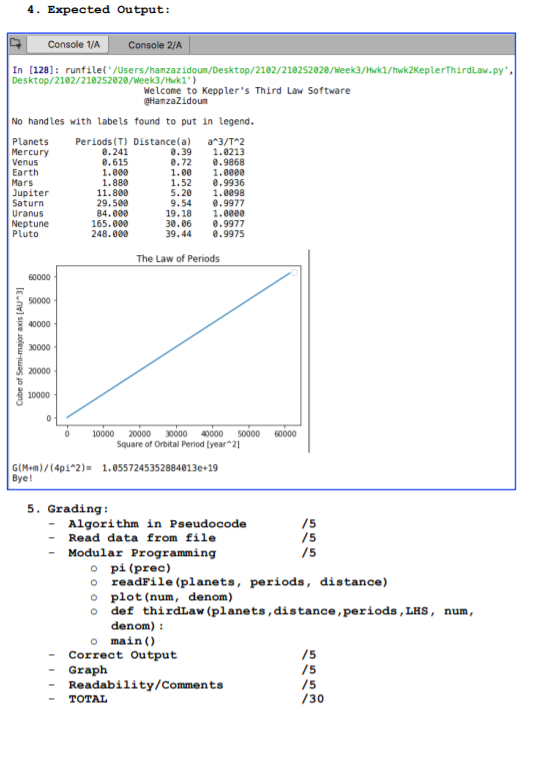
Apply the Development process to solve the following problem: Step 1: Define the problem: WHAT? Step 2: Specify the requirements Step 3: Design a solution/algorithm in Pseudo-code: HOW? Step 4: Implement the code Step 5: Test and verify Step 6: Repeat Steps 3 - 5 Step 7: Maintenance 1. The Problem: Planet In astronomy, Kepler's laws of planetary motion are three scientific laws describing the motion of planets around the Sun, published by Johannes Kepler between 1609 and 1619. Kepler and his theories were crucial in the better understanding of our solar system dynamics and as a springboard to newer theories that more accurately SUN approximate our planetary orbits. The usefulness of Kepler's laws extends to the motions of natural and artificial satellites, as well as to stellar systems and exo-planets. We are particularly interested in the Third law of Kepler. The third law of Kepler states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis a of its orbit: q? G(M + m) 42 where: Mis the mass of the Sun, M = 1.989e+30 kg, m is the mass of the planet, in solar mass G is the gravitational constant, G = 6.67e-11) (m kg s'] T is the orbital period (days) a is the elliptical semi-major axis, in Astronomical Units(AU). Kepler's Third Law implies that the period for a planet to orbit the Sun increases rapidly with the radius of its orbit. Thus we find that Mercury, the innermost planet, takes only 88 days to orbit the Sun. The earth takes 365 days, while Saturn requires 10,759 days to do the same. 2. Your Task: Your task is to develop a Python code to show that Kepler's law is correct! o Compute your own value for pi to the precision 10- 83279502854 Pi which is written as the Greek letter for p, or r-is the ratio of the circumference of 1415926535 any circle to the diameter of that circle. Regardless of the circle's size, this ratio will always equal pi. In decimal form, the value of pi is approximately 3.14. But pi is an irrational number, meaning that its decimal form neither ends nor becomes repetitive. To only 18 decimal places, pi is 3.141592653589793238. Calculate PI value using Gregory-Leibniz Series: 5820974944 2099986 29 82148 40 pi/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ... Write a function pi() to compute the value of pi using the Gregory-Leibniz Series. 3. The Data: Planet Mercury Venus Earth Mars Jupiter Saturn Uranus Neptune Pluto Period (yr) 0.241 0.615 1.00 1.88 11.8 29.5 84.0 165 248 Average Distance (AU) 0.39 0.72 1.00 1.52 5.20 9.54 19.18 30.06 39.44 NOTE: The average distance value is given in astronomical units where 1 a.u. is equal to the distance from the earth to the sun - 1.4957 x 1011 m. The orbital period is given in units of earth-years where 1 earth year is the time required for the earth to orbit the sun - 3.156 x 10 seconds. ) 4. Expected Output: Console 1/A Console 2/A 1/hw2KeplerThirdLaw.py", In [128]: runfilet/Users/hanzazidoun/Desktop/2162/21825202/week/ Desktop/212/210252020/week/Hki) Welcome to Keppler's Third Law Software HanzaZidoun No handles with labels found to put in legend. Planets Mercury Venus Earth Mars Jupiter Saturn Uranus Neptune Pluto Periods (T) Distance(a) 2.241 2.39 2.615 @.72 1.000 1.ee 1.888 1.52 11.800 5.20 29.500 9.54 84.000 19.18 165.000 30.06 248.000 39.44 a^3/T2 1.0213 e.9868 1.eeee 0.9936 1.2298 e.9977 1. eeee 0.9977 .9975 The Law of Periods 60000 50000 40000 Cube of Semi-major axis (AU"3] 20.000 20000 10000 20000 30000 40000 50000 Square of Orbital Period year21 60000 1.0557245352884013e-19 G(Men)/(4p1*2) Bye! 5. Grading: - Algorithm in Pseudocode - Read data from file - Modular Programming opi (prec) readrile (planets, periods, distance) plot (num, denom) def thirdLaw (planets, distance, periods, LHS, num, denom): main() Correct Output - Graph - Readability/Comments TOTAL Apply the Development process to solve the following problem: Step 1: Define the problem: WHAT? Step 2: Specify the requirements Step 3: Design a solution/algorithm in Pseudo-code: HOW? Step 4: Implement the code Step 5: Test and verify Step 6: Repeat Steps 3 - 5 Step 7: Maintenance 1. The Problem: Planet In astronomy, Kepler's laws of planetary motion are three scientific laws describing the motion of planets around the Sun, published by Johannes Kepler between 1609 and 1619. Kepler and his theories were crucial in the better understanding of our solar system dynamics and as a springboard to newer theories that more accurately SUN approximate our planetary orbits. The usefulness of Kepler's laws extends to the motions of natural and artificial satellites, as well as to stellar systems and exo-planets. We are particularly interested in the Third law of Kepler. The third law of Kepler states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis a of its orbit: q? G(M + m) 42 where: Mis the mass of the Sun, M = 1.989e+30 kg, m is the mass of the planet, in solar mass G is the gravitational constant, G = 6.67e-11) (m kg s'] T is the orbital period (days) a is the elliptical semi-major axis, in Astronomical Units(AU). Kepler's Third Law implies that the period for a planet to orbit the Sun increases rapidly with the radius of its orbit. Thus we find that Mercury, the innermost planet, takes only 88 days to orbit the Sun. The earth takes 365 days, while Saturn requires 10,759 days to do the same. 2. Your Task: Your task is to develop a Python code to show that Kepler's law is correct! o Compute your own value for pi to the precision 10- 83279502854 Pi which is written as the Greek letter for p, or r-is the ratio of the circumference of 1415926535 any circle to the diameter of that circle. Regardless of the circle's size, this ratio will always equal pi. In decimal form, the value of pi is approximately 3.14. But pi is an irrational number, meaning that its decimal form neither ends nor becomes repetitive. To only 18 decimal places, pi is 3.141592653589793238. Calculate PI value using Gregory-Leibniz Series: 5820974944 2099986 29 82148 40 pi/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ... Write a function pi() to compute the value of pi using the Gregory-Leibniz Series. 3. The Data: Planet Mercury Venus Earth Mars Jupiter Saturn Uranus Neptune Pluto Period (yr) 0.241 0.615 1.00 1.88 11.8 29.5 84.0 165 248 Average Distance (AU) 0.39 0.72 1.00 1.52 5.20 9.54 19.18 30.06 39.44 NOTE: The average distance value is given in astronomical units where 1 a.u. is equal to the distance from the earth to the sun - 1.4957 x 1011 m. The orbital period is given in units of earth-years where 1 earth year is the time required for the earth to orbit the sun - 3.156 x 10 seconds. ) 4. Expected Output: Console 1/A Console 2/A 1/hw2KeplerThirdLaw.py", In [128]: runfilet/Users/hanzazidoun/Desktop/2162/21825202/week/ Desktop/212/210252020/week/Hki) Welcome to Keppler's Third Law Software HanzaZidoun No handles with labels found to put in legend. Planets Mercury Venus Earth Mars Jupiter Saturn Uranus Neptune Pluto Periods (T) Distance(a) 2.241 2.39 2.615 @.72 1.000 1.ee 1.888 1.52 11.800 5.20 29.500 9.54 84.000 19.18 165.000 30.06 248.000 39.44 a^3/T2 1.0213 e.9868 1.eeee 0.9936 1.2298 e.9977 1. eeee 0.9977 .9975 The Law of Periods 60000 50000 40000 Cube of Semi-major axis (AU"3] 20.000 20000 10000 20000 30000 40000 50000 Square of Orbital Period year21 60000 1.0557245352884013e-19 G(Men)/(4p1*2) Bye! 5. Grading: - Algorithm in Pseudocode - Read data from file - Modular Programming opi (prec) readrile (planets, periods, distance) plot (num, denom) def thirdLaw (planets, distance, periods, LHS, num, denom): main() Correct Output - Graph - Readability/Comments TOTAL









