Computer science question (C++)

main.cpp

sort_simple.cpp

sort_template.cpp

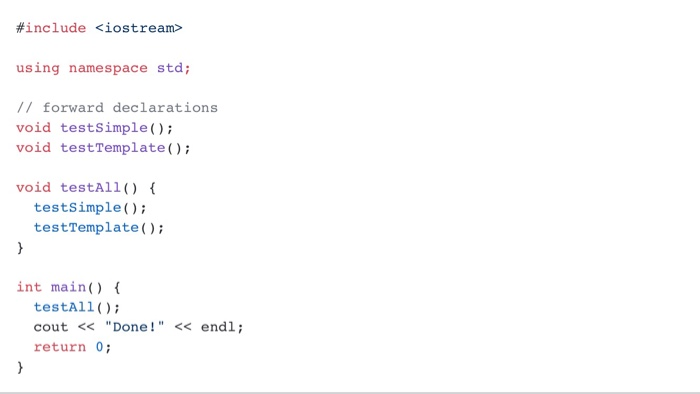
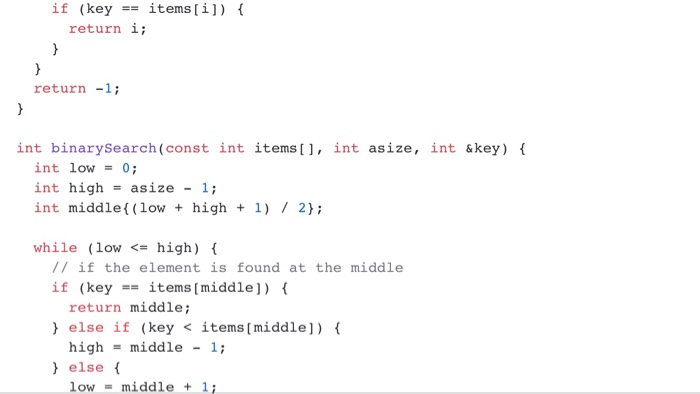
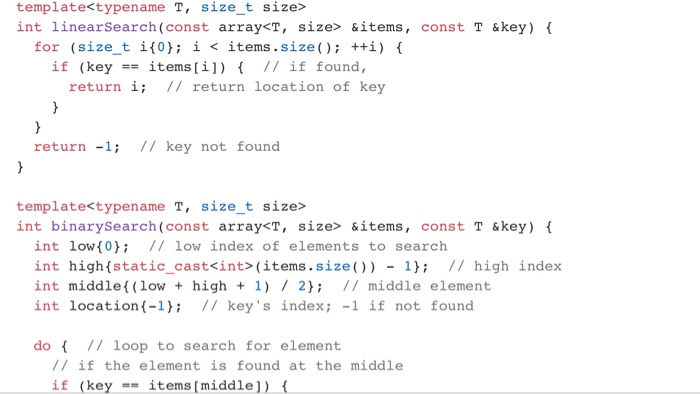
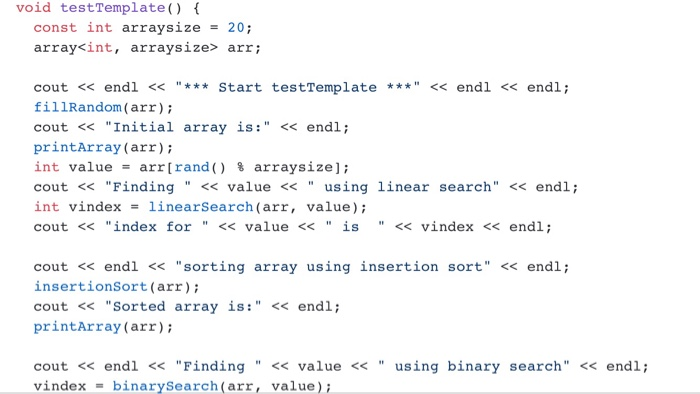
Bubble sort-another simple yet inefficient sorting technique. It's called bubble sort or sinking sort because smaller values gradually "bubble" their way to the top of the array (i.e., toward the first element) like air bubbles rising in water, while the larger values sink to the bottom (end) of the array. The technique uses nested loops to make several passes through the array. Each pass compares successive pairs of elements. If a pair is in increasing order (or the values are equal), the bubble sort leaves the values as they are. If a pair is in decreasing order, the bubble sort swaps their values in the array The first pass compares the first two element values of the array and swaps them if necessary It then compares the second and third element values in the array. The end of this pass compares the last two element values in the array and swaps them if necessary the largest value will be in the last eleent. After two passes, the largest two values will be in the last two elements. After one pass, Visualization of bubble sort can be found in https://visualgo.net/bn/sorting bubble.cpp: bubble sort implementation and a function 'testBubblethat demonstrates that your bubble sort works. Use builtin array rather than STL array for your implementation. main.cpp: calls testBubble0) README.md: Explanation of why bubble sort is an O(n2) algorithm Submit bubble.cpp, main.cpp and README.md (orREADME.txt) to Canvas. #include 0)&&(items [moveIndex - 1] > insert)) // shift element one slot to the right items [moveIndex]items [moveIndex -1 --moveIndex; items [move Index] = insert ; // place insert item back into array void selectionSort(int items[], int asize) f // loop over size 1 elements for (int i = 0; #include using namespace std; template void printArray (const array &items) for (int = 0; i void fil1Random(array &items) for (int i = 0; int linearSearch (const array &items, const T &key) f for (size t ifo); i int binarySearch(const array &items , const T &key) { int lowtO) low index of elements to search int high(static_cast(items. size))- 1) I/ high index int middlef (low + high + 1) / 2) 1/ middle element int location(-1): 1/ key's index; f not found do loop to search for element // if the element is found at the middle if (key-items [middle]) { locationmiddle; // location is the current middle ) else if (key void insertionSort(array &items)( /1 loop over the elements of the array for (size_t next(1; next 0)&&(items [moveIndex - 1] > insert)) ( // shift element one slot to the right items [moveIndex] items [move Index - 1]; --moveIndex; items [move Index) = insert ; // place insert item back into array template void selectionSort (array &items) // loop over size 1 elements for (size-t {0); i void merge (array &items, size t left, size t middlel, size t middle2, size t right) size t leftIndex(left); // index into left subarray size t rightIndex(middle2 17 index into right subarray sizet combinedIndex(left)i II index into temporary working array array combined; /I working array // merge arrays until reaching end of either while (leftIndex arr; cout