
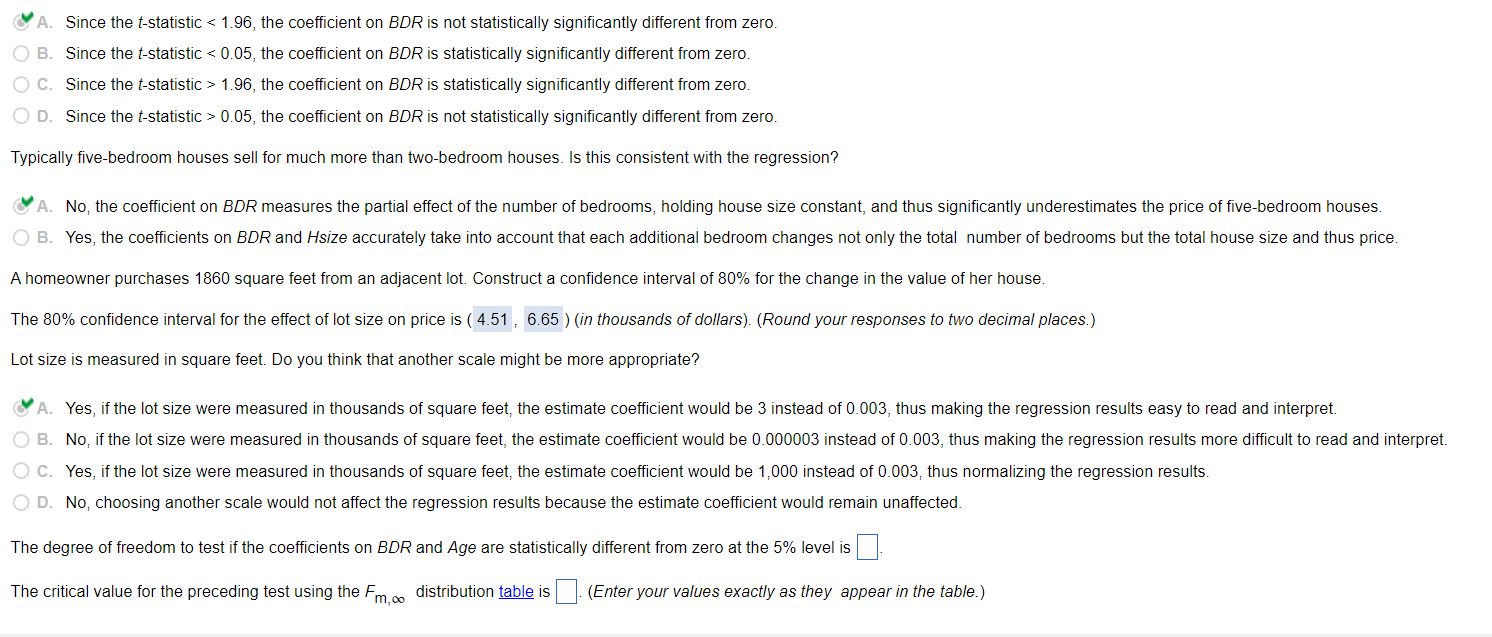
condition of the house is reported as "poor." An estimated regression yields: Price=110.9+0.451BDR+21.8Bath+0.145Hsize+0.003Lsize(22.2)(2.82)(8.31)(0.010)+0.084Age45.4Poor,R2=0.67,SER=38.6(0.289)(9.8) The t-statistic for the coefficient on BDR is (Round your response to three decimal places.) Is the coefficient on BDR statistically significantly different from zero? 'A. Since the t-statistic 1.96, the coefficient on BDR is statistically significantly different from zero. D. Since the t-statistic >0.05, the coefficient on BDR is not statistically significantly different from zero. Typically five-bedroom houses sell for much more than two-bedroom houses. Is this consistent with the regression? A homeowner purchases 1860 square feet from an adjacent lot. Construct a confidence interval of 80% for the change in the value of her house. A. Since the t-statistic 1.96, the coefficient on BDR is statistically significantly different from zero. D. Since the t-statistic >0.05, the coefficient on BDR is not statistically significantly different from zero. Typically five-bedroom houses sell for much more than two-bedroom houses. Is this consistent with the regression? A. No, the coefficient on BDR measures the partial effect of the number of bedrooms, holding house size constant, and thus significantly underestimates the price of five-bedroom houses. B. Yes, the coefficients on BDR and H size accurately take into account that each additional bedroom changes not only the total number of bedrooms but the total house size and thus price. A homeowner purchases 1860 square feet from an adjacent lot. Construct a confidence interval of 80% for the change in the value of her house. The 80% confidence interval for the effect of lot size on price is : I (in thousands of dollars). (Round your responses to two decimal places.) Lot size is measured in square feet. Do you think that another scale might be more appropriate? 'A. Yes, if the lot size were measured in thousands of square feet, the estimate coefficient would be 3 instead of 0.003, thus making the regression results easy to read and interpret. B. No, if the lot size were measured in thousands of square feet, the estimate coefficient would be 0.000003 instead of 0.003, thus making the regression results more difficult to read and interpret. C. Yes, if the lot size were measured in thousands of square feet, the estimate coefficient would be 1,000 instead of 0.003, thus normalizing the regression results. D. No, choosing another scale would not affect the regression results because the estimate coefficient would remain unaffected. The degree of freedom to test if the coefficients on BDR and Age are statistically different from zero at the 5% level is The critical value for the preceding test using the Fm, distribution is (Enter your values exactly as they appear in the table.) condition of the house is reported as "poor." An estimated regression yields: Price=110.9+0.451BDR+21.8Bath+0.145Hsize+0.003Lsize(22.2)(2.82)(8.31)(0.010)+0.084Age45.4Poor,R2=0.67,SER=38.6(0.289)(9.8) The t-statistic for the coefficient on BDR is (Round your response to three decimal places.) Is the coefficient on BDR statistically significantly different from zero? 'A. Since the t-statistic 1.96, the coefficient on BDR is statistically significantly different from zero. D. Since the t-statistic >0.05, the coefficient on BDR is not statistically significantly different from zero. Typically five-bedroom houses sell for much more than two-bedroom houses. Is this consistent with the regression? A homeowner purchases 1860 square feet from an adjacent lot. Construct a confidence interval of 80% for the change in the value of her house. A. Since the t-statistic 1.96, the coefficient on BDR is statistically significantly different from zero. D. Since the t-statistic >0.05, the coefficient on BDR is not statistically significantly different from zero. Typically five-bedroom houses sell for much more than two-bedroom houses. Is this consistent with the regression? A. No, the coefficient on BDR measures the partial effect of the number of bedrooms, holding house size constant, and thus significantly underestimates the price of five-bedroom houses. B. Yes, the coefficients on BDR and H size accurately take into account that each additional bedroom changes not only the total number of bedrooms but the total house size and thus price. A homeowner purchases 1860 square feet from an adjacent lot. Construct a confidence interval of 80% for the change in the value of her house. The 80% confidence interval for the effect of lot size on price is : I (in thousands of dollars). (Round your responses to two decimal places.) Lot size is measured in square feet. Do you think that another scale might be more appropriate? 'A. Yes, if the lot size were measured in thousands of square feet, the estimate coefficient would be 3 instead of 0.003, thus making the regression results easy to read and interpret. B. No, if the lot size were measured in thousands of square feet, the estimate coefficient would be 0.000003 instead of 0.003, thus making the regression results more difficult to read and interpret. C. Yes, if the lot size were measured in thousands of square feet, the estimate coefficient would be 1,000 instead of 0.003, thus normalizing the regression results. D. No, choosing another scale would not affect the regression results because the estimate coefficient would remain unaffected. The degree of freedom to test if the coefficients on BDR and Age are statistically different from zero at the 5% level is The critical value for the preceding test using the Fm, distribution is (Enter your values exactly as they appear in the table.)








