Consider a country which has 100 units of land, X, and 100 units of labor, L. It produces output under the production function Y=AX^L^. Suppose that =0.7, =0.3, and A=1. Create a table like the following in excel (this table has only one row; you will need to add more to answer the questions). MPL stands for the marginal product of labor, and APL for the marginal product of labor (which in lecture we also called y=Y/L)

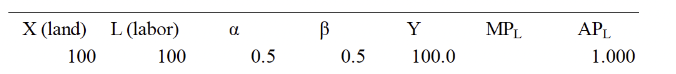
a) Show this production function exhibits constant returns to scale. b) Define the marginal product of labor (MPL) in your own words. c) Suppose that land is held fixed at 100, and labor is gradually added (keep X at 100 but add rows, with each row having one more worker). What is the marginal product of labor for the 101st worker? For the 110th? What is happening to the marginal product (MPL) of labor and the average product of labor (APL=y=Y/L) as the workers are added? How is this related to diminishing returns to labor? d) In class we saw the Malthusian model in graphical form. Is the table you prepared for the previous question consistent with the diagram presented in lecture? Which panel of the graph we used in class is your table most related to?