Consider a pure exchange economy without free disposal (i.e. agents cannot get rid of their goods) and with two commodities, j = 1, 2; and two traders i = I, II. Each trader i has the consumption set R 2 + and the endowments are given by e = (eI , eII ) = ((0, 8),(10, 0)). The preference relations of traders are given by the following utility functions uI (xI,1, xI,2) = min{2xI,1 + xI,2, 3xI,2}; uII (xII,1, xII,2) = min{3xII,1 + xII,2, xII,1 + 3xII,2}. A)Characterize the set of Weakly Pareto optimal allocations and Pareto optimal allocations and core allocations. B. Characterize the demand correspondences of these traders and identify the competitive equilibrium prices and allocations. If there is none, show why. C. Determine whether or not the conclusion of the first fundamental theorem of welfare economics holds. I.e. is every competitive equilibrium allocation Pareto optimal? How about the core? Is every competitive equilibrium allocation in the core? D. Determine whether or not the conclusion of the second fundamental theorem of welfare economics holds. I.e. can we support every Pareto optimal allocation as a competitive equilibrium allocation of an economy obtained via a feasible redistribution of the initial endowments?
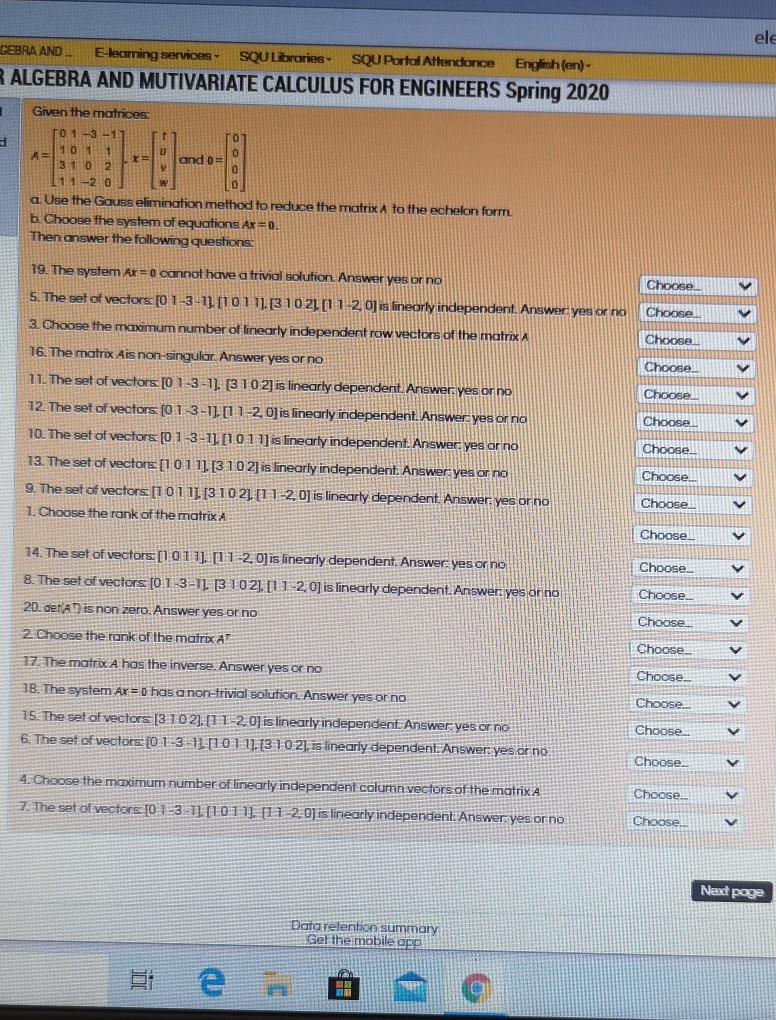
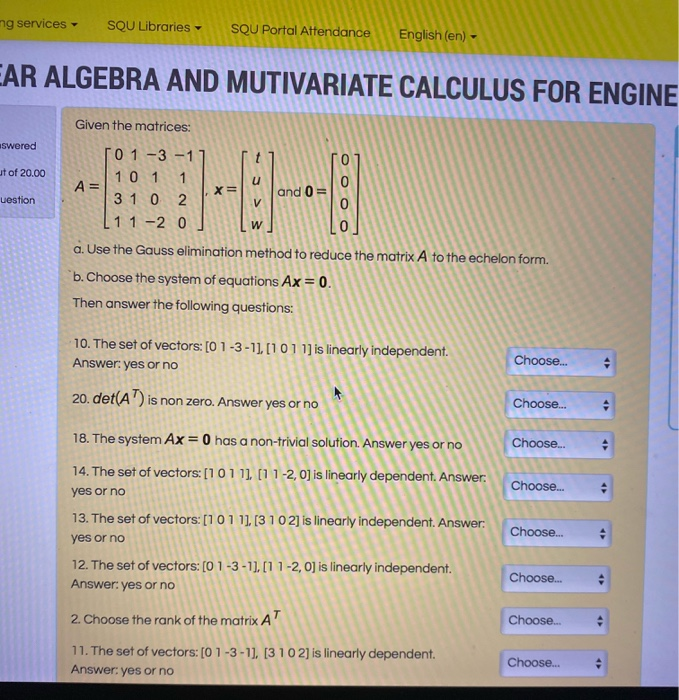
el GEBRA AND E-learning services - SQU Libraries - SQU Portal Attendance English (en)- ALGEBRA AND MUTIVARIATE CALCULUS FOR ENGINEERS Spring 2020 Given the matrices a. Use the Gauss elimination method to reduce the matrix A to the echelon form. b. Choose the system of equations Ar - 0. Then answer the following questions: 19. The system Ax = 0 cannot have a trivial solution. Answer yes or no Choose! 5. The set of vectors: [0 1 -3-1] [1 0 1 1]. [3 1 0 2) [1 1-2, 0] is linearly independent. Answer yes or no Choosel! V 3. Choose the maximum number of linearly independent row vectors of the matrix A Choose. 16. The matrix Ais non-singular. Answer yes or no Choose! 11. The set of vectors [0 1-3 -1], [3 1 0 2] is linearly dependent. Answer yes or no Choose!! 12. The set of vectors: [0 1-3 -1]. [1 1-2, O] is linearly independent. Answer yes or no Choosell 10. The set of vectors: [0 1 -3-1], [1 0 1 1] is linearly independent. Answer yes or no Choose! 13. The set of vectors [1 0 1 1], [3 1 0 2] is linearly independent. Answer: yes or no Choose!. 9. The set of vectors: [1 0 1 1) [3 10 21. [1 1-2. 0] is linearly dependent. Answer yes or no Choose! 1. Choose the rank of the matrix A Choose 14. The set of vectors [1 0 1 1], [1 1 -2. 0] is linearly dependent. Answer: yes or no Choose_. 8. The set of vectors [01 3-1]. [3 1 0 2], [1 1 2. 0] is linearly dependent. Answer yes or no Choose. 20. derA) is non zero. Answer yes or no Choose. 2. Choose the rank of the matrix A Choose 17. The matrix A has the inverse. Answer yes or no Choose. B. The system AX = 0 has a non-trivial solution. Answer yes or no Choose. 15. The set of vectors: [3 1:0 2], [1 1-2. 0] is linearly independent. Answer yes or no Choose. 6. The set of vectors: [0 1-3 -1] [10 1 1]. [3 1:0 21, is linearly dependent. Answer yes or no Choose 4. Choose the maximum number of linearly independent column vectors of the matrix A Choose 7. The set of vectors: [0.1 -3 1] [1:0 1 1]. [1 1 2. 0] is linearly independent. Answer yes or no Choose !!I Next page Data retention summary BGel the mobile appig services . SQU Libraries . SQU Portal Attendance English (en) . AR ALGEBRA AND MUTIVARIATE CALCULUS FOR ENGINE Given the matrices: swered it of 20.00 A = uestion 3 a. Use the Gauss elimination method to reduce the matrix A to the echelon form. b. Choose the system of equations Ax = 0. Then answer the following questions: 10. The set of vectors: [0 1 -3 -1], [1 0 1 1] is linearly independent. Choose.. Answer: yes or no 20. det(A ') is non zero. Answer yes or no Choose.. 18. The system Ax = 0 has a non-trivial solution. Answer yes or no Choose. 14. The set of vectors: [1 0 1 1], [1 1 -2, 0] is linearly dependent. Answer: Choose. yes or no 13. The set of vectors: [1 0 1 1], [3 10 2] is linearly independent. Answer: Choose. yes or no 12. The set of vectors: [0 1 -3 -1], [1 1 -2, 0] is linearly independent. Choose. Answer: yes or no 2. Choose the rank of the matrix A Choose. 11. The set of vectors: [0 1 -3 -1], [3 1 0 2] is linearly dependent. Choose. Answer: yes or no17. The average age of residents in a large residential retirement community is 69 years with standard deviation 5.8 years. A simple random sample of 100 residents is to be selected, and the sample mean age X of these residents is to be computed. We know the random variable Y has approximately a Normal distribution because of O a) the central limit theorem. 0 b) the law of large numbers. O c) the 68959937 rule. 0 d) the population we're sampling from has a Normal distribution