Consider a steady, laminar flow of an incompressible fluid through a channel of two infinitely long flat plates (in x and z directions), with the lower plate (at y = ?b) stationary and the upper plate (at y = b) moving at a constant velocity of V0. A known, constant pressure gradient p?is applied in the x direction. Neglect the effect of gravity. Let the dynamic viscosity of the fluid be ? and density be ?.

(a) Write down the component of the momentum equation you will use to solve for the velocity profile u(y). (b) It is argued that the flow is fully developed. Is it true? Explain (briefly) why or why not? (c) Is it safe to assume that the flow is two-dimensional? Why? What does it mean in terms of simplifying the equation? (d) Using appropriate assumptions, simplify the momentum equation clearly indicating which terms drop out and why. Clearly indicate the boundary conditions needed to solve the equation. (e) Solve for u in terms of ?, b, V0, and p?. (f) Find the and expression for the power needed to move the top plate. How does this power change if the viscosity doubles? How does it change if the top wall moves twice as fast? (g) Under what conditions (in terms of ?, b, V0, and p?) would the net mass flow rate be zero? Briefly explain why the flow rate is zero? Sketch how the velocity profile would look like under this condition.

CoursHeroTranscribedText

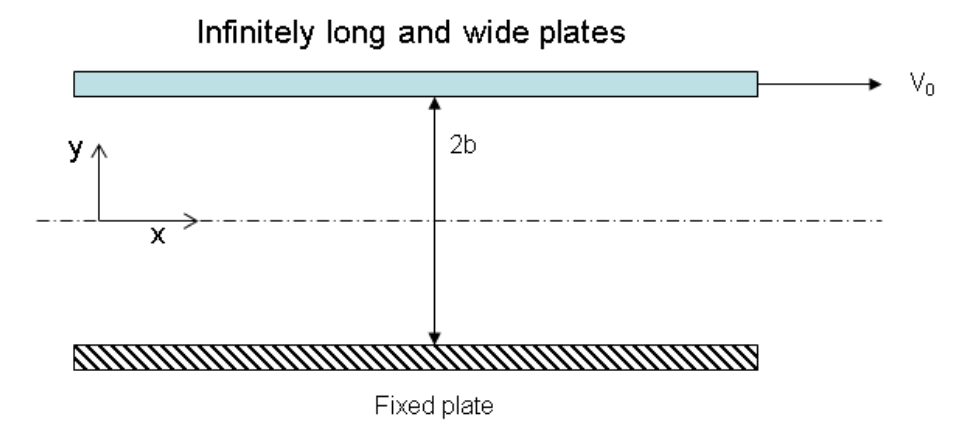
Infinitely long and wide plates 2b Fixed plate