 Consider a system that runs for a very long time (i.e., think about the limit when i and t ). Let the dashed lines in the illustration denote the lines whose slopes are given by N(t)/t and by D(t)/t as t . Answer the following questions: (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to . Recall that at steady state the average rate of process arrivals = the average rate of process departures. (2) Use the conclusion you made in (1) to prove Littles Law
Consider a system that runs for a very long time (i.e., think about the limit when i and t ). Let the dashed lines in the illustration denote the lines whose slopes are given by N(t)/t and by D(t)/t as t . Answer the following questions: (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to . Recall that at steady state the average rate of process arrivals = the average rate of process departures. (2) Use the conclusion you made in (1) to prove Littles Law
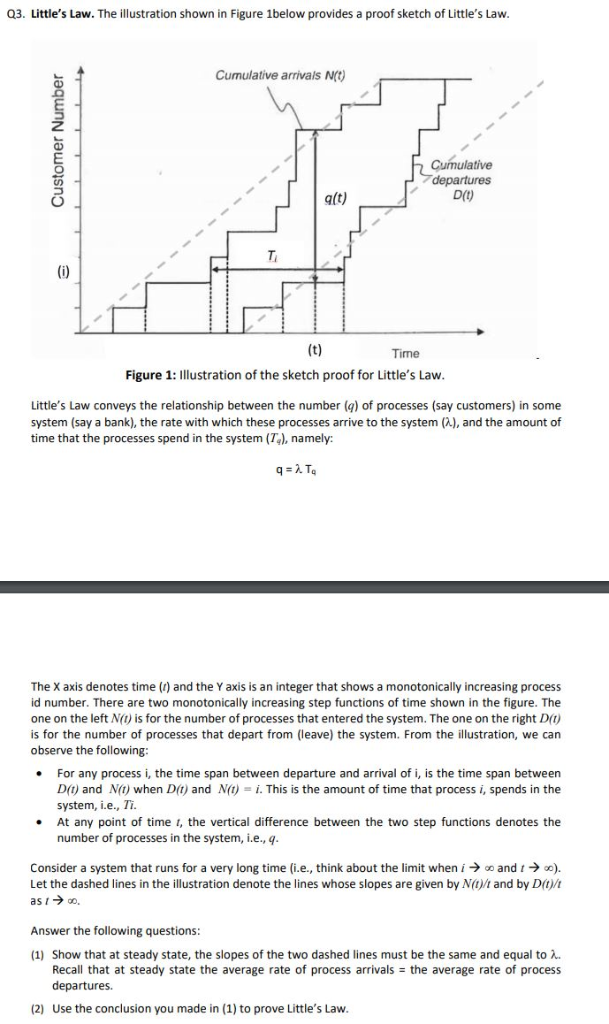
03. Little's Law. The illustration shown in Figure 1below provides a proof sketch of Little's Law Cumulative arrivals N Cumulative q(t) ime Figure 1: Illustration of the sketch proof for Little's Law Little's Law conveys the relationship between the number (q) of processes (say customers) in some system (say a bank), the rate with which these processes arrive to the system (A), and the amount of time that the processes spend in the system (Ta), namely: The X axis denotes time (r) and the Y axis is an integer that shows a monotonically increasing process id number. There are two monotonically increasing step functions of time shown in the figure. The one on the left N() is for the number of processes that entered the system. The one on the right Dt) is for the number of processes that depart from (leave) the system. From the illustration, we can observe the following For any process i, the time span between departure and arrival of i, is the time span between D(t) and Nt) when D(t) and N)-i. This is the amount of time that process i, spends in the system, i.e., Ti. At any point of time t, the vertical difference between the two step functions denotes the number of processes in the system, i.e., q Consider a system that runs for a very long time (i.e., think about the limit whenand). Let the dashed lines in the illustration denote the lines whose slopes are given by N()/t and by Dit)/ ast ->oo, Answer the following questions (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to Recall that at steady state the average rate of process arrivals the average rate of process departures. (2) Use the conclusion you made in (1) to prove Little's Law 03. Little's Law. The illustration shown in Figure 1below provides a proof sketch of Little's Law Cumulative arrivals N Cumulative q(t) ime Figure 1: Illustration of the sketch proof for Little's Law Little's Law conveys the relationship between the number (q) of processes (say customers) in some system (say a bank), the rate with which these processes arrive to the system (A), and the amount of time that the processes spend in the system (Ta), namely: The X axis denotes time (r) and the Y axis is an integer that shows a monotonically increasing process id number. There are two monotonically increasing step functions of time shown in the figure. The one on the left N() is for the number of processes that entered the system. The one on the right Dt) is for the number of processes that depart from (leave) the system. From the illustration, we can observe the following For any process i, the time span between departure and arrival of i, is the time span between D(t) and Nt) when D(t) and N)-i. This is the amount of time that process i, spends in the system, i.e., Ti. At any point of time t, the vertical difference between the two step functions denotes the number of processes in the system, i.e., q Consider a system that runs for a very long time (i.e., think about the limit whenand). Let the dashed lines in the illustration denote the lines whose slopes are given by N()/t and by Dit)/ ast ->oo, Answer the following questions (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to Recall that at steady state the average rate of process arrivals the average rate of process departures. (2) Use the conclusion you made in (1) to prove Little's Law
 Consider a system that runs for a very long time (i.e., think about the limit when i and t ). Let the dashed lines in the illustration denote the lines whose slopes are given by N(t)/t and by D(t)/t as t . Answer the following questions: (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to . Recall that at steady state the average rate of process arrivals = the average rate of process departures. (2) Use the conclusion you made in (1) to prove Littles Law
Consider a system that runs for a very long time (i.e., think about the limit when i and t ). Let the dashed lines in the illustration denote the lines whose slopes are given by N(t)/t and by D(t)/t as t . Answer the following questions: (1) Show that at steady state, the slopes of the two dashed lines must be the same and equal to . Recall that at steady state the average rate of process arrivals = the average rate of process departures. (2) Use the conclusion you made in (1) to prove Littles Law





